Интерполирующие цифровые фильтры.

Интерполяцией называется увеличение количества отсчетов сигнала в единицу времени. Отношение количества новых отсчетов сигнала в единицу времени по отношению к предыдущему количеству отсчетов сигнала называется коэффициентом интерполяции. Обычно это отношение выбирается целым числом.

При увеличении частоты отсчетов сигнала в соответствии с теоремой Котельникова расширяется полоса частот, описываемых этими отсчетами. Это означает, что в новую полосу частот попадает несколько частотных образов первоначального варианта сигнала. При интерполяции необходимо выбрать нужный частотный образ. Обычно выбирается полоса частот от 0 до f_в.

Задача выбора необходимого частотного образа решается при помощи цифрового фильтра. Такой фильтр называется интерполирующим. Именно этот фильтр вычисляет значения сигнала в точках между первоначальными отсчетами сигнала.

Рассмотрим пример первоначального представления сигнала во временной области. Пример временной реализации сигнала приведен на рисунке 11.2.6

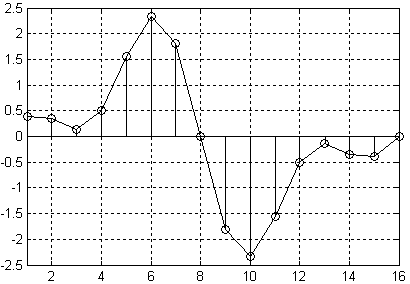
Рисунок 11.2.6 Пример временной реализации сигнала.

На данном рисунке отсчеты сигнала обозначены кружочками, а для того чтобы легче было видеть форму сигнала, они соединены прямыми линиями. При интерполяции сигнала требуется увеличить количество его отсчетов в единицу времени. Новые отсчеты сигнала заполняются нулевыми значениями, как это показано на рисунке 11.2.7

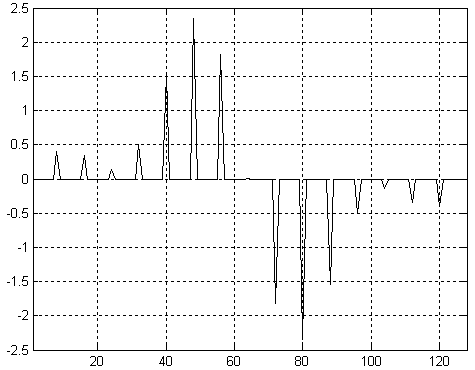
Рисунок 11.2.7 Сигнал на входе интерполирующего фильтра.

Спектр этого же сигнала приведен на рисунке 11.2.8. На графике четко виден повторяющийся характер спектра. Теперь для того, чтобы осуществить интерполяцию сигнала необходимо подавить нежелательные спектральные компоненты сигнала.

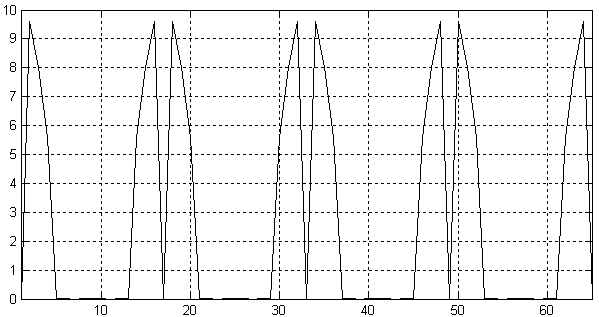
Рисунок 11.2.8. Спектр сигнала, приведенного на рисунке 11.2.7.

Подавим все высокочастотные составляющие спектра сигнала при помощи цифрового фильтра. Для этого зададимся уровнем подавления этих составляющих спектра –75 дБ. Такие параметры можно реализовать цифровым фильтром со 128 отводами. Получившаяся амплитудно-частотная характеристика интерполирующего КИХ-фильтра, структурная схема которого рассматривалась нами ранее (рисунок 11.2.7), c шестнадцатиразрядными коэффициентами.

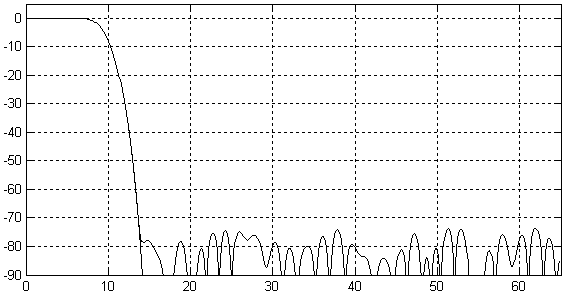
Рисунок 11.2.9 Амплитудно-частотная характеристика интерполирующего фильтра.

В полосе пропускания такой фильтр обеспечивает неравномерность коэффициента передачи на уровне 0,001 дБ. Таким образом, учитывая, что фильтр с конечной импульсной характеристикой обладает линейной фазовой характеристикой, он практически не вносит искажений в исходный сигнал.

При прохождении через разработанный фильтр сигнал принимает вид, приведенный на рисунке 11.2.10 Сигнал на выходе фильтра будет задержан на групповое время задержки фильтра. Для КИХ-фильтра это время равно тактовой частоте умноженной на половину количества отводов фильтра.

На рисунке 11.2.10 приведено 128 временных отсчетов сигнала. Они практически сливаются друг с другом, поэтому отдельные отсчеты не выделяются кружочками, как это было сделано на рисунке 11.2.6. Как видно из приведенного на рисунке графика сигнал на выходе фильтра практически не отличается от исходного (существовавшего до дискретизации) сигнала.

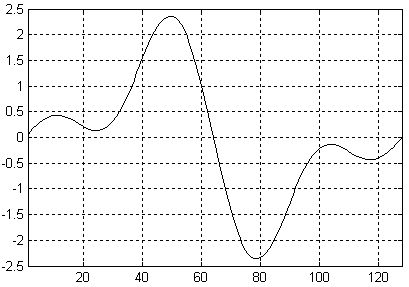
Рисунок 11.2.10 Сигнал на выходе интерполирующего фильтра.

Так как реальный фильтр всегда имеет конечную крутизну ската своей амплитудно-частотной характеристики, то полоса частот сигнала, подлежащего интерполяции всегда должна быть меньше половины частоты дискретизации. Только в этом случае интерполяция сигнала может быть выполнена без искажений.

Теперь рассмотрим, как будет выглядеть этот же сигнал, если выделить первый образ исходного сигнала. Получившийся сигнал приведен на рисунке 11.2.11. Так как в этом случае номера отсчетов сигнала не нормированы относительно начала координат, то на этом же рисунке приведен низкочастотный образ сигнала.

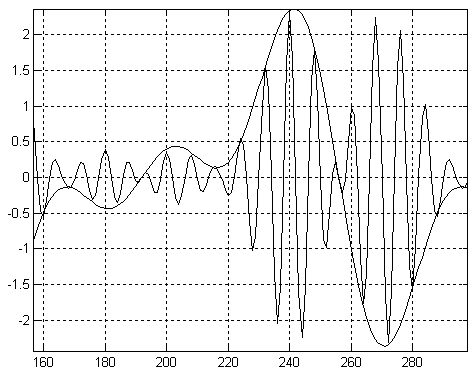
Рисунок 11.2.11 Сигнал на выходе интерполирующего фильтра.

На рисунке отчетливо видно, что исходные значения сигнала совпадают как в низкочастотном, так и в первом образе сигнала. В момент пересечения нулевого значения фаза несущей частоты первого образа меняет свой знак. Точно так же вели бы себя и второй и третий образ сигнала. Отличие заключается только в значении несущей частоты.

Применение для формирования несущей частоты высокочастотных образов первоначального сигнала неудобно, так как в этом случае можно реализовать всего несколько фиксированных частот. Намного удобнее для переноса спектра исходного сигнала на несущую частоту использовать схему квадратурного модулятора. Эта схема позволяет переносить спектр исходного сигнала на любую частоту, не превышающую половину частоты дискретизации.

Интерполяция обычно производится в несколько этапов. Первые два этапа обычно обеспечивают увеличение скорости отсчетов сигнала в два раза каждый. Это связано с тем, что первоначально почти вся полоса частот от 0 до fд/2 занята полезным сигналом, т.е. полезный сигнал и его высокочастотные образы находятся близко друг от друга. В результате от интерполирующего фильтра требуется высокая крутизна ската амплитудно-частотной характеристики и для его реализации требуется большое количество отводов и коэффициентов.

После выполнения этих первых двух этапов интерполяции полезный сигнал занимает только 25% полосы частот. В результате требования к избирательности фильтра уменьшаются, а значит, последующий интерполирующий фильтр может обеспечить больший коэффициент интерполяции.

Здесь я хотел бы подчеркнуть, что промежуточные отсчеты должны быть заполнены именно нулями. Если их заполнить другими значениями, например повторениями предыдущего отсчета сигнала, то уровень высокочастотных составляющих спектра значительно уменьшится. Однако при этом будет искажен и сигнал в основной полосе. Более того, станет невозможным применять в качестве фильтра-интерполятора фильтры Найквиста, так как исходные значения отсчетов сигнала будут искажены.

В заключение я хотел бы привести структурную схему прямого синтеза, на вход которой можно подавать цифровой поток с частотой отсчетов, в несколько раз ниже по отношению к требующейся для формирования выходного радиосигнала. Эта схема приведена на рисунке 11.2.12.

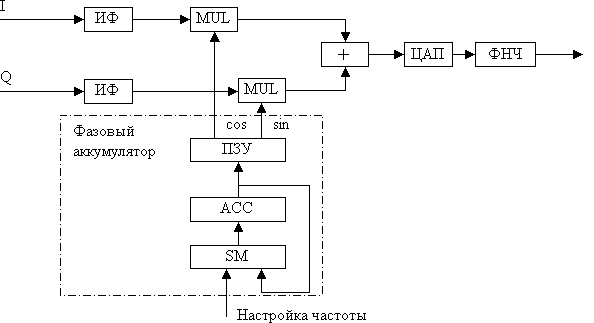
Рисунок 11.2.12. Структурная схема квадратурного модулятора с низкоскоростным потоком квадратурных сигналов.