Умножители

Умножение в двоичном виде производится подобно умножению в десятичной системе счисления. Как мы это помним из школьного курса, легче всего осуществлять умножение в столбик. При этом потребуется перемножить каждый разряд множимого на соответствующий разряд множителя, а затем просуммировать полученные частные произведения.

Рассмотрим в качестве примера умножение двух четырёхразрядных двоичных чисел. Пусть требуется умножить число 1011₂ (11₁₀) на число 1101₂ (13₁₀). Мы в результате умножения ожидаем получить число 10001111₂(143₁₀). Выполним операцию умножения в столбик, как это показано на рисунке 11.12

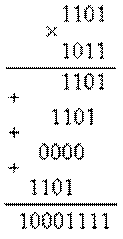
Рисунок 11.1.12 Выполнение операции умножения в столбик

Для формирования произведения требуется вычислить четыре частичных произведения. Обратите внимание, что в двоичной арифметике требуется выполнять умножение только на числа 0 и 1. Это означает, что нужно либо суммировать множимое к сумме остальных частичных произведений, либо нет. Таким образом, для формирования частичного произведения можно воспользоваться логическими элементами "2И".

Для формирования частичного произведения, кроме операции умножения на один разряд, требуется осуществлять его сдвиг влево на число разрядов, соответствующее весу разряда множителя. Сдвиг можно осуществить простым соединением соответствующих разрядов частичных произведений к необходимым разрядам двоичного сумматора.

Для того чтобы принципиальная схема умножителя была похожа на алгоритм двоичного умножения, приведённый на рисунке 11.1.12, используем условно-графические изображения микросхем, где входы расположены сверху, а выходы снизу. В полном соответствии с алгоритмом умножения в столбик нам потребуются тричетырёхразрядных сумматора.

Принципиальная схема умножителя, реализующая алгоритм двоичного умножения в столбик, приведена на рисунке 11.1.13. Формирование частичных произведений в этой схеме осуществляют микросхемы D1, D3, D5, D7. В этих микросхемах содержится сразу четыре логических элемента "2И".

Сумматор, выполненный на микросхеме D6, суммирует первое и второе частные произведения. При этом младший разряд первого частного произведения не нуждается в суммировании (см. рисунок 11.1.12). Поэтому он подаётся на выход умножителя непосредственно (разряд M0). Второе частное произведение должно быть сдвинуто на один разряд. Это осуществляется тем, что младший разряд выходного числа сумматора D6 соединяется со вторым разрядом произведения (M1). Но тогда первое частное произведение необходимо сдвинуть на один разряд по отношению ко второму частному произведению! Это выполняется тем, что младший разряд группы входов A соединяется с первым разрядом частного произведения, первый разряд группы входов A соединяется со вторым разрядом частного произведения, и т.д. Однако старший разряд группы входов A не с чем соединять! Вспомним, что если добавить к числу слева ноль, то значение числа не изменится, поэтому мы можем этот разряд соединить с общим проводом схемы.

Точно таким же образом осуществляется суммирование третьего и четвёртого частного произведения. Это суммирование выполняют микросхемы D4 и D2 соответственно. Отличие заключается только в том, что здесь не нужно задумываться о старшем разряде предыдущей суммы, ведь предыдущая микросхема сумматора формирует сигнал переноса.

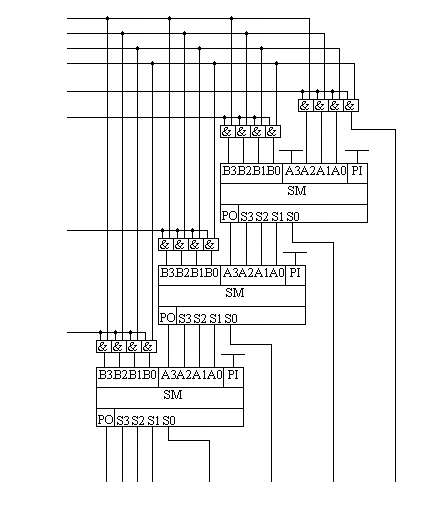
Рисунок 11.1.13 Схема матричного умножителя 4*4

Если внимательно посмотреть на схему умножителя, то можно увидеть, что она образует матрицу, сформированную проводниками, по которым передаются разряды числа A и числа B. В точках пересечения этих проводников находятся логические элементы “2И”. Именно по этой причине умножители, реализованные по данной схеме, получили название матричных умножителей.

Скорость работы схемы, приведенной на рисунке 11.1.13, определяется максимальным временем распространения сигнала. Это цепь D7, D6, D4, D2. Время работы схемы можно сократить, если сумматоры располагать не последовательно друг за другом, как это предполагается алгоритмом, приведенным на рис. 11.1.12, а суммировать частичные произведения попарно, затем суммировать пары частичных произведений и т.д. В этом случае время выполнения операции умножения значительно сократится.

Особенно заметен выигрыш в быстродействии при построении многоразрядных умножителей, однако ничего не бывает бесплатно. В обмен на быстродействие придётся заплатить увеличением разрядности сумматоров, а значит сложностью схемы. Если сумматоры частных произведений останутся той же разрядности, что и ранее, то разрядность сумматоров пар частичных произведений должна быть увеличена на единицу. Разрядность сумматоров четвёрок частичных произведений будет на два разряда больше разрядности сумматоров частичных произведений и т.д.

Глава 3