Мощность, развиваемая источником тока во всей цепи, называется полной мощностью.
Она определяется по формуле
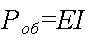
где Pоб-полная мощность, развиваемая источником тока во всей цепи, вт;
Е- э. д. с. источника, в;
I-величина тока в цепи, а.
Заменяя в выражении полной мощности величину э. д. с. через напряжения на участках цепи, получим
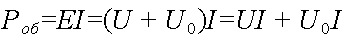
Величина UI соответствует мощности, развиваемой на внешнем участке цепи (нагрузке), и называется полезной мощностьюPпол=UI.
Величина UoI соответствует мощности, бесполезно расходуемой внутри источника, Ее называют мощностью потерь Po=UoI.
Таким образом, полная мощность равна сумме полезной мощности и мощности потерь Pоб=Pпол+P0.
Отношение полезной мощности к полной мощности, развиваемой источником, называется коэффициентом полезного действия, сокращенно к. п. д.,и обозначается η.
Из определения следует
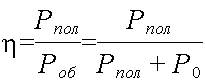
При любых условиях коэффициент полезного действия η ≤ 1.
Если выразить мощности через величину тока и сопротивления участков цепи, получим

Таким образом, к. п. д. зависит от соотношения между внутренним сопротивлением источника и сопротивлением потребителя.
Обычно электрический к. п. д. принято выражать в процентах.
34. На неоднородном участке цепи действуют как электрические, так и сторонние силы.
Напряжение на участке цепи равно отношению алгебраической суммы работ электростатических и сторонних сил по переносу заряда q на данном участке к переносимому заряду:

Полное сопротивление участка:

Закон Ома для неоднородного участка цепи:
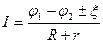
Правило знаков: перед I берут знак «+» , если направление тока совпадает с направлением от 1 к 2, и наоборот.
Все электрические цепи, по которым протекает постоянный электрический ток, должны быть замкнутыми
Закон Ома для полной(замкнутой) цепи:
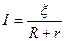
Напряжение на зажимах источника равно напряжению на резисторе R:
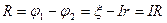
35. Первый закон Кирхгофа:алгебраическая сумма токов, сходящихся в узле, равна нулю:
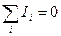
Второй закон Кирхгофа:
В любом замкнутом контуре, произвольно выбранном в разветвленной цепи постоянного тока, сумма падений напряжения в ветвях контура равна алгебраической сумме ЭДС в этом контуре:
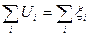
Где 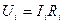 - падение напряжения на резисторе,
- падение напряжения на резисторе, 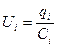 - падение напряжения на конденсаторе
- падение напряжения на конденсаторе
36.Последовательное соединение источников – это соединение, при котором один полюс промежуточного источника соединяется с полюсом произвольного знака предыдущего, а второй полюс промежуточного источника соединяется с полюсом последующего источника.
ЭДС батареи равна разности потенциалов на ее зажимах:
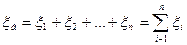
В зависимости от полярности ЭДС 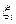 войдет в сумму с тем или иным знаком.
войдет в сумму с тем или иным знаком.
Если такую батарею замкнуть на резистор, то в цепи будет сила тока:
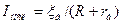
Где R – внешнее сопротивление, а сопротивление батареи - 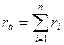
 - арифметическая сумма.
- арифметическая сумма.
Параллельное соединение источников – такое, при котором одни полюса соединяют в один узел, другие в другой. При таком соединении внутри даже отключенной от нагрузки батареи могут протекать точки, и разность потенциалов на ее полюсах рассчитывается по правилам Кирхгофа.
37. Носителями тока в металлах служат свободные электроны. Это подтверждалось рядом классических опытов.
В опыте К.Рикке (1901 г.)электрический ток в течение года пропускался через три последовательно соединенных металлических цилиндра (Cu, Al, Cu) с отшлифованными торцами одинакового радиуса. Общий заряд, прошедший через цилиндры, равнялся 3.5×106 Кл. Проведенное после этого взвешивание показало, что вес цилиндров не изменился, также не было обнаружено проникновения одного металла в другой. Следовательно, перенос заряда осуществлялся не ионами, а общими для всех металлов частицами - электронами.
Для подтверждения этого положения необходимо было определить знак и величину удельного заряда q/m (заряда единицы массы)носителей тока. Идея опытов и их качественное воплощение принадлежит российскими физиками Л.Мандельштаму и Н.Папалески (1913 г.). Если движущийся поступательно проводник резко остановить, то, подключенный к нему гальванометр зафиксирует кратковременный ток. Это объясняется тем, что носители тока не связаны жестко с кристаллической решеткой и при торможении продолжают двигаться по инерции. По направлению тока гальванометра было определено, что знак заряда носителя тока -отрицательный. Согласно численному расчету, удельный заряд носителя тока оказался приблизительно равным удельному заряду электрона. К таким же результатам привели опыты Ч.Стюарта и Т.Толмена (1916 г.), в которых быстрые крутильные колебания катушки, соединенной с чувствительным гальванометром, создавали переменный электрический ток. Таким образом, было доказано, что носителями электрического тока в металлах являются свободные электроны.
38.Основные положения КЭТ.
1) металлический проводник рассматривается как совокупность ионов находящихся в узлах кристаллической решетки и свободных электронов, т.е. бывших валентных атомов потерявших с ними связь и превративших их в полярные ионы
2) свободные электроны находятся в состоянии беспрерывного хаотичного движения, подобно молекулам идеального газа
3) свободные электроны рассматривают как некий газ, подобный идеальному газу молекулярной физики
39.Пусть в металлическом проводнике существует электрическое поле напряженностью Е=const. Co стороны поля заряд е испытывает действие силы F=eE и приобретает ускорение а=F/m=еЕ/т. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость
vmax= еE<t>.
где <t>—среднее время между двумя последовательными соударениями электрона с ионами решетки.
Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона
<v>=(vmax+0)/2=eE<t>/(2m). (103.1)
Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время <t> свободного пробега определяется средней длиной свободного пробега <l> и средней скоростью движения электронов относительно кристаллической решетки проводника, равной <u>+(v) (<u>—средняя скорость теплового движения электронов). В §102 было показано, что (v)<< <u>, поэтому
<t>=<l>/<u>.
Подставив значение <t>в формулу (103.1), получим
<v>=eE<l>/(2m<u>).
Плотность тока в металлическом проводнике, по (96.1),

откуда видно, что плотность тока пропорциональна напряженности поля,
т. е. получили закон Ома в дифференциальной форме (ср. с (98.4)). Коэффициент пропорциональности между j и Е есть не что иное, как удельная проводимость материала
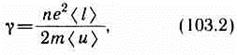
которая тем больше, чем больше концентрация свободных электронов и средняя длина их свободного пробега.
Закон Джоуля-Ленца
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля
Математически может быть выражен в следующей форме:
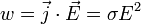
где 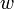 — мощность выделения тепла в единице объёма,
— мощность выделения тепла в единице объёма, 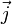 — плотность электрического тока,
— плотность электрического тока, 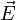 — напряжённость электрического поля, σ — проводимость среды.
— напряжённость электрического поля, σ — проводимость среды.
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка
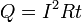
40. Металлы обладают как большой электропроводностью, так и высокой теплопроводностью. Это объясняется тем, что носителями тока и теплоты в металлах являются одни и те же частицы — свободные электроны, которые, перемещаясь в металле, переносят не только электрический заряд, но и присущую им энергию хаотического теплового движения, т. е. осуществляют перенос теплоты.
Видеманом и Францем в 1853 г. экспериментально установлен закон, согласно которому отношение теплопроводности (l) к удельной проводимости (g) для всех металлов при одной и той же температуре одинаково и увеличивается пропорционально термодинамической температуре:
χ/g=аT,
где а — постоянная, не зависящая от рода металла.
Элементарная классическая теория электропроводности металлов позволила найти значение а: а=3(k/e)2, где k — постоянная Больцмана.
Успехи:
- Объяснение электрического сопротивления R
- Объяснение законов Ома и Джоуля Ленца
- Качественное объяснение закона Видемана Франца
41. Работой выхода Aвых называется минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. Свободные электроны, выходя за пределы кристаллической решетки металла, образуют вокруг него электронное облако. Между ним и кристаллической решеткой создается электрическое поле, препятствующее дальнейшему выходу электронов из металла. Для того, чтобы электрон покинул металл, он должен обладать достаточной энергией для преодоления этого поля. Скорости электронов в системе различны. Электрону с меньшей энергией надо сообщить большую порцию энергии, чем электрону с меньшей энергией, для того чтобы они покинули металл. Работа выхода Aвых зависит только то химического состава металла и от состояния его поверхности.
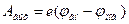
Контактная разность потенциалов — это разность потенциалов, возникающая при соприкосновении двух различных проводников, находящихся при одинаковой температуре.При соприкосновении двух проводников с разными работами выхода на проводниках появляются электрические заряды. А между их свободными концами возникает разность потенциалов. Разность потенциалов между точками находящимися вне проводников, в близи их поверхности называется контактной разностью потенциалов[1].
Законы Вольты:
- на контакте двух разных металлов возникает разность потенциалов, которая зависит от химической природы и от температуры спаев
- разность потенциалов на концах последовательно соединенных проводников не зависит от промежуточных проводников и равна разности потенциалов, возникающей при соединении крайних проводников при той же температуре
Согласно второму закону Вольта, в замкнутой цепи, состоящей из нескольких металлов, находящихся при одинаковой температуре, э.д.с. не возникает, т. е. не происходит возбуждения электрического тока. Однако если температура контактов не одинакова, то в цепи возникает электрический ток, называемый термоэлектрическим.Явление возбуждения термоэлектрического тока (явление Зеебека),а также тесно связанные с ним явления Пельтье и Томсонаназываются термоэлектрическими явлениями.
Эффект Зеебека состоит в том, что в замкнутой цепи, состоящей из разнородных проводников, возникает термо-ЭДС, если места контактов поддерживают при разных температурах. Цепь, которая состоит только из двух различных проводников называется термоэлементом или термопарой.
Величина возникающей термоэдс зависит только от материала проводников и температур горячего ( 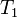 ) и холодного (
) и холодного ( 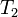 ) контактов.
) контактов.
В небольшом интервале температур термоэдс 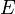 можно считать пропорциональной разности температур:
можно считать пропорциональной разности температур:
 , где
, где 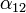 — термоэлектрическая способность пары (или коэффициент термоэдс).
— термоэлектрическая способность пары (или коэффициент термоэдс).
В простейшем случае коэффициент термоэдс определяется только материалами проводников, однако строго говоря, он зависит и от температуры, и в некоторых случаях с изменением температуры 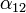 меняет знак.
меняет знак.
Эффект Пельтье — термоэлектрическое явление, при котором происходит выделение или поглощение тепла при прохождении электрического тока в месте контакта (спая) двух разнородных проводников. Величина выделяемого тепла и его знак зависят от вида контактирующих веществ, направления и силы протекающего электрического тока:
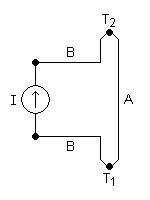
Q = ПАBIt = (ПB-ПA)It, где
Q — количество выделенного или поглощённого тепла;
I — сила тока;
t — время протекания тока;
П — коэффициент Пельтье, который связан с коэффициентом термо-ЭДС α вторым соотношением Томсона [1] П = αT, где Т — абсолютная температура в K.
44.Итак, по двум длинным прямым параллельным проводникам, находящимся на расстоянии R друг от друга (которое во много, раз в 15 меньше длин проводников), протекают постоянные токи I1, I2.
В соответствии с полевой теорией взаимодействие проводников объясняется следующим образом: электрический ток в первом проводнике создает магнитное поле, которое взаимодействует с электрическим током во втором проводнике. Чтобы объяснить возникновение силы, действующей на первый проводник, необходимо проводники «поменять ролями»: второй создает поле, которое действует на первый. Повращайте мысленно правый винт, покрутите левой рукой (или воспользуйтесь векторным произведением) и убедитесь, что при токах текущих в одном направлении, проводники притягиваются, а при токах, текущих в противоположных направлениях, проводники отталкиваются [1].
Таким образом, сила, действующая на участок длиной Δl второго проводника, есть сила Ампера, она равна
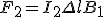 , (1)
, (1)
где B1 - индукции магнитного поля, создаваемого первым проводником. При записи этой формулы учтено, что вектор индукции 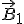 перпендикулярен второму проводнику.
перпендикулярен второму проводнику.
Силой Ампера называют силу, действующую на проводник длиной l, по которому течет ток I в магнитном поле с индукцией 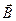 :
:
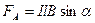 ,
,
Где 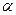 - угол между направлением вектора магнитной индукции
- угол между направлением вектора магнитной индукции 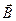 и направлением тока
и направлением тока
СГСМ
В СГСМ магнитная постоянная µ0 безразмерна и равна 1, а электрическая постоянная ε0 = 1/с2 (размерность: с2/см2). В этой системе нефизические коэффициенты отсутствуют в формуле закона Ампера для силы, действующей на единицу длины l каждого из двух бесконечно длинных параллельных прямолинейных токов в вакууме: F = 2I1I2l/d, где d — расстояние между токами. В результате единица силы тока должна быть выбрана как квадратный корень из единицы силы (дина1/2). Из выбранной таким образом единицы силы тока (иногда называемой абампером, размерность: см1/2г1/2с−1) выводятся определения производных единиц (заряда, напряжения, сопротивления и т. п.).
Сила тока
СИ 1 а
СГСМ 10 а
СГСЭ 10/с а
Электрическое напряжение
СИ 1 в
СГСМ 10-8 в
СГСЭ 10-8×с в
Электрическое сопротивление
СИ 1 ом
СГСМ 10-9 ом
СГСЭ 10-9×с2 ом
Электрическая ёмкость
СИ 1 Ф
СГСМ 109 ф
СГСЭ 109/с2 ф
45. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2]
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.
Основной силовой характеристикой магнитного поля является вектор магнитной индукции 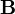 (вектор индукции магнитного поля)
(вектор индукции магнитного поля)
Магни́тная инду́кция 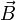 — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой 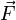 магнитное поле действует на заряд
магнитное поле действует на заряд 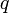 , движущийся со скоростью
, движущийся со скоростью 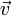 .
.
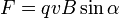
46. Магнитная проницаемость среды — это физическая величина, показывающая, во сколько раз модуль магнитной индукции В поля в однородной среде отличается от модуля магнитной индукции B0 в той же точке поля в вакууме:
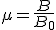
Напряженность магнитного поля векторная величина Н, являющаяся количеств. хар-кой магн. поля. Н. м. п. не зависит от магн. св-в среды. В вакууме Н. м. п. совпадает с магнитной индукцией В, численно
H=B в СГС системе единиц и
H=В/m0 в Международной системе единиц (СИ), m0 — магнитная постоянная.
В среде Н. м. п. Н определяет тот вклад в магн. индукцию B, к-рый дают внеш. источники поля:
Н=В-4pJ (в системе ед. СГС) или
H=(B/m0)-J (в СИ),
где J— намагниченность среды.
Величина B в системе единиц СИ измеряется в теслах, в системе СГС в гауссах.
Напряженность H измеряется в амперах на метр (А/м) в системе СИ и в эрстедах в СГС.
· 1 Тл = 10 000 гаусс (единица СГС)
1 эрстед = 1000/(4π) A/м ≈ 79,5774715 А/м.
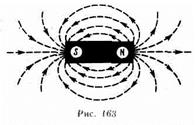
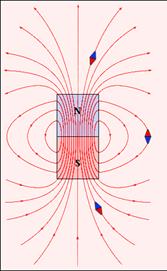
47.Силовые линии – линии, касательные которых к каждой точке совпадает с движением
Линии В всегда замкнуты, поэтому магнитное поле является вихревым

Магнитным потоком Ф через некоторую поверхность S называется скалярная величина, равная произведению модуля вектора магнитной индукции на площадь этой поверхности и косинус угла между нормалью n к ней и направлением вектора магнитной индукции B:Ф=|B|Scos α
Закон Гаусса для магнитного поля — поток магнитной индукции через замкнутую поверхность равен нулю
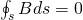
Теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым..
Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей.
48. Магнитное поле действует с некоторой силой на любой проводник с током,
находящийся в нем.
Если проводник, по которому протекает электрический ток подвесить в магнитном поле, например, между полюсами магнита, то магнитное поле будет действовать на проводник с некоторой силой и отклонять его.
 Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента дли-
Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента дли-
ной dl проводника на магнитную индукцию В:
dF = I[dl, В].
Сила Ампера: 
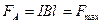
49.На рамку с током I, помещенную во внешнее однородное магнитное поле с индукцией 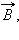 действует момент сил
действует момент сил  Момент сил выражается соотношением:
Момент сил выражается соотношением:
| M = I S B sin α = pmB sin α , |
где S – площадь рамки, α – угол между нормалью 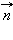 к плоскости рамки и вектором
к плоскости рамки и вектором 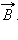 Векторная величина
Векторная величина 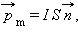 где
где 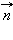 – единичный вектор нормали, называется магнитным моментом рамки. Направление вектора
– единичный вектор нормали, называется магнитным моментом рамки. Направление вектора  связано с направлением тока в рамке правилом правого винта.
связано с направлением тока в рамке правилом правого винта.
Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток.
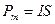
ДИПОЛЬ МАГНИТНЫЙ (от греч. di-, в сложных словах-дважды, двойной и polos - полюс)-аналог диполя электрического, к-рый можно представлять себе как два точечных магн. заряда 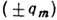 , расположенных на расстоянии l друг от друга. Характеризуется дипольным моментом, равным по величине
, расположенных на расстоянии l друг от друга. Характеризуется дипольным моментом, равным по величине 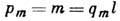
50.Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид.
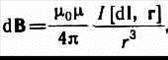 где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r — радиус-вектор,
где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r — радиус-вектор, 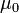 - константа (магнитная проницаемость вакуума)
- константа (магнитная проницаемость вакуума)
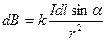
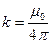
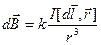
51. . Магнитное поле прямого тока —тока, текущего по тонкому прямому про-
воду бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол а (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что
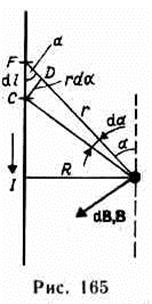
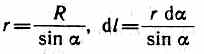
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
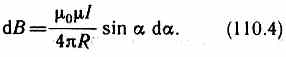
Так как угол а для всех элементов прямого тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4),
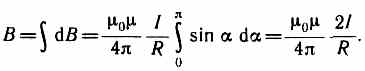
Следовательно, магнитная индукция поля прямого тока:
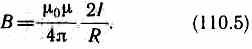
Дата добавления: 2014-12-24; просмотров: 5801;
