Процесс распространения ЭМЭ в длинных линиях

Двухпроводные линии представляют собой электрические цепи с распределенными параметрами. В отличие от цепей с сосредоточенными параметрами, в которых индуктивность сосредоточена в катушках, а емкость – в конденсаторах, в цепях с распределенными параметрами каждый участок линии обладает индуктивностью, емкостью и активным сопротивлением. Эти параметры распределены вдоль всей линии по определенному закону, чаще всего равномерно.

Цепи с сосредоточенными параметрами обычно имеют малые размеры по сравнению с длиной волны. Напряжение и ток в них распространяются по всей цепи за промежутки времени, во много раз меньшие, чем период колебаний. Поэтому процессы в таких цепях рассматриваются только во времени. А длинные линии имеют длину такого же порядка, что и период колебаний. Вследствие этого в длинных линиях необходимо рассматривать процессы не только во времени, но и в пространстве.

Двухпроводные линии характеризуются первичными и вторичными параметрами.

К первичным параметрам линии относят: индуктивность проводников, емкость между ними, активное сопротивление и проводимость. Они приводятся на единицу длины линии (обычно 1 м) и называются погонными (L1, C1, R1, s1). Погонные параметры зависят от конструкции линии. Чем больше поверхность проводников линии и чем меньше расстояние между ними, тем больше погонная емкость C1 и тем меньше погонная индуктивность L1. Обычно L1 имеет порядок единиц микрогенри на метр, а C1 составляет несколько пикофарад на метр. Например, для коаксиальной линии индуктивность определяется формулой

L₁=0.46 lg(D/d) (1.1)

а емкость – формулой

C₁=2L₁/lg(D/d) (1.2)

где D – диаметр внешнего проводника, а d – диаметр внутреннего провода.

К вторичным параметрам относят скорость распространения электромагнитной энергии по линии v, волновое сопротивление линии r и другие, которые будут рассмотрены ниже.

При анализе процессов в линии ее удобно представлять в виде бесконечно большого числа бесконечно малых отрезков, каждый из которых можно рассматривать как элементарную ячейку, обладающую сосредоточенными параметрами малой величины. В случае идеальной линии в элементарной ячейке содержатся только индуктивность и емкость.

Рассмотрим бесконечную длинную линию, на входе которой включен генератор синусоидальной Э. Д. С. (рис.1.1.)

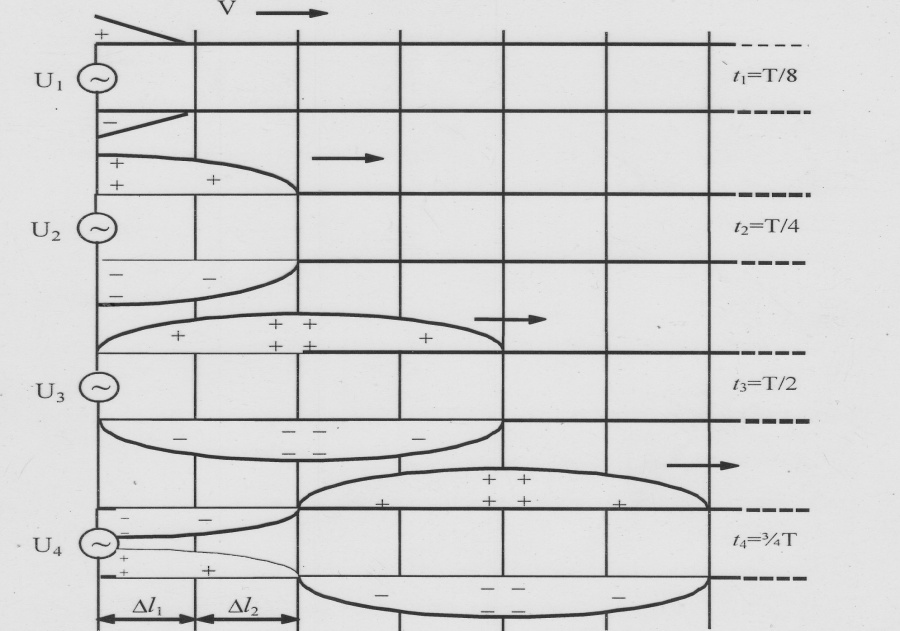
Рис. 1.1. Бегущая волна в линии

Допустим, что генератор включен в момент времени t=0.

Через некоторое время Dt₁ напряжение генератора увеличится от 0 до u₁, до этого же напряжения зарядится распределенная емкость отрезка линии Dl₁. Верхний провод этого отрезка получит некоторый положительный заряд, а нижний провод – отрицательный.

Заряды участка Dl₁ создают на нем электрическое поле, т.е. между проводами линии появится разность потенциалов, под влиянием которой заряды начинают перемещаться на соседний участок Dl₂, на котором зарядов еще нет. Потенциал верхнего провода на участке Dl₂ ниже, чем на участке Dl₁, а потенциал нижнего провода выше. За промежуток времени Dt₂ заряды с участка Dl₁ перемещаются на участок Dl₂, и этот участок заряжается до напряжения u₁. За это же время напряжение генератора увеличивается от u₁ до u₂ и т.д.

Таким образом, под действием Э. Д. С. генератора вдоль каждого участка линии движутся заряды. Процесс распространения зарядов вдоль линии называется бегущей волной зарядов. Бегущие волны зарядов являются бегущими волнами тока и напряжения, поэтому процесс перемещения зарядов вдоль линии называется бегущей волной тока, а процесс распространения напряжения – бегущей волной напряжения.

Каждая синусоида, изображённая на рис.1.1.,отражает распределение напряжения вдоль линии для некоторого момента времени. Для следующего момента кривая смещена вдоль оси, так как волна распространяется от генератора. Можно показать графически изменение напряжения во времени для какой-либо точки линии. Оно также изобразится синусоидой, но вдоль горизонтальной оси будет отложено время. Это будет график колебаний в данной точке линии, а не график бегущей волны.

В бегущей волне изменения тока и напряжения совпадают по фазе. Поэтому кривые рис. 1.1. одновременно изображают распределение и тока, и напряжения.

Если Э. Д. С. генератора непрерывно меняется, то напряжение, которое было на генераторе раньше, успеет к конкретному времени распространиться вдоль линии на большее расстояние, чем напряжение, возникшее позже.

Распределение напряжения вдоль линии условно изображено на рисунке около верхнего провода, который принят за ось абсцисс. Кривые построены для трех последовательных моментов времени t₁, t₂, t₃. Из рисунка следует, что распределение напряжения перемещается во времени вдоль линии. То же происходит и с распределением тока. Таким образом, распределение во времени вдоль линии напряжения и тока получило название бегущей волны. Бегущие волны распространяются вдоль линии со скоростью, близкой к скорости света.

Пусть напряжение генератора, подключенного к линии, изменяется по закону u=U_mcoswt. Между точками, находящимися на расстоянии х, изменения напряжения запаздывают на время Dt=x/v, где v – скорость распространения волны. Поэтому напряжение между симметричными точками проводов

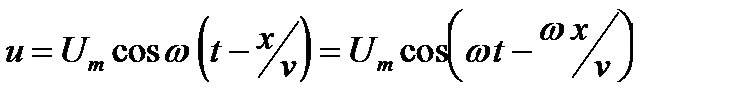(1.3)

С учетом , где 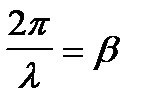– коэффициент фазы.

Это и есть уравнение бегущей волны напряжения. Уравнение бегущей волны тока подобно уравнению бегущей волны напряжения, т.к. ток и напряжение синфазны.

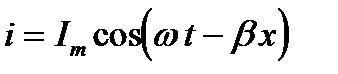,(1.4)

Ток и напряжение являются функциями времени и расстояния. Задаваясь определенным временем t, можно найти распределение напряжения и тока вдоль линии или, выбрав точку на линии, можно определить ток в ней и напряжение в любой момент времени.

Линия передач характеризуется целым рядом вторичных параметров:

· волновое сопротивление r

Сопротивление линии бегущей волне тока называется волновым сопротивлением линии r. Волновое сопротивление линии является активным.

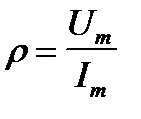, где U_m – амплитуда бегущей волны напряжения, I_m – амплитуда бегущей волны тока.

Волновое сопротивление линии является активным. Но это не означает, что это сопротивление поглощает энергию бегущей волны. В идеальной линии волновое сопротивление образовано реактивными сопротивлениями (индуктивным и емкостным), которые не поглощают энергию. Активный характер волнового сопротивления указывает на равенство в каждый момент времени в любом элементе идеальной линии энергий электрического и магнитного полей, а следовательно, на равенство фаз бегущих волн тока и напряжения. Оно зависит от длины линии. В любом элементе линии в каждый момент времени энергия запасаемая в в распределенных индуктивностях, должна быть равна энергии, запасаемой в распределенных емкостях (в противном случае линия носила бы реактивный характер).

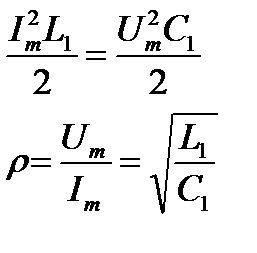
Т.о. волновое сопротивление определяется конструкцией линии. Для наиболее часто встречающихся конструкций значения r приведены в справочной литературе.

· входное сопротивление линии Z_ВХ– отношение амплитуды напряжения к амплитуде тока на входе линии

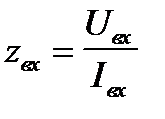
Так как максимальные и действующие значения напряжения и тока бегущих волн не меняются по длине линии и эти волны совпадают по фазе

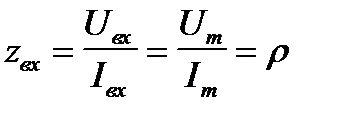
т.е. входное сопротивление, оказываемое бегущей волне, равно волновому сопротивлению линии. Волновое сопротивление можно определить, как входное сопротивление бесконечно длинной линии.

Если бесконечную линию разорвать на конечном от генератора расстоянии и нагрузить на R_н=r, то такая линия называется согласованной и режим бегущих волн в ней не нарушается. При этом энергия генератора будет полностью поглощаться нагрузкой. В случаях, когда линия предназначена для передачи ЭМЭ она должна быть согласованной.

· скорость распространения бегущей волны вдоль линии

Скорость распространения бегущей волны вдоль линии определяется конструктивными особенностями линии и равна

, где L₁ и C₁ – погонные емкость и индуктивность

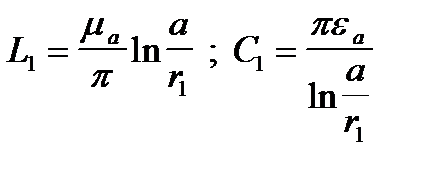, где e_а, m_а – абсолютная магнитная и диэлектрическая проницаемости среды;

а – расстояние между проводами линии;

r₁ – радиус провода линии.

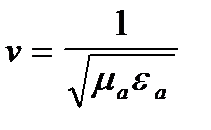, (1.5)

Изменяя емкость, индуктивность линии, либо изменяя свойства диэлектрика можно изменять скорость распространения бегущей волны вдоль линии.

Процесс распространения бегущей волны вдоль длинной линии без потерь характерен следующим:

1. Амплитуда напряжения (тока) одинакова во всех точках линии (т.е. z_вх=r).

2. В любом поперечном сечении линии напряжение и ток изменяются с одинаковой фазой (из-за отсутствия реактивности).

3. Фаза напряжения (тока) периодически меняется вдоль линии.

4. Бегущие волны переносят ЭМЭ.