Электрические цепи несинусоидальных токов
В электротехнике считается, что генерацию и распределение электрической энергии лучше всего осуществлять на синусоидальных токах и напряжениях, передачу — на синусоидальных и постоянных токах и напряжениях, а для управления работой электроустановок применять разрывные функции токов и напряжений (типа «меандр», рис. 1.29, а). При этом в элементах преобразования синусоидальных токов и напряжений в постоянные и разрывные токи и напряжения, появляются токи и напряжения, описываемые кусочно-синусоидальными функциями (рис. 1.29, б).
На практике из-за изменения во времени параметров потребителей электроэнергии, воздействий на электрические цепи со стороны внешней среды, но главным образом, из-за использования в цепях нелинейных элементов реальные токи и напряжения цепей имеют гораздо более сложный вид. В качестве примера на рис. 1.29, в представлен характерный для практики вид искаженного синусоидального напряжения. Для анализа подобных несинусоидальных режимов цепей и оценки их качества необходим специальный математический аппарат, инвариантный к многообразию возможных форм токов и напряжений и удобный для проведения их расчетов. В электротехнике в качестве такого аппарата выбран Фурье-анализ периодических функций. При этом периодические функции 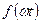 ЭДС, токов, напряжений представляют в виде ряда:
ЭДС, токов, напряжений представляют в виде ряда:
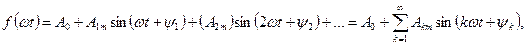
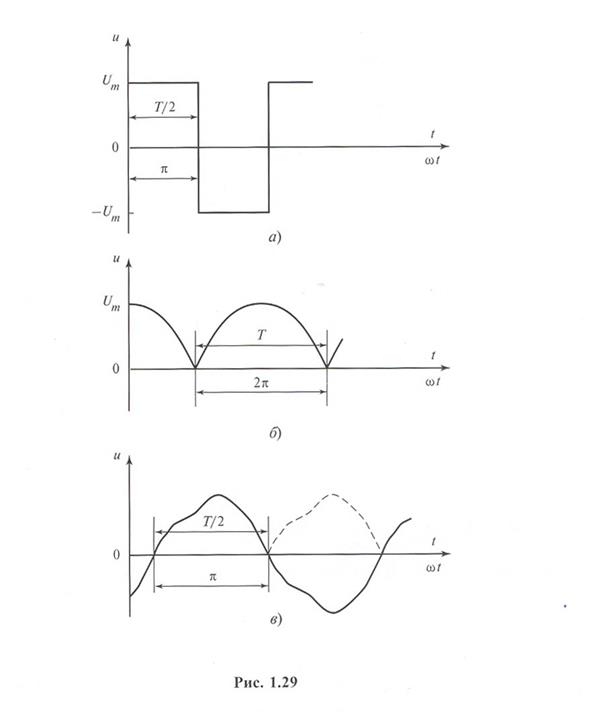
в котором первый член А0 называют постоянной составляющей или нулевой гармоникой функции 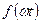 , второй член —
, второй член — 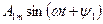 — ее основной или первой гармоникой, а остальные члены ряда
— ее основной или первой гармоникой, а остальные члены ряда 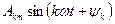 , к > 2— высшими гармониками. Величину
, к > 2— высшими гармониками. Величину 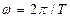 называют основной угловой частотой (Т — период функции
называют основной угловой частотой (Т — период функции 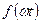 ) Ряд может быть представлен и в иной форме:
) Ряд может быть представлен и в иной форме:
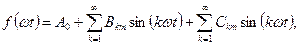
где 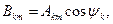
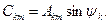 Коэффициенты А0, Bkm, Ckm, Akm, для функции
Коэффициенты А0, Bkm, Ckm, Akm, для функции 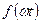 , заданной аналитически, могут быть определены по соответствующим справочникам рядов Фурье или в случае, когда она задана численно, рассчитаны по формулам:
, заданной аналитически, могут быть определены по соответствующим справочникам рядов Фурье или в случае, когда она задана численно, рассчитаны по формулам:
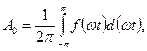
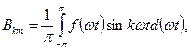
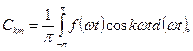
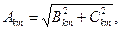
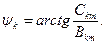
При наличии определенных видов симметрии функции 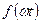 некоторые из коэффициентов ее ряда Фурье обращаются в ноль, а сам ряд имеет более простой вид. Так, если рассматриваемая функция удовлетворяет условию
некоторые из коэффициентов ее ряда Фурье обращаются в ноль, а сам ряд имеет более простой вид. Так, если рассматриваемая функция удовлетворяет условию 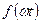 =
= 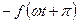 , т.е. ее график, сдвинутый на полпериода (см. пунктир на рис. 1.29, в) будет симметричен относительно оси абсцисс исходному графику, то ее ряд Фурье не будет содержать постоянной составляющей и четных гармоник
, т.е. ее график, сдвинутый на полпериода (см. пунктир на рис. 1.29, в) будет симметричен относительно оси абсцисс исходному графику, то ее ряд Фурье не будет содержать постоянной составляющей и четных гармоник
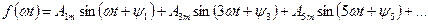
Если функция 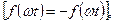 т.е. ее график симметричен относительно оси ординат, то ее ряд не будет содержать синусов
т.е. ее график симметричен относительно оси ординат, то ее ряд не будет содержать синусов
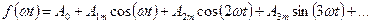
Например, ряд функции 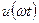 , представленной на рис. 1.29, б имеет вид
, представленной на рис. 1.29, б имеет вид
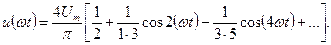
Если же функция 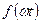 — нечетная,
— нечетная, 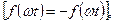 т.е. ее график симметричен относительно начала координат, то ее ряд не будет содержать косинусов и постоянной составляющей
т.е. ее график симметричен относительно начала координат, то ее ряд не будет содержать косинусов и постоянной составляющей
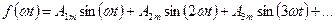
Заметим, что функция 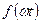 может одновременно удовлетворять сразу двум из перечисленных выше условий. Так, ряд функции
может одновременно удовлетворять сразу двум из перечисленных выше условий. Так, ряд функции 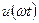 , изображенной на рис. 1.29, а, удовлетворяющей условиям
, изображенной на рис. 1.29, а, удовлетворяющей условиям 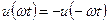 и
и 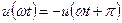 , не содержит косинусов, постоянной составляющей и четных гармоник:
, не содержит косинусов, постоянной составляющей и четных гармоник:
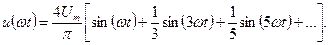
Заметим, что изображенная на рис. 1.29, а функция 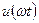 (меандр) разрывная, в то время как все члены ее ряда Фурье функции непрерывные, Для подобных функций имеет место явление Гиббса, когда в окрестностях точек разрыва ряд Фурье (правая часть последнего выражения) будет
(меандр) разрывная, в то время как все члены ее ряда Фурье функции непрерывные, Для подобных функций имеет место явление Гиббса, когда в окрестностях точек разрыва ряд Фурье (правая часть последнего выражения) будет
численно несколько отличаться от исходной функции (левой части последнего выражения).
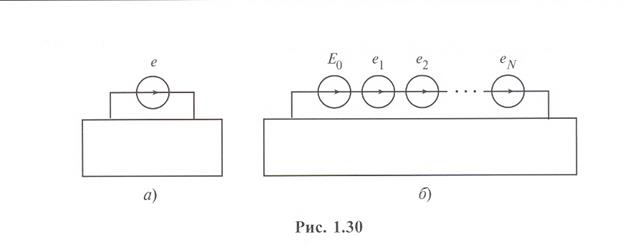
На практике для расчета несинусоидальных режимов используют не бесконечные, а усеченные ряды Фурье, ограничиваясь первыми их (N +1)-членами. При этом некоторую ЭДС (рис. 1.30, а) можно представить в виде последовательно соединенных (N + 1) ЭДС (рис. 1.30, б):
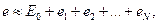
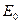 — постоянная, а еj= 1,2, ...,N, — гармонические составляющие е =
— постоянная, а еj= 1,2, ...,N, — гармонические составляющие е = 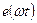
При этом Фурье-анализ несинусоидальных режимов цепей может быть сведен к выполнению трех этапов:
1. Функции всех ЭДС (источников тока) цепи заменяют усеченными рядами Фурье, а сами источники ЭДС (тока) — последовательно (параллельно) соединенными источниками постоянной (постоянного) и ряда гармонических ЭДС (источников тока).
2. Цепь рассчитывается отдельно по постоянной и каждой гармонической составляющей тока.
3. Результаты расчета суммируются согласно принципу наложения.
При выполнении второго этапа анализа можно гармонические составляющие токов и напряжений цепи рассчитывать с использованием комплексного (символического) метода. В этом случае следует учитывать различие значений индуктивных и емкостных сопротивлений на разных гармониках (см. табл. 1.1).
Пример 1.7.Рассчитаем ток 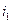 , в схеме рис. 1.10 с ЭДС
, в схеме рис. 1.10 с ЭДС 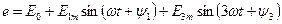 , для чего заменим схему рис. 1.10
, для чего заменим схему рис. 1.10
| Таблица 1.1 | ||
| Элемент | Комплексное сопротивление на основной гармонике | Комплексное сопротивление на высших гармониках |
| Катушка | 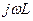
| 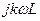
|
| Конденсатор | 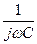
| 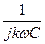
|
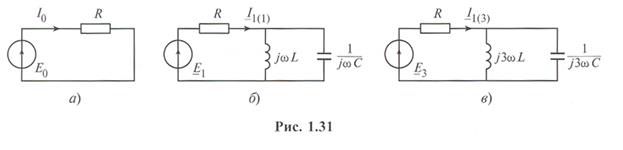
тремя схемами (рис. 1.31, а —в), соответствующими нулевой, первой и третьей гармоникам ЭДС.
Расчет схемы рис. 1.31, а дает I0= E0/R, схемы 1.31, б -
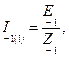
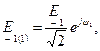
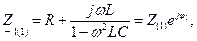
схемы 1.31, в —
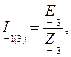
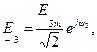
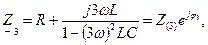
где 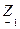 и
и 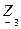 — входные комплексные сопротивления цепи на первой и третьей гармонике. Окончательно, согласно принципу наложения, имеем
— входные комплексные сопротивления цепи на первой и третьей гармонике. Окончательно, согласно принципу наложения, имеем
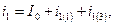
где 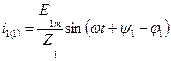 ,
, 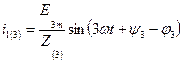
В заключение отметим, что несинусоидальные периодические токи, напряжения, ЭДС также как и синусоидальные могут быть интегрально охарактеризованы действующими значениями. Под действующими значениями несинусоидальных токов, напряжений, ЭДС понимаются их среднеквадратичные значения за период
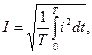
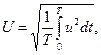
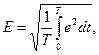
Можно показать, что действующее значение периодического несинусоидального тока, напряжения, ЭДС равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник
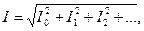
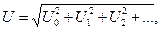
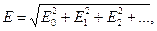
Дата добавления: 2014-12-21; просмотров: 1826;
