Упругость
Под упругостью тела понимают его способность изменять форму и размеры под действием силы и восстанавливать их после снятия силы.
Упругое тело подчиняется закону Гука: деформация пропорцианальна действующей силе. При простом (одноосном) растяжении или сжатии (рис. 1) выражение закона Гука имеет вид:
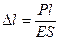 ,
,
где
Р – действующая сила;
l – длина базы измерения на образце до приложения силы;
Е – коэффициент пропорциональности (модуль упругости образца 1 рода);
S – площадь поперечного сечения образца до приложения нагрузки.
В соответствие с рис. 1:
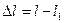 – абсолютная продольная деформация образца;
– абсолютная продольная деформация образца;
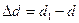 – абсолютная поперечная деформация образца.
– абсолютная поперечная деформация образца.
Отношение 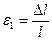 называется относительной продольной деформацией образца.
называется относительной продольной деформацией образца.
Отношение 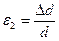 называется относительной поперечной деформацией образца.
называется относительной поперечной деформацией образца.
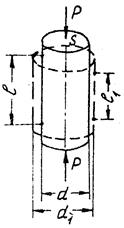
Рис. 1. Упругое сжатие
Отношение 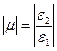 называется коэффициентом поперечной деформации образца (коэффициент Пуассона).
называется коэффициентом поперечной деформации образца (коэффициент Пуассона).
Приведенную выше формулу можно представить в виде:
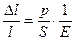 или
или 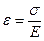 .
.
Откуда 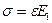 ,
,
где 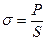 – нормальное напряжение.
– нормальное напряжение.
Графическая зависимость между σ и ε носит название «напряжение – деформация» (рис. 2–5).
По виду диаграммы «напряжение – деформация» тела разделяются на абсолютно упругие, вполне упругие, упругие и неупругие.
Для абсолютно упругого тела (рис. 2):
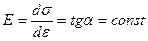 .
.
Для вполне упругого тела (рис. 3):
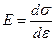 ;
; 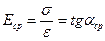 .
.
Для упругого тела (рис. 4) модули упругости при нагружении Ен и разгрузки Ер различны. Работа нагружения Ан больше работы разгрузки Ар на величину рассеянной энергии L:
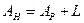 .
.
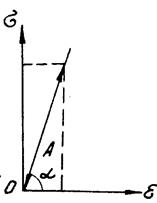
Рис. 2. Абсолютное упругое тело
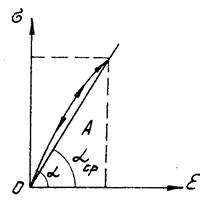
Рис. 3. Вполне упругое тело
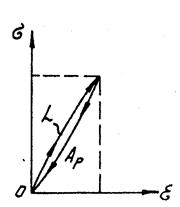
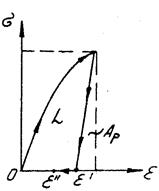
Рис. 4. Упругое тело Рис. 5. Неупругое ело
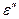 – остаточная деформация;
– остаточная деформация;
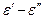 – упругое последействие
– упругое последействие
Работа упругой деформации обратима для абсолютно и вполне упругих тел
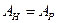
Для упругих (рис. 4) и неупругих (рис. 5) тел работа деформации необратима
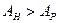
Физико-механические свойства горных пород меняются с изменением величины напряжения. При малых напряжениях большинство из них проявляет упругие свойства.
Дата добавления: 2014-12-21; просмотров: 862;
