Индексы

главное назначение – обеспечить эффективный прямой доступ к кортежу по ключу. Обычно определяется для одного отношения и строится по значению какого-либо атрибута. Если этот атрибут является ключом отношения, то индекс должен быть уникальным, т.е. не содержать дублированных значений ключа.

Помимо таких индексов рассматриваются индексы, связанные с несколькими отношениями (мультииндексы). В них ключ индекса является составным, по отдельным составляющим его составляются кортежи из разных отношений. Такие мультииндексы используются для сложных операций (эквисоединение).

Общая идея организации – хранение упорядоченного списка ключей с привязкой к каждому ключу идентификатора кортежа или списка идентификаторов кортежа, если ключи индекса не уникальны.

Отношение А индекс отношения А по ключу Атр.1

Атр.1 | | ключ | tid |

a | | a | 1 | ключ | tid

b | | Þ a | 4 | или a | 1, 4 – список tid

c | | b | 2 | b | 2

a | | c | 3 | c | 3

Отношение B индекс отношения B по ключу Атр.2

Атр.2 | | ключ | tid |

10 | | 2 | 2 |

2 | | Þ 8 | 4 |

14 | | 10 | 1 |

8 | | 14 | 3 |

мультииндекс отношений А и В по ключам Атр.1 и Атр.2:

| a 2 | 1, 2 || a 14

| a 2 | 4, 2 || a 14

| a 8 | ... || b 2

| a 8 | || b 8

| a 2 | || ...

| a 2 | ||

Большинство СУБД строит индекс сразу, как только определит ключ. Существует много способов построения индексов, но самым распространённым является способ ”B(b)-деревьев”.

B-дерево обладает двумя свойствами:

1) сбалансированность – длина пути от корня до любого места одна и та же;

2) ветвистость – это свойство каждого узла ссылаться на большое количество потомков.

Каждый узел B-дерева соответствует страница ВП. Внутренние страницы и листовые страницы должны иметь разную структуру:

I. внутренняя.

№1(ключ 1), №2(ключ 2), …, №m(ключ m): здесь содержатся номера страниц и ключи.

Ключ каждой страницы удовлетворяет условиям:

– кл.1 <= кл.2 <= … <= кл.m (<= – предшествует или равен);

– на странице №S находятся ключи: кл.S <= k <= кл.(S+1).

II. листовая.

Кл.1 <= кл.2 <= …

А списки – списки идентификаторов кортежей, которые имеют отношение к данному ключу. Элементы в списке могут быть однонаправленными или двунаправленными:

Поиск в B-дереве – это прохождение от корня к листу в соответствии с данным значением ключа. Т.к. дерево сильно ветвистое, таких переходов не будет слишком много, а т.к. оно сбалансировано, поиск происходит всегда за одинаковое количество шагов.

	Ссылки на соответствующие кортежи		Ключ2 – неуспешный поиск Ключ1,3 – успешный

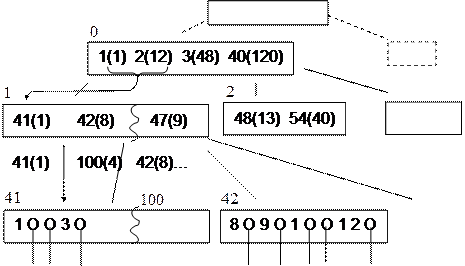Скорость операции сравнения: (поиск) log_mn,

Где n – число ключей, m – степень ветвистости.

Основная проблема – поддержание свойств B-дерева при добавлении и исключений записей.

Рассмотрим алгоритм добавления новой записи:

1) поиск по ключу: если B-дерево не содержит записей с таким ключом, то будет получен № страницы, где этот ключ должен содержаться;

2) вставка: нужно вытащить эту страницу в буфер ОЗУ и там модифицировать листовую страницу:

– если размер достаточен, то вытолкнуть после модификации во ВП;

– если информации на странице больше, чем её размер (переполнение буфера), необходимо её расщепить. Т.е. эта страница делится на две, каждая из которых меньше объёма буфера, но на новую страницу необходимо добавить ссылку, а, следовательно, на предыдущей уровень нужно внести изменения в список ключей. Если эта страниц тоже переполнилась, то её опять нужно расщепить и т.д. Если вдруг переполнится корневая страница, то придётся её расщепить, а создать новый корень над ними.

При удалении записей алгоритм обладает теми же особенностями:

поиск: если запись не найдена, то и удалять нечего, иначе физическое удаление соответствующего ключа и после этого проверка: если информации на странице очень мало, то можно осуществить слияние этой страницы с “левым” или ”правым” соседом и после этого откорректировать список предыдущего уровня.

Для большей эффективности используется упреждающее расщепление не при переполнении, а по достижении заполненности страницы некоторого уровня.

В литературе такие деревья называют B+, B*. Альтернативой B-деревьев является хеширование информации.