Дислокации. Дислокации в кристаллах – специфические линейные дефекты, нарушающие правильное чередование атомных плоскостей

Дислокации в кристаллах – специфические линейные дефекты, нарушающие правильное чередование атомных плоскостей. В отличие от точечных дефек­тов, нарушающих ближний порядок, дислокации нарушают дальний порядок в кристалле, искажая всю его структуру.

Кристалл с правильной решеткой можно изобразить в виде семейства параллельных атомных плоскостей (рис. 2,а)

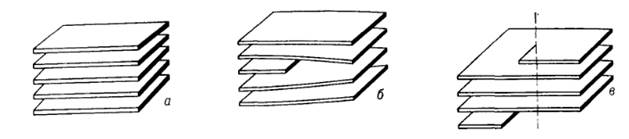
Рис. 14.2. Основные виды дислокаций

Идеальная система атомных плоскостей (а);

краевая дислокация (б); винтовая дислокация (в)

Если одна из плоскостей обрывается внутри кристалла (рис. 2,б), то ее край образует линейный дефект, называемый краевой дисло­кацией. Рис. 2,в иллюстрирует другой простейший тип дислокации – винтовую дислокацию. Здесь ни одна из атомных плоскостей не оканчивается внутри кристалла, но сами плоскости лишь приблизительно параллельны и смыкаются друг с другом так, что фактически кристалл состоит из единствен­ной винтообразно изогнутой атомной плоскости.

При каждом обходе вокруг оси дислокации эта «плоскость» поднимается (или опускается) на один шаг винта, равный межплоскостному расстоянию. Ось винтовой лестницы и обра­зует линию дислокации.

Основной геометрической характеристикой дислокации является так называемый вектор Бюргерса. Для отыскания век­тора Бюргерса нужно составить из векторов трансляции контур так, чтобы он замыкался в идеальной решетке. Тогда этот контур (контур Бюргерса), построенный вокруг линии дислокации, окажется разорванным (рис. 3). Вектор трансляции, который нужно провести для того, чтобы соединить на­чало и конец контура, и называется вектором Бюргерса дислокации.

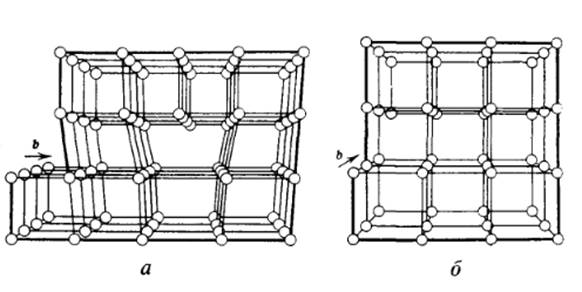
Рис. 14.3. Вектор Бюргерса для краевой дислокации (а)

и для винтовой дислокации (б)

В случае краевой дислокации (рис.14.3,а) вектор Бюргерса перпендикулярен линии дислокации, а его длина равна лишнему межплоскостному расстоянию, соответствующему оборванной пло­ским. В случае винтовой дислокации (рис. 14.3,б) вектор Бюргерса парал­лелен дислокации и равен но величине шагу винта. При других значениях угла между дислокацией и вектором Бюргерса получаются смешанные дислокации.

Ширина области дислокации не превышает нескольких междуатомных расстояний. Вдали от этой области ис­кажения решетки столь малы, что ими обычно пренебрегают.

Для краевой дислокации принимается положительный знак, если лишняя полуплоскость находится сверху. Изображенную на рис. 14.3,а краевую дислокацию следует считать положительной.

В положительной дислокации в верхней части кристалла дей­ствуют сжимающие напряжения со стороны неискаженной части кристаллической решетки, а в нижней – растягивающие напряжения. Отрицатель­ная дислокация соответ­ствует случаю, когда часть кристалла выше дислокации подвержена напряжениям растяжения, а нижняя часть – напряжениям сжатия.

Для винтовой дислокации знак зависит от направления обхода контура Бюргерса. Обычно обход производится по часовой стрелке (сети смотреть вдоль условного направлении дислокации), так что на рис 14.3,б винтовую дислокацию следует считать идущей на нас.

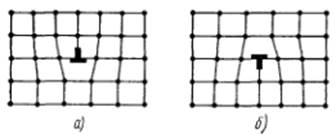Рис. 14.4. Знак краевой дислокации: (а) – положительный; (б) – отрицательный

На рис. 14.4 показаны положительная и отрицательная дислокации, а также значки, которыми они обычно изображаются. Нетруд­но видеть, что эти две дислокации раз­личаются лишь поворотом на 180°. По­этому не имеет смысла говорить о зна­ке дислокации, если эта дислокация

одна: ее знак имеет значение, если рядом есть другая дислокация.

Дислокации взаимодействуют между собой посредством упругих сил: дислокации од­ного знака отталкиваются, дислокации разных знаков притягиваются.

На рис. 14.5 показан кристалл, на ко­торый действует сдвигающее напря­жение, приводящее к пластической деформации. Видно, что граница сдвига АВ, отделяю­щая сдвинутую область от несдвину­той, и есть линия краевой дислокации, перпендикулярная вектору сдвига.

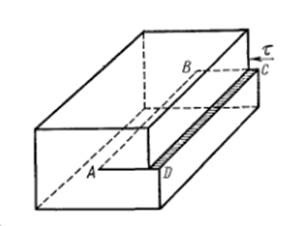Рис. 14.5. Сдвиг, создающий краевую дислокацию

В кристалле началась пласти­ческая деформация: верхняя половина кристалла сдвигается относительно нижней половины по плоскости скольжения. Под действием внешнего механического напряже­ния дислокации в кристалле могут дви­гаться. Поскольку знаки напряжений, создаваемых положительной и отрица­тельной дислокациями, противополож­ны, то

разноименные дислокации движут­ся в разные стороны под действием одного и того же внешнего напряже­ния. Дислокации с разными знаками, движущиеся в одной плоскости, при встрече взаимно унич­тожаются (аннигилируют), в резуль­тате чего восстанавливается целост­ность решетки.

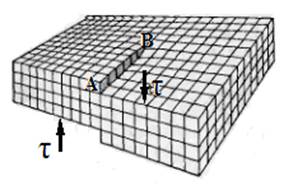Рис. 14.6. Сдвиг, создающий винтовую дислокацию

Винтовая дислокация в кристалле тоже возникает при сдвиге одной части кристалла относительно другой, но, в отличие от краевой дислокации, линия винтовой дислокации параллельна век­тору сдвига (рис. 14.6). Можно представить, что в кристалле произве­ден разрез (рис. 14.7,а), а затем сдвиг вдоль плоскости разреза (рис. 14.7,б). Линия ВС, отделяющая сдвинутую часть от несдвинутой, и есть линия винтовой дислокации. Выход винтовой дислокации на поверхность кристалла заканчивается ступень­кой. Если попробовать «залечить» вин­товую дислокацию,

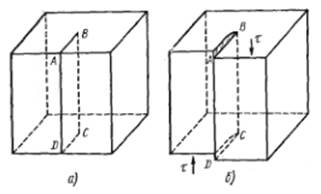Рис. 7. Образование винтовой дислокации

добавив недостаю­щую атомную плоскость, то ступенька только сдвинется на одно межплоско­стное расстояние, но не исчезнет.

Так же, как и для краевой дислока­ции, в случае винтовой дислокации искажения решетки сосредоточены вблизи линии дислокации в узкой об­ласти размером в несколько межатомных расстояний.

Линия дислокации не может кон­чаться внутри кристалла. Она должна либо выходить на поверхность кри­сталла, либо разветвляться на другие дислокации, либо образовывать внут­ри кристалла замкнутую петлю.

Таким образом, дислокация – это граница области незавершенного сдвига внутри кристалла, или нарушение правильности структуры вдоль некоторой линии, которая не может оборваться внутри кристалла. Оба эти определения эквивалентны.

Характерной особенностью дислока­ций является их подвижность: под действием внешних сил дислокация может перемешаться по кристаллу. Это движение дислокации связано с пластической деформацией кри­сталла.

Пусть под действием внешней силы в кристалле произошел сдвиг и гра­ницей области сдвига является крае­вая дислокация (рис. 14.8,а).

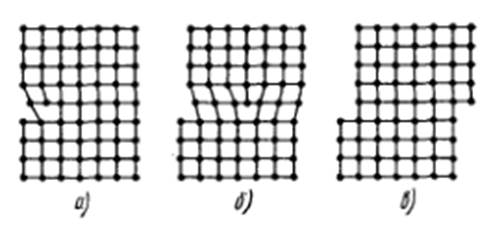
Рис. 14.8. Скольжение краевой дислокации

Для то­го чтобы этот сдвиг распространялся дальше и дислокация передвинулась в плоскости скольжения на одно меж­плоскостное расстояние, не нужен пе­ренос массы и не нужно разрывать связи во всех атомных плоскостях, пе­ресекающих плоскость скольжения. Достаточно, чтобы разорвалась связь по одной соседней плоскости, тогда дислокация переместится на одно межатомное расстояние вправо (рис. 14.8,б). При этом лишняя атом­ная полуплоскость сама никуда не пе­ремещается, а как бы передает «эста­фету» соседней плоскости: целост­ность плоскости, которая была обор­ванной, восстанавливается, а соседняя плоскость становится оборванной.

Сдвиг происходит не одновременно по всей плоскости скольжения, а за­рождается в слабом месте и постепен­но распространяется по плоскости, так что в каждый момент в энергети­чески невыгодном положении находит­ся лишь относительно небольшое ко­личество атомов окаю границы меж­ду сдвинутой и несдвинутой частями кристалла. Граница зоны сдвига, т. е. линия дислокации, перемещается в плоскости скольжения «по эстафете».

Когда скользящая краевая дислока­ция пересекает весь кристалл и вы­ходит на его поверхность, верхняя по­ловина кристалла оказывается сдви­нутой относительно нижней на одно межплоскостное расстояние, так что на боковой поверхности кристалла образуется ступенька, а па всем пути, где прошла дислокация, восстанавли­вается целостность решетки (рис. 14.8,в).

Важно отметить, что скольже­ние дислокации и пластическая де­формация кристалла произошли без переноса массы. Плоскость, в которой движется дислокация, называется плоскостью скольжения.

Кроме движения скольжения, при котором полуплоскость перемещается параллельно самой себе, возможен и другой вид дислокационного движения – когда плоскость движется вдоль самой себя, глубже входя в кристалл или, наоборот, выходя из него. Этот вид движения краевой дислокации называется переползанием.

Количественной характеристикой концентрации дислокаций является параметр, называемый "плотностью дислокаций". Это число линий дислокаций, пересекающих единичную площадку в кристалле, ориентированную под определенным углом к осям координат

Очевидно, что плотность дислокаций может быть разной при различной ориентации этой площадки в кристалле, поэтому плотность дислокаций является, строго говоря, тензорной величиной. Но обычно плотность дислокаций принимают примерно одинаковой для всех направлений, и можно считать, что плотность дислокаций равна числу дислокационных линий, пересекающих единицу площади кристалла в каком-нибудь удобном для наблюдения направлении.

В кристаллах, выращенных обычными методами кристал­лизации из расплава, плотность дисло­каций примерно составляет (10⁴ – 10⁶) см ^-2. Путем специальной термической обработки можно понизить эту плотность до (10³ – 10⁴) см ^-2.

Наилучшие полупроводни­ковые кристаллы, полученные путем выращивания, имеют плотность дисло­кации (10² – 10³) см ^-2. Специально выращенные нитевидные бездислокационные кристаллы (так наз. "усы") содержат всего одну дислокацию и обладают прочностью, существенно превосходящей обычные кристаллы или поликристаллические материалы.

В результате пласти­ческой деформации плотность дисло­каций быстро возрастает на несколько порядков (10⁸ – 10¹⁰) см ^-2.

Чтобы лучше представить это число, отметим, что при плотности дислокаций 10⁸ см ^-2 общая длина всех дислокаций, содержащихся в 1 куб мм кристалла, составляет 1 километр.

Большинство методов эксперимен­тального наблюдения дислокаций ос­новано на регистрации напряжений или искажений в решетке, обуслов­ленных дислокацией.

Рис. 14.9. Фигуры травления на поверхности кристалла сурьмы. Увеличение 600 Х

Одним из простых методов наблюдения дислокаций является метод избирательного травления, т.е. обработ­ка поверхности кристалла специально подобранным химическим реактивом, в результате действия которого на по­верхности образуются мелкие ямки, называемые фигурами травления. Фигуры травления образуются в тех местах, где на поверхность кристалла выходит дислокация и, следовательно, струк­тура кристалла нарушена. Огранка фигуры травле­ния зависит от симметрии грани кри­сталла. Располо­жение и число фигур травления харак­теризуют дислокационную структуру кристалла (рис. 14.9). По числу ямок травления на

площади 1 см² рассчитывается средняя плотность дислокаций в объеме кристалла.

Часто производят послойное травление поверхности, снимая слой за слоем и регистрируя изменение плотности дислокаций по глубине кристалла.

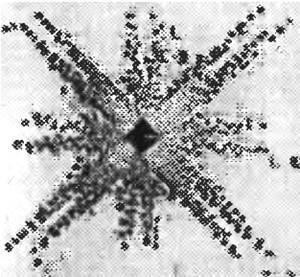Рис. 14.10. Звезда фигур травления на грани (001) кристалла LiF. Увеличение 300Х

Определение плотности дислокаций по фигурам травления является ос­новным промышленным методом контроля качества кристалла, но этот метод применим лишь для кристаллов с плотностью дислокаций, меньшей, чем (106 – 107) см -2. При большей плотности дислокаций уже не удается различить отдельные фигуры травле­ния, они все сливаются друг с другом. Более нагляден, но и более сложен по технике проведения ме­тод декорирования, в котором

дисло­кации делаются видимыми, потому что на них осаждаются чужеродные частицы.

Так, если кри­сталл кремния подвергнуть отжигу в парах золота, то частицы золота осаждаются вдоль дислокационных стенок, делая их видимыми. В отли­чие от метода травления метод деко­рирования позволяет наблюдать ди­слокационную структуру не только на поверхности, но и в глубине кристал­ла.

Собственные поля напряжений дисло­кации, складываясь, создают замет­ные концентрации напряжений внутри кристалла, которые можно наблюдать благодаря пьезооптическому эффекту (фотоупругости). Этот метод особен­но удобен для исследования дислока­ций в кубических кристаллах, которые в ненапряженном состоянии оптиче­ски изотропны. Поля напряжений ди­слокаций в них регистрируются по возникающему двойному лучепрелом­лению.

На рис. 14.11 показано распре­деление дислокаций в кристалличе­ской пластинке кремния, регистрируемое по двойному лучепре­ломлению (а), по методу травления (б) и методом де­корирования (в). На рис. 14.11 (г) показано усредненное по всем трем методам распределение дислокаций. Видно, что во всех случаях картины распределения дислокаций в основном совпадают.

Рис. 14.11. Дислокационная структура пластинки кремния, выявленная различными методами:

а) по двойному лучепре­ломлению,

б) по методу травления,

в) методом де­корирования

г) схема расположения дислокаций

Очень широко распространен метод наблюдения дислокаций с помощью электронного микроскопа. Метод основан на эффекте дислокационного контра­ста, возникающего из-за взаимодей­ствия электронного пучка со смещен­ными атомами в поле напряжений вокруг дислокации. Вследствие интерференции между проходящим и дифрагированным электронными пуч­ками в электронном микроскопе уда­ется увидеть изображение линий ди­слокаций, дефектов упаковки, дисло­кационных рядов и стенок.

Возможности этого метода ограни­чены шириной пучка, позволяющей исследовать лишь небольшой участок кристалла, и, главное, тем, что мож­но исследовать материалы лишь в виде тонких пленок толщиной не больше 100—500 нм. Для получения такой пленки материал прокатывает­ся до тонкой фольги или утоньшается другими методами: резкой, механиче­ской или химической полировкой. Од­нако при всех этих обработках в пленку вносятся новые дефекты, по­этому дислокационная структура пленки не соответствует структуре массивного образца, т. е. по получае­мой картине нельзя однозначно су­дить о структуре исходного кристал­ла.

Рис. 14.12. Ряды атомов и краевая дислокация в кристалле CuS