Свойства определенного интеграла
1) 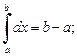
2) 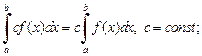
3) 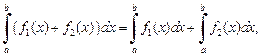
равенства 2 и 3 в совокупности называются свойством линейности;
4) 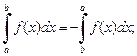
5) 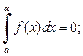
6) значение интеграла не зависит от обозначения переменной интегрирования:
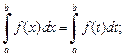
7) свойство аддитивности: при любом взаимном расположении чисел a, b, c имеет место формула:
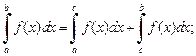
8) если 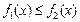 при
при 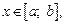 то
то 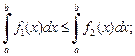
9) если m и M – соответственно наименьшее и наибольшее значения функции 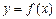 на отрезке [a; b], то верна оценка
на отрезке [a; b], то верна оценка
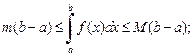
10) 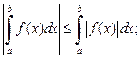
11) если функция f (x) непрерывна на отрезке [a; b], то существует точка 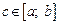 такая, что
такая, что
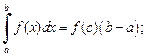
12) если f (x) – нечетная функция, то
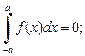
13) если f (x) – четная функция, то
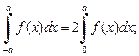
14) если f (x) – периодическая функция периода T, то при любом 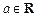 верно равенство
верно равенство
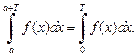
Предполагается, что все интегралы, приведенные в свойствах 1–14, существуют.
Пример 1. Вычислить по определению интеграл 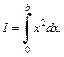
Решение. Функция 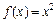 интегрируема на отрезке [0; b], поскольку она непрерывна. Разобьем отрезок [0; b] на n частей точками
интегрируема на отрезке [0; b], поскольку она непрерывна. Разобьем отрезок [0; b] на n частей точками 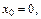
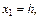
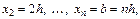 где
где 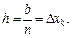
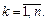
В качестве точек 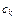 возьмем крайние правые точки каждого частичного отрезка
возьмем крайние правые точки каждого частичного отрезка 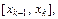 т. е.
т. е.
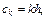
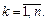
Вычислим значения функции 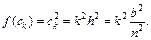
Составим интегральную сумму
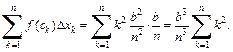
Методом математической индукции можно доказать, что
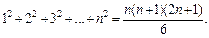
Тогда получаем:
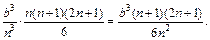
Имеем:
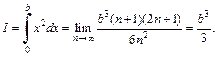
Пример 2. Доказать, что функция Дирихле
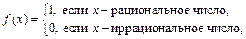
не интегрируема на отрезке [0; 1].
Решение. Разобьем отрезок [0; 1] произвольным образом на n частичных отрезков. При составлении интегральной суммы выберем в качестве точек 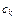 рациональные числа. Тогда
рациональные числа. Тогда 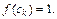
Получаем:
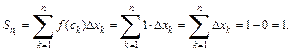
Затем составим интегральную сумму, выбрав в качестве точек 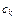 иррациональны числа. Тогда
иррациональны числа. Тогда 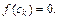 Получаем:
Получаем:
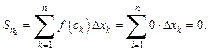
Таким образом, интегральные суммы могут принимать как значение, равное 1, так и значение, равное 0. Следовательно, предел интегральных сумм не существует, т. е. функция Дирихле не интегрируема на отрезке [0; 1], хотя и ограничена на всей числовой прямой.
Пример 3. Сравнить интегралы 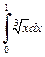 и
и 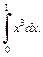
Решение. Так как 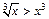 при
при 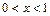 (рис. 20.2), то по свойству сравнения определенных интегралов (см. 8-е свойство) имеем:
(рис. 20.2), то по свойству сравнения определенных интегралов (см. 8-е свойство) имеем:

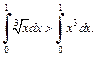
Рис. 20.2
Пример 4. Доказать неравенство 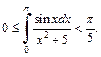
Решение. Так как 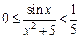 при
при 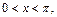 то по 9-му свойству определенных интегралов имеем:
то по 9-му свойству определенных интегралов имеем:
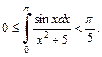
Пример 5. Оценить интеграл 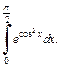
Решение. Так как 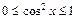 при
при 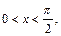 то
то 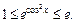 Тогда по 8-му свойству определенных интегралов получаем:
Тогда по 8-му свойству определенных интегралов получаем:
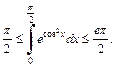
Пример 6. Вычислить определенный интеграл:
1) 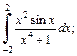 2)
2) 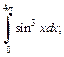 3)
3) 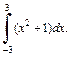
Решение. 1) Так как подынтегральная функция 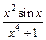 является нечетной, а отрезок интегрирования симметричен относительно начала координат, то
является нечетной, а отрезок интегрирования симметричен относительно начала координат, то 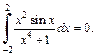
2) Функция 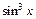 является периодической с периодом
является периодической с периодом 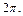 Используем 7-е и 14-е свойства интеграла:
Используем 7-е и 14-е свойства интеграла:
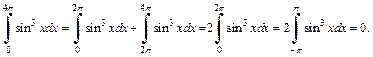
Последний интеграл равен нулю в силу нечетности функции 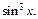
3) Функция 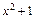 является четной, а отрезок интегрирования симметричен относительно начала координат, поэтому
является четной, а отрезок интегрирования симметричен относительно начала координат, поэтому
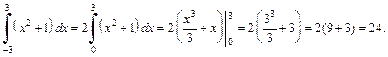
Дата добавления: 2015-09-29; просмотров: 1060;
