Интегралы от дифференциальных биномов
Дифференциальным биномом называется выражение вида
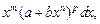 (19.32)
(19.32)
где m, n, p – рациональные числа; a, b – действительные числа, отличные от нуля.
Если 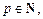 то можно использовать формулу бинома Ньютона, и этим сводим интеграл к интегралу от степенной функции. В общем случае интегралы от дифференциальных биномов, т. е.
то можно использовать формулу бинома Ньютона, и этим сводим интеграл к интегралу от степенной функции. В общем случае интегралы от дифференциальных биномов, т. е. 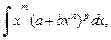 можно привести к интегралу от рациональной функции в следующих трех случаях:
можно привести к интегралу от рациональной функции в следующих трех случаях:
1) если p – целое число, 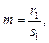
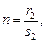
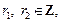
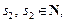 то применяется подстановка
то применяется подстановка 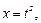 где
где 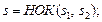
2) если 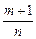 – целое число,
– целое число, 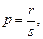
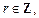
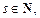 то применяется подстановка
то применяется подстановка 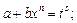
3) если 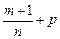 – целое число,
– целое число, 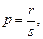
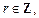
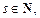 то применяется подстановка
то применяется подстановка 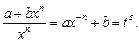
Пример 1. Найти неопределенный интеграл:
1) 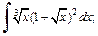 2)
2) 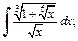
3) 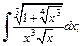 4)
4) 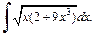
Решение. 1) Запишем подынтегральную функцию в виде дифференциального бинома (19.32)
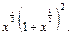
Тогда 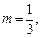
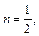
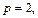 т. е. p – целое число. Следовательно, имеем первый случай интегрируемости дифференциального бинома. Так как
т. е. p – целое число. Следовательно, имеем первый случай интегрируемости дифференциального бинома. Так как 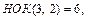 то применим подстановку
то применим подстановку 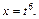 Тогда
Тогда 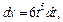
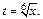
Вычисляем:
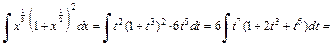
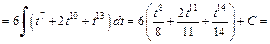
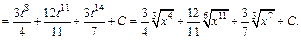
2) Запишем подынтегральную функцию в виде дифференциального бинома (19.32)
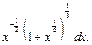
Тогда 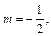
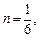
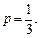
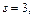
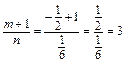 – целое число.
– целое число.
Следовательно, здесь мы имеем второй случай интегрируемости дифференциального бинома. Используем подстановку 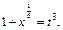
Тогда 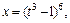
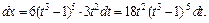
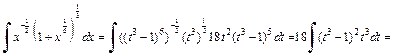
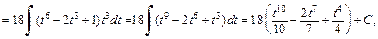
где 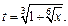
Получаем ответ:
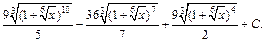
3) Запишем подынтегральную функцию в виде (19.32)
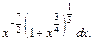
Тогда 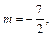
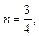
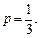
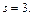
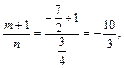
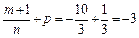 – целое число. Следовательно, имеем третий случай интегрируемости дифференциального бинома. Используем подстановку
– целое число. Следовательно, имеем третий случай интегрируемости дифференциального бинома. Используем подстановку 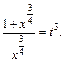
Тогда 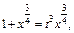
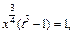
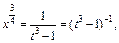
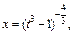
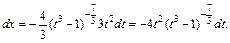
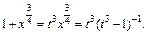
Переходя в подынтегральном выражении к переменной t, получаем:
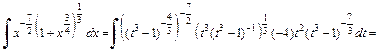
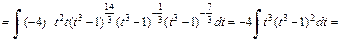
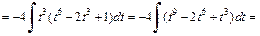
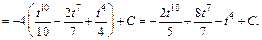
Заменяем t на 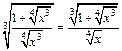 и получаем ответ:
и получаем ответ:

4) Запишем подынтегральную функцию в виде дифференциального бинома (19.32)
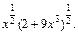
Тогда 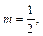
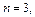
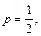
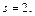
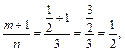
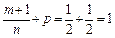 – целое число. Следовательно, имеем третий случай интегрируемости дифференциального бинома. Используем подстановку:
– целое число. Следовательно, имеем третий случай интегрируемости дифференциального бинома. Используем подстановку: 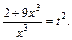 Тогда
Тогда
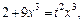
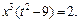
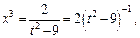
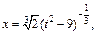
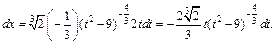
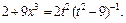
Интеграл преобразуется к виду
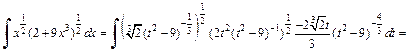
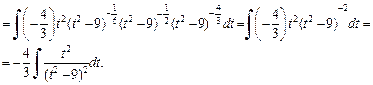
Последний интеграл можно вычислить двумя способами: либо разложить подынтегральную рациональную дробь на сумму простейших дробей либо применить формулу интегрирования по частям.
Вычислим 2-м способом.
Положим 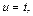
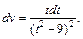
Тогда
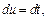
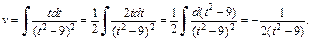
Получим:
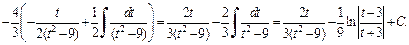
Заменяем t на 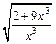 и окончательно получаем:
и окончательно получаем:
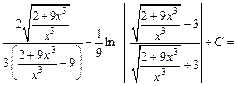
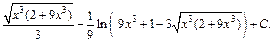
Пример 2. Найти интеграл 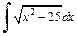 разными способами.
разными способами.
Решение. 1-й способ. Для вычисления интеграла используем формулу интегрирования по частям. Положим 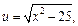
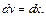 Тогда
Тогда 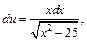
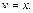
Имеем:
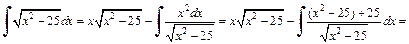
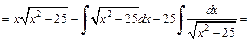
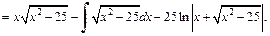
В правой части этого равенства получили исходный интеграл. Найдем его из уравнения
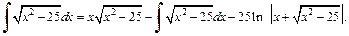
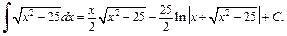
2-й способ. Для вычисления интеграла применим тригонометрическую подстановку 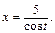
Тогда 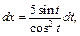
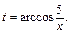
Интеграл примет вид:
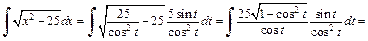
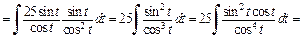
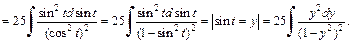
Подынтегральная функция является правильной рациональной дробью. Разложим ее на сумму простейших дробей:
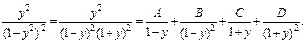
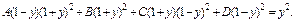 (19.33)
(19.33)
Полагая 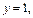 получаем
получаем 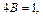
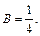
Полагая 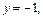 получаем
получаем 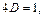
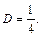
Находим производную от обеих частей равенства (19.33):
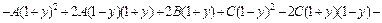
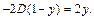
Полагая 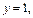 получим
получим 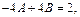
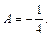
Полагая 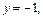 получим
получим 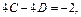
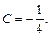
Тогда разложение данной дроби на простейшие имеет вид:
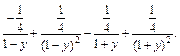
Приходим к интегралу
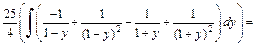
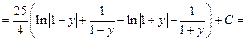
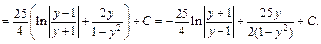
Возвращаемся к заданной переменной, заменяем y на sin t, где 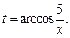 Тогда
Тогда
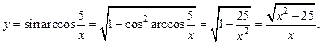
Получаем:
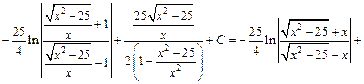
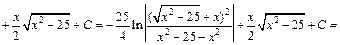
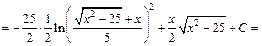
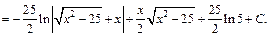
Присоединяя 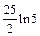 к произвольной постоянной С, получаем:
к произвольной постоянной С, получаем:
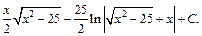
3-й способ. Запишем подынтегральное выражение в виде дифференциального бинома (19.32)
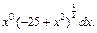
Тогда 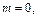
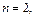
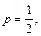
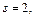
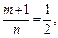
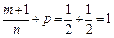 – целое число. Следовательно, имеем третий случай интегрируемости дифференциального бинома. Используем подстановку
– целое число. Следовательно, имеем третий случай интегрируемости дифференциального бинома. Используем подстановку 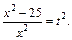 Тогда
Тогда 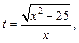
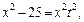
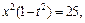
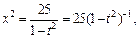
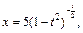
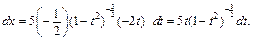
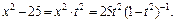
Интеграл преобразуется к виду
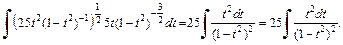
Для вычисления последнего интеграла применим формулу (19.20) интегрирования по частям.
Положим 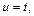
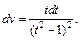 Тогда
Тогда 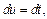
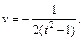 Получаем:
Получаем:
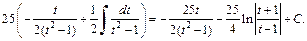
Подставляем 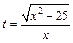 и после преобразований получаем ответ:
и после преобразований получаем ответ:
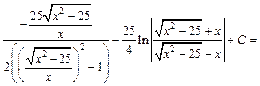
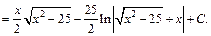
Дата добавления: 2015-09-29; просмотров: 2736;
