Регрессионный анализ. 6 страница
4.10.1 Интерпретация результатов.
Адекватная линейная модель, имеет вид полинома первой степени. Коэффициенты полинома являются частными производными функции отклика по соответствующим переменным. Их геометрический смысл – тангенсы углов наклона гиперплоскости к соответствующей оси. Больший по абсолютной величине коэффициент соответствует большему углу наклона и, следовательно, более существенному изменению параметра оптимизации при изменении данного фактора.
До сих пор мы употребляли абстрактный математический язык. Перевод модели на язык экспериментатора называется интерпретацией модели.
Задача интерпретации весьма сложна. Ее решают в несколько этапов. Первый этап состоит в следующем. Устанавливается, в какой мере каждый из факторов влияет на параметр оптимизации. Величина коэффициента регрессии – количественная мера этого влияния. Чем больше коэффициент, тем сильнее влияет фактор. О характере влияния факторов говорят знаки коэффициентов. Знак плюс свидетельствует о том, что с увеличением значения фактора растет величина параметра оптимизации, а при знаке минус – убывает. Интерпретация знаков при оптимизации зависит от того, ищем ли мы максимум или минимум функции отклика. Если 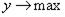 , то увеличение значений всех факторов, коэффициенты которых имеют знак плюс, благоприятно, а имеющих знак минус – неблагоприятно. Если же
, то увеличение значений всех факторов, коэффициенты которых имеют знак плюс, благоприятно, а имеющих знак минус – неблагоприятно. Если же 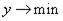 то, наоборот, благоприятно увеличение значений тех факторов, знаки коэффициентов которых отрицательны.
то, наоборот, благоприятно увеличение значений тех факторов, знаки коэффициентов которых отрицательны.
Далее выясняется, как расположить совокупность факторов в ряд по силе их влияния на параметр оптимизации. Факторы, коэффициенты которых не значимы, конечно не интерпретируются. Можно сказать только, что при данных интервалах варьирования и ошибке воспроизводимости они не оказывают существенного влияния на параметр оптимизации.
Изменение интервалов варьирования приводит к изменению коэффициентов регрессии. Абсолютные величины коэффициентов регрессии увеличиваются с увеличением интервалов. Инвариантными к изменению интервалов остаются знаки линейных коэффициентов регрессии. Однако и они изменяться на обратные, если при движении но градиенту мы «проскочим» экстремум.
В некоторых задачах представляет интерес построение уравнения регрессии для натуральных значений факторов. Уравнение для натуральных переменных можно получить, используя формулу перехода. Коэффициенты регрессии изменятся. При этом пропадает возможность интерпретации влияния факторов по величинам и знакам коэффициентов регрессии. Вектор-столбцы натуральных значений переменных в матрице планирования уже не будут ортогональными, коэффициенты определяются зависимо друг от друга. Если же поставлена задача получения интерполяционной формулы для натуральных переменных, такой прием допустим.
Теперь мы получили основу для перехода к следующему этапу. На основе априорных сведений обычно имеются некоторые представления о характере действия факторов. Источниками таких сведений могут служить теория изучаемого процесса, опыт работы с аналогичными процессами или предварительные опыты и т.д.
Если, например, ожидается, что с ростом температуры должно происходить увеличение параметра оптимизации, а коэффициент регрессии имеет знак минус, то возникает противоречие. Возможны две причины возникновения такой ситуации: либо в эксперименте допущена ошибка, и он должен быть подвергнут ревизии, либо неверны априорные представления. Нужно иметь в виду, что эксперимент проводится в локальной области факторного пространства и коэффициент отражает влияние фактора только в этой области. Заранее неизвестно, в какой мере наивно распространить результат на другие области. Теоретические же представления имеют обычно более общий характер. Кроме того, априорная информация часто основывается на однофакторных зависимостях. При переходе к многофакторному пространству ситуация может изменяться. Поэтому мы должны быть уверены, что эксперимент проведен корректно. Тогда для преодоления противоречия можно выдвигать различные гипотезы и проверять их экспериментально.
В тех, довольно редких, случаях, когда имеется большая априорная информация, позволяющая выдвигать гипотезы о механизме явлений, можно перейти к следующему этапу интерпретации. Он сводится к проверке гипотез о механизме явлений и выдвижению новых гипотез.
Получение информации о механизме явлений не является обязательным в задачах оптимизации, но возможность такого рода следует использовать. Здесь особое внимание приходится уделять эффектам взаимодействия факторов. Как их интерпретировать?
Пусть в некоторой задаче взаимодействие двух факторов значимо и имеет положительный знак. Это свидетельствует о том, что одновременное увеличение, как и одновременное уменьшение, значений двух факторов приводит к увеличению параметра оптимизации (без учета линейных эффектов).
Интерпретация эффектов взаимодействия не так однозначна, как линейных эффектов. В каждом случае имеется дна варианта. Какому из вариантов отдавить предпочтение? Прежде всего, нужно учесть знаки линейных эффектов соответствующих факторов. Если эффект взаимодействия имеет знак плюс и соответствующие линейные эффекты отрицательны, то выбор однозначен: сочетание –1 и –1. Однако возможен случай, когда знаки линейных эффектов различны. Тогда приходится учитывать численные значения коэффициентов и жертвовать самым малым эффектом.
Иногда приходится учитывать технологические соображения: например, эксперимент в одной области факторного пространства дороже (или труднее), чем в другой.
Упомянем еще об интерпретации эффектов взаимодействия высоких порядков. Если значимым оказался эффект взаимодействия трех факторов, например 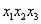 , то его можно интерпретировать следующим образом. Этот эффект может иметь знак плюс, если отрицательные знаки будут у четного числа факторов (ноль или любые два). Знак минус будет, если нечетное число факторов имеет знак минус (все три или любой один). Это правило распространяется на взаимодействия любых порядков. Пользуются еще таким приемом: произведение двух факторов условно считают одним фактором и сводят трехфакторное взаимодействие к парному и т.д.
, то его можно интерпретировать следующим образом. Этот эффект может иметь знак плюс, если отрицательные знаки будут у четного числа факторов (ноль или любые два). Знак минус будет, если нечетное число факторов имеет знак минус (все три или любой один). Это правило распространяется на взаимодействия любых порядков. Пользуются еще таким приемом: произведение двух факторов условно считают одним фактором и сводят трехфакторное взаимодействие к парному и т.д.
Мы сказали, что интерпретация результатов – это перевод с одного языка на другой. Такой перевод обеспечивает взаимопонимание между статистиком и экспериментатором, работающим совместно над задачами оптимизации. Интерпретация уравнения регрессии важна не только для понимания процесса, но и для принятия решений при оптимизации.
4.10.2 Принятие решений после построения модели процесса.
Нам придется принимать решения в сложных ситуациях. Решения зависят от числа факторов, дробности плана, цели исследования (достижение оптимума, построение интерполяционной формулы) и т.д. Количество возможных решений по примерной оценке достигает нескольких десятков тысяч. Поэтому будем рассматривать только наиболее часто встречавшиеся случаи и выделим «типичные» решения. Положение здесь сложнее, чем в случае принятия решений о выборе основного уровня и интервалов варьирования факторов, где удалось рассмотреть все варианты. Ситуации будем различать по адекватности и неадекватности модели, значимости и незначимости коэффициентов регрессии в модели, информации о положении оптимума.
Обсудим сначала принятие решения для адекватного линейного уравнения регрессии.
Линейная модель адекватна. Здесь возможны 3 варианта.
1. Все коэффициенты регрессии значимы.
2. Часть коэффициентов регрессии значима, часть незначима.
3. Все коэффициенты регрессии незначимы.
В каждом варианте оптимум может быть близко, далеко или о его положении нет информации (неопределенная ситуация).
Рассмотрим первый вариант.
Если область оптимума близка, возможны три решения: окончание исследования, переход к планам второго порядка и движение по градиенту.
Переход к планированию второго порядка дает возможность получить математическое описание области оптимума и найти экстремум.
Движение по градиенту используется при малой ошибке опыта, поскольку на фоне большой ошибки трудно установить приращение параметра оптимизации.
Решение при неопределенной ситуации или удаленной области оптимума одно и то же: движение по градиенту.
Второй вариант – часть коэффициентов регрессии значима, часть незначима. Движение по градиенту наиболее эффективно, если коэффициенты значимы. Поэтому выбираются решения, реализация которых приводит к получению значимых коэффициентов. На этом этапе важно выдвинуть гипотезы, объясняющие незначимость эффектов. Это может быть и неудачный выбор интервалов варьирования, и включение (из осторожности) факторов, не влияющих на параметр оптимизации, и большая ошибка опыта, и т.д. Решение зависит от того, какую гипотезу мы предпочитаем.
Если, например, выдвинута первая гипотеза, то возможно такое решение: расширение интервалов варьирования по незначимым факторам и постановка новой серии опытов. Изменение интервалов варьирования иногда сочетают с переносом центра эксперимента в точку, соответствующую условиям наилучшего опыта. Невлияющие факторы стабилизируются и исключаются из дальнейшего рассмотрения. Другие возможные решения для получения значимых коэффициентов: увеличение числа параллельных опытов и достройка плана. Увеличение числа параллельных опытов приводит к уменьшению дисперсии воспроизводимости и соответственно дисперсии коэффициентов регрессии. Опыты могут быть повторены либо во всех точках плана, либо в некоторых.
Достройка плана осуществляется несколькими способами.
1. Методом «перевала» – у исходной реплики изменяют знаки на обратные. В этом случае основные эффекты оказываются не смешанными с парными эффектами
2. Переходом к полному факторному эксперименту.
3. Переходом к реплике меньшей дробности.
4. Переходом к плану второго порядка (если область оптимума близка).
Реализация любого из этих решений требует значительных экспериментальных усилий. Поэтому иногда можно и не следовать строго правилу «двигайтесь по всем факторам», а пойти на некоторый риск и двигаться только по значимым факторам.
Наконец, если область оптимума близка, то возможно принятие таких же решений, как и в случае значимости всех коэффициентов регрессии.
Рассмотрим последний случай: линейная модель адекватна, все коэффициенты регрессии незначимы (кроме b0). Чаще всего это происходит вследствие большой ошибки эксперимента или узких интервалов варьирования. Поэтому возможные решения направлены, прежде всего, на увеличение точности эксперимента и расширение интервалов варьирования. Увеличение точности может достигаться двумя путями: благодаря улучшению методики проведения опытов или вследствие постановки параллельных опытов.
Если область оптимума близка, то возможно также окончание исследования.
В заключение приведем блок-схему (рисунок 4.15) принятия решения в задаче определения оптимальных условий, линейная модель адекватна. В блок-схеме пунктирными линиями обведены ситуации, сплошными линиями – принимаемые решения.
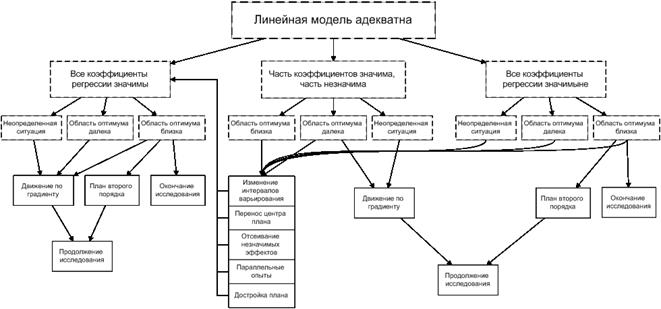
Рисунок 4.15 – Линейная модель адекватна
Линейная модель неадекватна. Если линейная модель неадекватна, значит не удается аппроксимировать поверхность отклика плоскостью. Формальные признаки (кроме величины F-критерия), по которым можно установить неадекватность линейной модели, следующие.
1.Значимость хотя бы одного из эффектов взаимодействия.
2.Значимость суммы коэффициентов регрессии при квадратичных членах 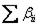 . Оценкой этой суммы служит разность между b0 и значением зависимой переменной в центре плана y0. Если разность превосходит ошибку опыта, то гипотеза о незначимости коэффициентов при квадратичных членах не может быть принята. Однако надо
. Оценкой этой суммы служит разность между b0 и значением зависимой переменной в центре плана y0. Если разность превосходит ошибку опыта, то гипотеза о незначимости коэффициентов при квадратичных членах не может быть принята. Однако надо
учесть, что сумма может быть незначима, и при значимых квадратичных эффектах, если они имеют разные знаки.
Для неадекватной модели мы не будем делать различия между случаями значимых и незначимых линейных коэффициентов регрессии, поскольку решения для них обычно совпадают.
Решения, принимаемые для получения адекватной модели: изменение интервалов варьирования факторов, перенос центра плана, достройка плана.
Наиболее распространенный прием – изменение интервалов варьирования. Он, конечно, требует постановки новой серии опытов. Иногда отказываются от построения адекватной модели, чтобы ценой нескольких опытов проверить возможность движения по градиенту. Это решение нельзя считать достаточно корректным. Движению по градиенту обычно предшествует оценка кривизны поверхности отклика (по сумме коэффициентов при квадратичных членах) и сопоставление величин линейных эффектов и эффектов взаимодействия. Если вклад квадратичных членов и эффектов взаимодействия невелик, то решение о движении по градиенту представляется возможным.
Еще одно решение: включение в модель эффектов взаимодействия и движение с помощью неполного полинома второго порядка. Этот прием связан с получением и анализом уравнений второго порядка. Направление градиента будет меняться от точки к точке.
Если область оптимума близка, то возможны варианты окончания исследования и
перехода к построению плана второго порядка.
На рисунке 4.16 приведена блок-схема принятия решений в задаче оптимизации для случая, когда линейная модель неадекватна.
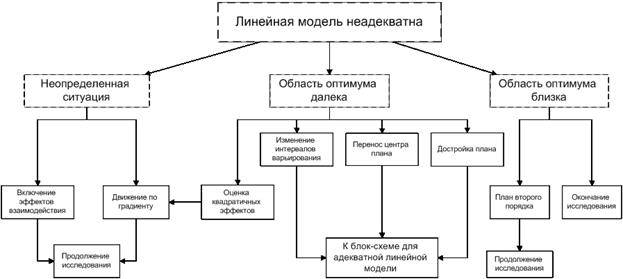
Рисунок 4.16 – Линейная модель неадекватна
Особый случай возникает при использовании насыщенных планов. При значимости всех коэффициентов регрессии ничего нельзя сказать об адекватности или неадекватности модели. Движение по градиенту в такой ситуации показывает правильность предположения, что коэффициенты регрессии являются оценками для линейных эффектов.
4.10.3 Построение интерполяционной формулы, линейная модель неадекватна.
Первое, что следует сделать ври решении этой задачи, – включить в уравнение эффекты взаимодействия. Конечно, такое решение возможно, если был применен ненасыщенный план. После добавления эффектов взаимодействия может не хватить степеней свободы для проверки гипотезы адекватности и потребуется реализация ещё двух-трех опытов внутри области эксперимента.
Все остальные способы построения интерполяционной формулы связаны с необходимостью проведения новых опытов. Один из них – достройка плана. Используются все те же приемы, что и при устранении незначимости коэффициентов регрессии: метод «перевала», достройка до полного факторного эксперимента, до дробной реплики, для которой ранее смешанные эффекты становятся «чистыми», достройка до плана второго порядка.
Наконец, если не удалось все же получить адекватную модель, то остается разбить область эксперимента на несколько подобластей и описать отдельно каждую из них. Это требует уменьшения интервалов варьирования факторов.
Приведем блок-схему принятия решений в задаче построения интерполяционной формулы для случая, когда лилейная модель неадекватна. Если линейная модель адекватна, то задача решена.
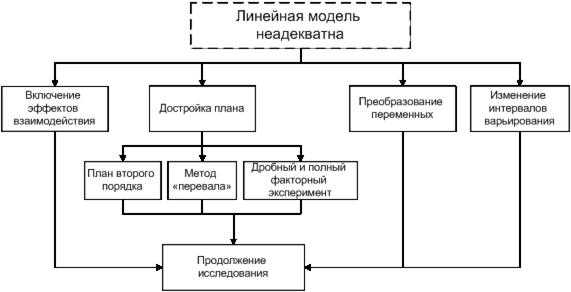
Рисунок 4.17 - Блок-схема принятия решений в задаче построения интерполяционной формулы для случая, когда лилейная модель неадекватна
Вопросы
1. Структура экспериментального исследования.
2. Требования к эксперименту по оценке прецизионности. Рандомизация.
3. Проверка воспроизводимости эксперимента. Отсев грубых погрешностей.
4. Дисперсия воспроизводимости. Проверка однородности дисперсий.
5. Обработка результатов эксперимента. Метод наименьших квадратов.
6. Проверка адекватности модели.
7. Проверка значимости коэффициентов.
8. Принятие решений после построения модели. Интерпретация результатов.
9. Принятие решений после построения модели процесса. Линейная модель адекватна.
10. Принятие решений после построения модели процесса. Линейная модель неадекватна.
Литература
Раздел 5 Измерения, их виды и классы
5.1 Основы теории ошибок измерений
5.1.1 Виды измерений и погрешностей
Измерение - это определение значения физической величины опытным путём при помощи специальных технических средств.
На практике задача измерения включает не только определение числа, выражающего отношение измеряемой величины к общепринятой единице измерения, но и определение при этом допущенной погрешности.
Непосредственный процесс измерения состоит из наблюдения и отсчёта.
Цель наблюдения - фиксация факта наступления какого-либо определённого события. После наступления ожидаемого события производится считывание показания прибора со шкалы лимба или цифрового табло, определение массы эталонного вещества (гирь) и т.д.
Виды измерений классифицируются:
- по способу получения результата (прямые и косвенные);
- по методу измерений (абсолютные, относительные и пороговые);
- по условиям измерений (равноточные, неравноточные);
- по степени достаточности измерений (необходимые, избыточные).
При прямыхизмерениях измеряется непосредственно исследуемая величина.
При косвенныхизмерениях исследуемая величина измеряется как функция по результатам измерения других величин.
Например, ускорение автомобиля при разгоне определяется по результатам измерения расстояния и времени разгона; вычисление плотности - по массе и объему.
Абсолютныеизмерения - это прямые измерения в единицах измеряемой величины.
Δх = х – а, (5.1)
где х - результат измерения;
а - истинное значение.
Относительныеизмерения представляют собой отношения измеряемой величины к величине играющей роль единицы или к величине, принимаемой за исходную. Например, влажность воздуха в % по отношению к полному его водонасыщению.
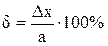 . (5.2)
. (5.2)
При пороговыхизмерениях фиксируется только факт нахождения величины в одностороннем или двухстороннем допуске (по принципу "да/нет").
Равноточныеизмерения проводятся в одинаковых условиях одними и теми же измерительными приборами и с одинаковой степенью тщательности. При этом в ряду измерений нельзя отдать предпочтение какому-либо одному или нескольким значениям.
Неравноточныеизмерения не отвечают указанным выше требованиям.
Избыточныеизмерения имеют по сравнению с необходимыми большее число измерений либо большую точность, содержат среди измерений зависимые, т. е. дают избыточную информацию.
Надежность результатов исследования в значительной степени зависит от точностиизмерений.
Под точностьюизмерений понимают степень соответствия результата измерения действительному значению измеряемой величины.
В зависимости от точности результатов можно выделить три класса измерений:
1) эталонные, результат которых должен иметь максимально возможную точность при достигнутом уровне техники и науки (измерения физических констант);
2) контрольно-поверочные, при которых ошибка результата не превышает заранее заданного допуска (измерения в поверочных или контрольно-измерительных лабораториях при поверке приборов);
3) технические, ошибка результатов которых определяется характеристиками измерительного комплекса.
Снять показания с прибора — не значит только измерить. Необходимо еще оценить ошибки (погрешности) измерений.
Погрешностьизмерения — это отклонение результата измерения от истинного значения измеряемой величины.
Под истинным значением измеряемой величины принято считать:
- среднюю арифметическую величину ряда измерений;
- известное эталонное значение;
- величину, полученную в результате более точных (не менее чем на порядок) измерений.
Основные источники ошибок:
первый источникзаключен в датчике, который неправильно реагирует на измеряемую величину. Например, если тензосопротивление плохо наклеено на упругий элемент, то деформация его решетки не будет соответствовать деформации упругого элемента;
второй источник - измерительное устройство, в котором возможны погрешности из-за неправильного функционирования его механических или электрических элементов;
третий источник — сам наблюдатель, который из-за неопытности или усталости неправильно считывает показания прибора.
Кроме того, ошибки в измерении могут возникнуть из-за влияния измерительного устройства на объект измерения (например, при разрушающем методе контроля), влияния окружающей среды (температура, загазованность и т. п.), методических погрешностей, допущенных экспериментатором.
Эти источники ошибок приводят к появлению трех типов ошибок (погрешностей): случайных, систематических и грубых.
Случайнаяпогрешность - это погрешность, которая в отдельных измерениях может принимать случайные, заранее конкретно неизвестные значения. Случайные погрешности обязаны своим происхождением ряду как объективных, так и субъективных факторов, действие которых неодинаково в каждом опыте и не может быть учтено. Случайные погрешности различаются в отдельных измерениях, сделанных в одинаковых условиях одними и теми же измерительными прибора ми. Исключить случайные погрешности нельзя. Можно только оценить их значение.
Случайные погрешности определяются по законам теории ошибок, основанной на теории вероятностей.
Систематическая погрешность - это погрешность, вызванная факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений с помощью одних и тех же измерительных приборов.
В качестве примера систематической ошибки рассмотрим случай взвешивания на чашечных весах с помощью неточных гирь. Если взятая нами гиря имеет ошибку, скажем 0,1 г, то вес тела (пусть 1000 г) будет завышенным (или заниженным) на эту величину, и чтобы получить верное значение, необходимо учесть эту ошибку, прибавив к полученному весу (или вычтя из него) 0,1 г, Р = (1000±0,1) г.
Грубаяпогрешность или промах вызывается просчетом экспериментатора или неисправностью средств измерения, или резко изменившимися внешними условиями.
Грубые погрешности приводят к явному искажению результата, поэтому их надо исключить из общего числа измерений.
5.1.2 Случайные погрешности и их распределение.
Для того, чтобы выявить случайную погрешность измерений, необходимо повторить измерение несколько раз. Если каждое измерение дает заметные от других результаты, мы имеем дело с ситуацией, когда случайная погрешность играет существенную роль.
Наиболее вероятным значением измеряемой величины из серии измерений является ее среднее значение. Рассеивание измеряемой величины относительно ее среднего значения определяется величиной средней квадратической погрешности отдельного измерения.
Пусть в измерительном эксперименте в результате независимых и равноточных измерений постоянной величины а получены значения xl,x2,...,xn. Абсолютные погрешности (5.1) рассматривают как случайные величины. При этом независимость измерений понимается как взаимная независимость случайных величин Δхi, а равноточность - как подчинение величин Δхi, одному и тому же закону распределения (к тому же измерения сделаны одним и тем же методом и с одинаковой степенью тщательности).
В качестве оценки неизвестной величины а по данным измерений обычно берут среднее арифметическое хрезультатов измерений:
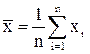 , (5.3)
, (5.3)
Дисперсия отдельных измерений
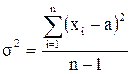 , (5.4)
, (5.4)
чаще всего неизвестна, и для ее оценки используется величина
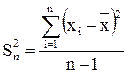 , (5.5)
, (5.5)
Среднюю квадратическую (стандартную) погрешность а (СКО) находятся по формуле (5.6).
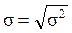 , (5.6)
, (5.6)
для ее оценки вычисляется величина
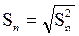 , (5.7)
, (5.7)
В действительности мы всегда вычисляем не σ, Sn, которые тем ближе к σ, чем больше n:
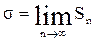 , (5.8)
, (5.8)
Обычно принимается, что погрешности подчиняются нормальному закону распределения случайных величин. При этом предполагается:
1) погрешности измерений могут принимать непрерывный ряд значений;
2) при большом числе наблюдений погрешности равных значений, но разных знаков встречаются одинаково часто;
3) частота появления погрешностей уменьшается с увеличением величин погрешностей. Иначе говоря, большие ошибки наблюдаются реже, чем малые.
Эти предположения приводят к закону распределения погрешностей, описываемому формулой Гаусса:
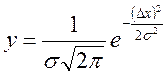 , (5.9)
, (5.9)
Форма кривых Гаусса зависит от величин σ. Чем больше σ, тем больше рассеивание случайной погрешности. На рисунке 5.1 представлены кривые Гаусса для трех значений σ. С помощью этих кривых можно установить, насколько часто должны появляться ошибки той или иной величины.
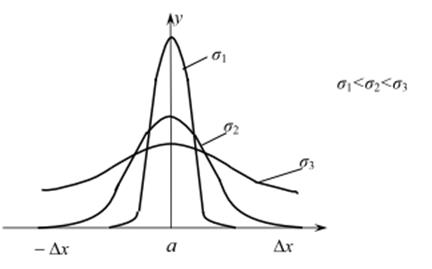
Рисунок 5.1 – Кривые нормального распределения
Известно, что под кривой распределения в пределах по оси абсцисс от - σ до + σзаключено 68,3% всей площади; в пределах от - 2σдо +2σ- 95,5%, в пределах от -3σдо + 3σ- 99,7%, (рисунок 5.2).
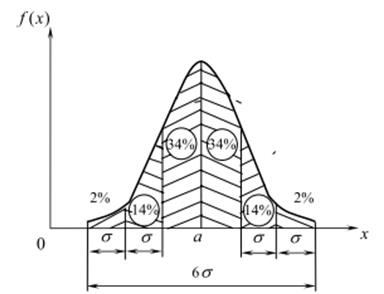
Рисунок 5.2 – Значения вероятностей для нормального закона распределения по диапазонам стандартных отклонений
Отсюда свойство нормального закона распределения случайных величин - рассеивание случайной величины в основном (с вероятностью Р=0,997) укладывается на участке а ± 3σ, где а -математическое ожидание.
Следовательно, зная σ и а, можно приблизительно указать интервал ее практически возможных значений (размах). Такой способ оценки диапазона значений случайной величины называется правилом "трех сигм".
5.1.3 Выборочное среднее как оценка истинного значения измеряемой величины
Выполняя любое измерение, мы заранее предполагаем, что существует точноеистинное значение, измеряемой величины хист. Однако из-за неизбежных ошибок при измерениях действительные результаты эксперимента хi обычно заметно отличаются от хист, поэтому результат измерения любой физической величины при наличии случайной погрешности ведет себя как некоторая случайная величина. Иногда, и сама, измеряемая величина, даже в отсутствии ошибок измерения, может меняться случайным образом. Тогда в роли истинного значения, которое нам нужно отыскать в результате эксперимента, обычно выступает истинное среднее, то есть среднее значение физической величины за большой промежуток времени.
Истинная абсолютная погрешностьизмеряемой величины
Δхi = хi - хист, (5.10)
где хi – действительный результат измерения;
хист - истинное значение измеряемой величины.
Выборочное среднее 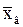 может быть использовано в качестве оценки истинного значения измеряемой величины хист.
может быть использовано в качестве оценки истинного значения измеряемой величины хист.
Дата добавления: 2017-12-05; просмотров: 682;
