Среднее квадратическое отклонение можно использовать для оценки точности измерений.

Если число измерений n достаточно велико (на практике: n>30), то случайная величина удовлетворяет условиям центральной предельной теоремы и подчиняется нормальному закону распределения с центром х_ист и неизвестным нам средним квадратическим отклонением σ.

Центральные предельные теоремы (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

Зададим предельную доверительную погрешность δ = 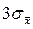и воспользуемся правилом трех сигм для нормального распределения:

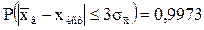. (5.13)

Вероятность того, что х_ист отклоняется от произвольного значения величины 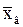на расстояние не более чем 3σ( 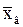) равна 0,9973 (или 99,73%).

Таким образом, с вероятностью 0,9973, происходит событие, состоящее в том, что истинное значение измеряемой величины попадает в доверительный интервал (5.14)

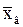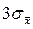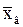- ≤ - х_ист ≤ 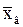+ 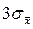. (5.14)

С вероятностью 0,9973 выполняется условие (5.15)

х_ист = 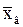+ 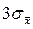. (5.15)

Вывод:поскольку в 99,73% случаев истинное значение измеряемой величины х_ист отклоняется от выборочного среднего 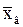не более чем на 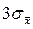, то для оценки точности измерений мы можем использовать величину .

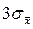5.1.5 Доверительный интервал и доверительная вероятность.

Обозначим истинное значение измеряемой величины через х_ист, погрешность из­мерения этой величины - Δх. Среднее арифметическое значение, полученное в результате измерений, будет 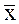. Пусть γозначает вероятность того, что результат измерений отличается от истинного значения на величину, не большую, чем Δх. Это принято записывать в виде

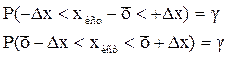. (5.16)

Вероятность γназывается доверительной вероятностью, или коэффициен­том надежности. Интервал значений от х_ист-Δх до х_ист+Δх называется доверитель­ным интервалом.

Выражение (5.10) означает, что с вероятностью, равной γ, истинное значение измеряемой величины не выходит за пределы доверительного интервала от х_ист-Δх до х_ист+Δх. Разумеется, чем большей надежности мы требуем, тем большим полу­чается соответствующий доверительный интервал, и, наоборот, чем больший до­верительный интервал задаем, тем вероятнее, что результаты измерений не вый­дут за его пределы.

Итак, для характеристики величины случайной ошибки необходимо задать два числа, а именно: величину самой ошибки (или доверительного интервала) и вели­чину доверительной вероятности.

Указание одной только величины ошибки без указания соответствующей ей доверительной вероятности в значительной мере лишено смысла, так как при этом не знаем, сколь надежны наши данные. Знание доверительной вероятности позволяет оценить степень надежности полученного результата. Необходимая степень его надежности опять-таки задается характером производимых измерений. Более высокая степень надежности, требуемая при от­ветственных измерениях, означает, что при их производстве нужно выбирать большой (в долях с) доверительный интервал. Иначе говоря, для получения той же величины ошибки Δх следует производить измерения с большей точностью, т. е. нужно тем или иным способом уменьшить в соответствующее число раз величину σ. Одна из возможностей такого увеличения состоит в многократном по­вторении измерений.

При обычных измерениях можно ограничиться доверительной вероятностью 0,9 или 0,95.

Для измерений, по условиям которых требуется чрезвычайно высокая степень надежности, иногда задают доверительную вероятность 0,997. Большая величина доверительной вероятности в подавляющем большинстве измерительных задач не требуется.

Удобство применения стандартной ошибки в качестве основного численного выражения погрешности наблюдений заключается в том, что этой величине соот­ветствует вполне определенная доверительная вероятность, равная 0,68. (Здесь и дальше полагаем, что ошибки распределены по нормальному закону). Для любой величины доверительного интервала по формуле Гаусса может быть рассчитана соответствующая доверительная вероятность. Эти вычисления были проделаны, и их результаты сведены в таблицу (Приложение 4).