Методы уточнения корней

Численные методы

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит потому, что искомое решение обычно не выражается в элементарных или других известных функциях. Поэтому большое значение приобрели численные методы.

Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами. В зависимости от сложности задачи, заданной точности, применяемого метода может потребоваться огромное количество действий, и здесь без быстродействующего компьютера не обойтись.

Решение, полученное численным методом, обычно является приближенным, т. е. содержит некоторую погрешность. Источниками погрешности приближенного решения задачи являются:

- погрешность метода решения;

- погрешности округлений в действиях над числами.

Погрешность метода вызвана тем, что численным методом обычно решается другая, более простая задача, аппроксимирующая (приближающая) исходную задачу. В ряде случаев численный метод представляет собой бесконечный процесс, который в пределе приводит к искомому решению. Процесс, прерванный на некотором шаге, дает приближенное решение.

Погрешность округления зависит от количества арифметических действий, выполняемых в процессе решения задачи. Для решения одной и той же задачи могут применяться различные численные методы. Чувствительность к погрешностям округления существенно зависит от выбранного метода.

Решение нелинейных уравнений

Постановка задачи

Решение нелинейных уравнений с одним неизвестным является одной из важных математических задач, возникающих в различных разделах физики, химии, биологии и других областях науки и техники.

В общем случае нелинейное уравнение с одним неизвестным можно записать:

f ( x) = 0 ,

где f ( x) – некоторая непрерывная функция аргумента x.

Всякое число x₀ , при котором f (x₀) ≡ 0, называется корнем уравнения f ( x) = 0.

Методы решения нелинейных уравнений делятся на прямые (аналитические, точные) и итерационные. Прямые методы позволяют записать решение в виде некоторого соотношения (формулы). При этом значения корней могут быть вычислены по этой формуле за конечное число арифметических операций. Подобные методы развиты для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. Даже для алгебраического уравнения выше четвертой степени не удается получить аналитического решения в виде формулы с конечным числом арифметических действий. Во всех таких случаях приходится обращаться к численным методам, позволяющим получить приближенные значения корней с любой заданной точностью.

При численном подходе задача о решении нелинейных уравнений разбивается на два этапа: локализация (отделение) корней, т.е. нахождение таких отрезков на оси x, в пределах которых содержится один единственный корень, и уточнение корней, т.е. вычисление приближенных значений корней с заданной точностью.

Локализация корней

Для отделения корней уравнения f ( x) = 0 необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке [ a, b] имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке.

Если функция f ( x) непрерывна на отрезке [ a, b], а на концах отрезка её значения имеют разные знаки, т. е.

f(a) × f(b) < 0 ,

то на этом отрезке расположен, по крайней мере, один корень.

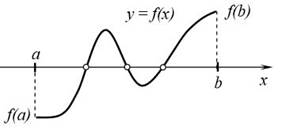
Рис 1. Отделение корней. Функция f( x) не монотонна на отрезке [ a, b].

Это условие, как видно из рисунка (1), не обеспечивает единственности корня. Достаточным дополнительным условием, обеспечивающем единственность корня на отрезке [a, b] является требование монотонности функции на этом отрезке. В качестве признака монотонности функции можно воспользоваться условием постоянства знака первой производной f ′( x) .

Таким образом, если на отрезке [ a, b] функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень.

Воспользовавшись этим критерием, можно отделить корни аналитическим способом, находя интервалы монотонности функции.

Отделение корней можно выполнить графически, если удается построить график функции y = f ( x) . Например, график функции на рисунке (1) показывает, что эта функция на интервале [a, b] может быть разбита на три интервала монотонности и на этом интервале у нее существуют три корня.

Отделение корней можно также выполнить табличным способом. Допустим, что все интересующие нас корни уравнения (2.1) находятся на отрезке [A, B]. Выбор этого отрезка (интервала поиска корней) может быть сделан, например, на основе анализа конкретной физической или иной задачи.

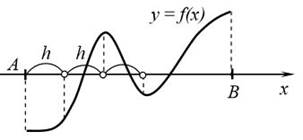
Рис. 2. Табличный способ локализации корней.

Будем вычислять значения f ( x) , начиная с точки x = A , двигаясь вправо с некоторым шагом h (рис. 2). Как только обнаруживается пара соседних значений f ( x) , имеющих разные знаки, так соответствующие значения аргумента x можно считать границами отрезка, содержащего корень.

Надежность табличного способа отделения корней уравнений зависит как от характера функции f ( x) , так и от выбранной величины шага h. Действительно, если при достаточно малом значении h ( h <<| B − A |) на границах текущего отрезка [ x, x + h] функция f ( x) принимает значения одного знака, то естественно ожидать, что уравнение f ( x) = 0 корней на этом отрезке не имеет. Однако, это не всегда так: при несоблюдении условия монотонности функции f ( x) на отрезке [ x, x + h] могут оказаться корни уравнения (рис. 3а).

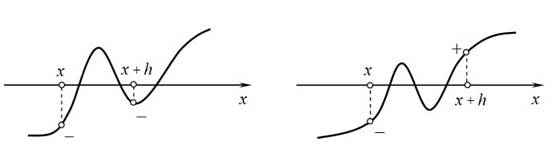
Рис 3а Рис 3б

Также несколько корней на отрезке [x, x + h] могут оказаться и при выполнении условия f(x) × f(x+h) < 0 (рис. 3б). Предвидя подобные ситуации, следует выбирать достаточно малые значения h.

Отделяя таким образом корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность этого значения не будет превосходить половины шага поиска ( h/2). Уменьшая шаг в окрестности каждого корня, можно, в принципе, повысить точность отделения корней до любого наперед заданного значения. Однако такой способ требует большого объема вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять поиск корней, подобный метод не годится для уточнения корней и используется только для отделения (локализации) корней, т.е. определения начальных приближений к ним. Уточнение корней проводится с помощью других, более экономичных методов.

Уточнение корней

На данном этапе задача состоит в получении приближенного значения корня, принадлежащего отрезку [ a, b], с заданной точностью (погрешностью) ε. Это означает, что вычисленное значение корня x^~ должно отличаться от точного x₀ не более чем на величину ε:

| x₀ – x^~| £ ε

Процедура численного определения приближенных значений корней нелинейных уравнений, как правило, состоит в выборе начального приближения к корню x₀ Î[ a, b] и вычислении по некоторой формуле последующих приближений , x₁ x₂ и т.д. Каждый такой шаг называется итерацией, а сами методы уточнения – итерационными методами. В результате итераций получается последовательность приближенных значений корня
x₀ , x₁ , . . . , x_k, . . . , которая называется итерационной последовательностью. Если эти значения с ростом k стремятся к точному значению корня x₀, то говорят, что итерационный процесс сходится :

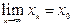
Методы уточнения корней