Метод половинного деления

Считаем, что отделение корней уравнения f ( x) = 0 проведено и на отрезке [ a, b] расположен один корень, который необходимо уточнить с погрешностью ε. В качестве начального приближения корня принимаем середину этого отрезка: c₀ = (a + b) / 2 (рис. 4):

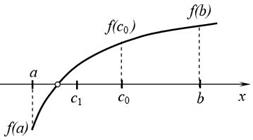
Рис. 4. Метод половинного деления.

Затем исследуем значение функции f ( x) на концах отрезков [ a, c₀ ] и [ c₀ , b] . Тот из отрезков, на концах которого f ( x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка [ a₁ , b₁ ] (на рис. 4 это отрезок [ a, c₀ ]). Вторую половину отрезка [ a, b], на которой f ( x) не меняет знак, отбрасываем. В качестве следующего приближения корня принимаем середину нового отрезка
c₁ = ( a₁ + b₁ ) / 2 и т.д. Таким образом, k-е приближение вычисляется как

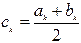
После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k итераций в 2^k раз:

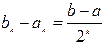
Прекратить итерационный процесс следует, когда будет достигнута заданная точность, т.е. при выполнении условия |x₀ – c_k| < ε

Поскольку корень x₀ принадлежит отрезку [ a_k , b_k ], а c_k – середина этого отрезка, то величина |x₀ – c_k| всегда будет меньше половины длины от резка [ a_k , b_k ] (см. рис. 4):

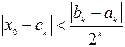
Следовательно, условие |x₀ – c_k| < ε будет выполнено, если

| b_k – a_k | < 2ε

Таким образом, итерационный процесс нужно продолжать до тех пор, пока не будет выполнено условие | b_k – a_k | < 2ε.

В отличие от большинства других методов уточнения, метод половинного деления сходится всегда, т.е. обладает безусловной сходимостью. Кроме этого он чрезвычайно прост, поскольку требует лишь вычисления значений функции f ( x) и, поэтому применим для решения любых уравнений.

Однако метод половинного деления довольно медленный. С каждым шагом погрешность приближенного значения уменьшается в два раза, т.е.

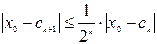
поэтому данный метод является методом с линейной сходимостью.

З а м е ч а н и е . Метод половинного деления не требует знания дополнительной информации о функции на всем интервале [ a, b]. Например, не требуется, чтобы функция была дифференцируема. Даже для разрывных функций рассмотренный метод обладает гарантированной сходимостью. Если на этом интервале существует несколько корней уравнения, один из корней обязательно будет найден.

Метод хорд

Рассматриваемый метод так же, как и метод половинного деления, предназначен для уточнения корня на интервале [ a, b], на концах которого функция f ( x) принимает значения разных знаков. Очередное приближение в отличие от метода половинного деления берем не в середине отрезка, а в точке x , где пересекает ось абсцисс прямая линия (хорда), проведенная через точки А и В (рис. 5).

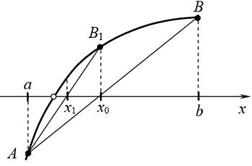
Рис. 5. Метод хорд.

Запишем уравнение прямой, проходящей через точки А и В:

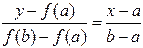
Для точки пересечения прямой с осью абсцисс ( x = x₀ , y = 0) получим уравнение

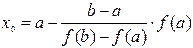
В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух [ a, x₀ ] и [ x₀ , b], на концах которого функция f ( x) принимает значения разных знаков. Для рассматриваемого случая (рис. 5) выбираем отрезок [ a, x₀ ], так как
f(a) × f(x₀) < 0 . Следующая итерация состоит в определении нового приближения x₁ как точки пересечения хорды AB₁ с осью абсцисс и т.д.

Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями станет меньше заданной точности, т.е.

x_k+1 – x_k < ε

З а м е ч а н и е . Метод хорд и метод половинного деления очень похожи. При этом второй их них в ряде случаев дает более быструю сходимость итерационного процесса. Оба метода не требуют знания дополнительной информации о функции на всем интервале [ a, b]. Например, не требуется, чтобы функция была дифференцируема. Даже для разрывных функций рассмотренные методы обладают гарантированной сходимостью.

Метод Ньютона (метод касательных)

Метод Ньютона также предназначен для уточнения корня на интервале [ a, b], на концах которого функция f ( x) принимает значения разных знаков. Но этот метод использует дополнительную информацию о функции f ( x). Как результат он обладают более быстрой сходимостью, но в то же время, применим для более узкого класса функций, и его сходимость не всегда гарантирована.

Отделяя корни функции, следует учесть, что применение метода Ньютона требует, чтобы функция была монотонна и дважды дифференцируема, причем вторая производная f’’(x) на этом интервале не должна менять знак.

Cходимость итерационной последовательности, получаемой в методе Ньютона, зависит от выбора начального приближения x₀ . В общем случае, если задан интервал [ a, b], содержащий корень, и известно, что функция f ( x) монотонна на этом интервале, то в качестве начального приближения x₀ можно выбрать ту границу отрезка [ a, b], где совпадают знаки функции f ( x) и второй производной f’’(x). Такой выбор начального приближения гарантирует сходимость метода Ньютона при условии монотонности функции на отрезке локализации корня.

Пусть нам известно начальное приближение к корню x₀. Проведем в этой точке касательную к кривой y = f ( x) (рис. 6). Эта касательная пересечет ось абсцисс в точке , которую будем рассматривать в качестве следующего приближения.

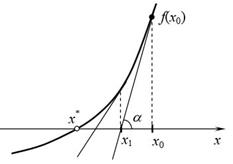
Рис. 6. Метод Ньютона

Значение x₁ легко найти из рисунка:

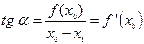
выражая отсюда x₁, получим

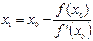
Аналогично могут быть найдены и следующие приближения. Формула для k+1-го приближения имеет вид

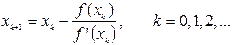
Из этой формулы вытекает условие применимости метода: функция f ( x) должна быть дифференцируемой и f ′ (x) в окрестности корня не должна менять знак.

Для окончания итерационного процесса могут быть использованы условия
f(x_k) < ε или x_k+1 – x_k < ε