Метод прямоугольников
Простейшим методом численного интегрирования является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной суммой:
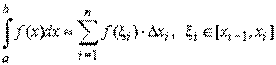
Разобьём интервал интегрирования [a,b] на n равных частей. Обозначим Dхi = h шаг разбиения. Формула прямоугольника применяется к каждому отрезку. В качестве точек xi выбираются левые(xi = хi – 1) или правые (xi = хi ) границы элементарных отрезков Соответственно, для этих двух случаев можно записать формулы метода прямоугольников:
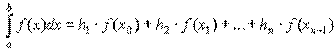
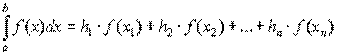
Более точным является вид формулы прямоугольников, использующий значения функции в средних точках элементарных отрезков: точка 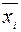 . Таким образом, площадь криволинейной трапеции заменяется суммой прямоугольников с основанием h и высотами, равными значениям функции f(x) в середине оснований
. Таким образом, площадь криволинейной трапеции заменяется суммой прямоугольников с основанием h и высотами, равными значениям функции f(x) в середине оснований 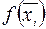 . Получим формулу:
. Получим формулу:
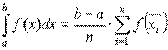 , где
, где 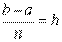 или
или 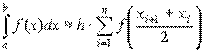
Графическая интерпретация для левых, правых и центральных прямоугольников:
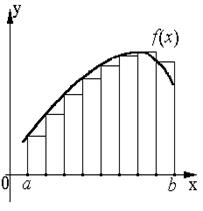
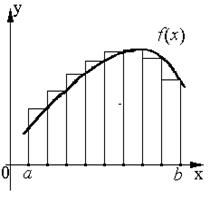
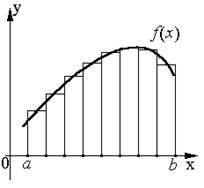
Метод трапеций
Метод трапеций использует линейную интерполяцию, т.е. график функции у=f(х) представляется в виде ломаной, соединяющей точки (хi, уi). В этом случае площадь всей криволинейной трапеции складывается из площадей элементарных прямоугольных трапеций
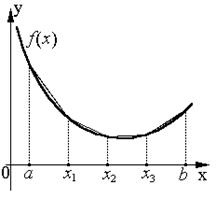
Площадь каждой трапеции определяется по формуле:
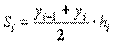 ,
, 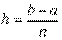 ,
,
где n - число интервалов разбиения. , i=1,2,...,n .
Складывая площади элементарных трапеций, получим формулу трапеций для численного интегрирования:
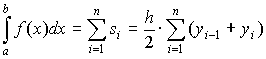 или
или 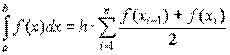
Эти формулы можно представить в виде:
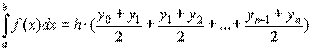 или
или 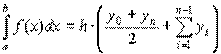
Метод парабол (формула Симпсона)
Метод парабол – метод более точный по сравнению с методами прямоугольников и трапеций. В основе формулы Симпсона лежит квадратичная интерполяция подынтегральной функции на отрезке [a,b] по трем равноотстоящим узлам.
Пусть функция y = f(x) непрерывна на отрезке [a,b] и требуется вычислить определенный интеграл 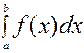
Разобьем интервал интегрирования [a, b] на n элементарных отрезков [x2i-2; x2i],
i = 1, 2, ..., n длины 2h = (b-a)/n точками a = x0 < x2 < x4 < ... < x2n-2 <x2n = b. Пусть точки x2i-1, i = 1, 2, ..., n являются серединами отрезков [x2i-2; x2i], i = 1, 2, ..., n соответственно. В этом случае все «узлы» определяются из равенства xi = a + i×h, i = 1, 2, ..., n.
На каждом интервале [x2i-2; x2i], i = 1, 2, ..., n подынтегральная функция приближается квадратичной параболой y = aix2 + bix + ci, проходящей через точки
(x2i-2;f(x2i-2)), (x2i-1;f(x2i-1)), (x2i;f(x2i))
Это делается для того, чтобы в качестве приближенного значения определенного интеграла 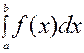 взять
взять 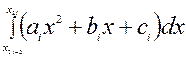 , который можно вычислить по формуле Ньютона-Лейбница.
, который можно вычислить по формуле Ньютона-Лейбница.
Геометрически это выглядит так:
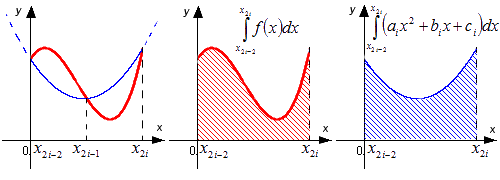
Пусть x2i-2 = 0 (мы всегда можем к этому прийти, проведя соответствующее геометрическое преобразования сдвига для любого i = 1, 2, ..., n).
Можно доказать, что через точки (x2i-2;f(x2i-2)), (x2i-1;f(x2i-1)), (x2i;f(x2i)) проходит только одна квадратичная парабола y = aix2 + bix + ci
Перейдем к нахождению интеграла 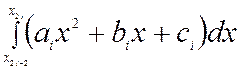
Очевидно:
f(x2i-2) = f(0) = ai×02 + bi×0 + ci
f(x2i-1) = f(h) = ai×h2 + bi×h + ci
f(x2i) = f(2h) = 4ai×h2 +2 bi×h + ci
Используем эти равенства, чтобы осуществить последний переход в следующей цепочке равенств:
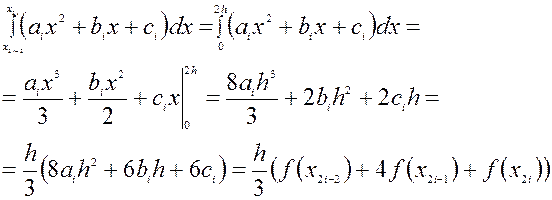
Таким образом, можно получить формулу метода парабол:
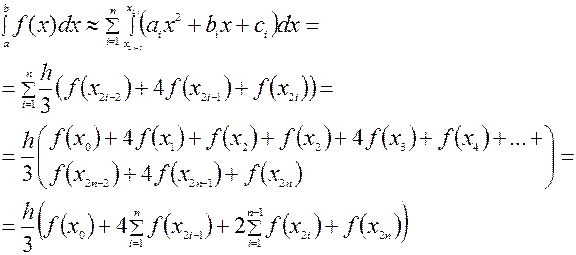
Формула метода Симпсона (парабол) имеет вид:
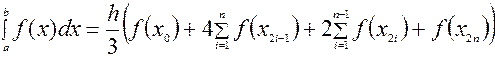

Дата добавления: 2017-09-19; просмотров: 1067;
