Обработка результатов эксперимента.

В конце представляется отчёт; для представления отчёта по теме проводятся эксперименты; данные должны быть в виде формул, экспериментальные данные необходимо обработать. Смысл обработки в том, чтобы выяснить, правильно ли проведён эксперимент.

Существует 2 этапа обработки результата:

1. Выявление связей параметров. Проводится выявление наличия зависимости одного фактора от другого (входные воздействия и отклики). Как правило, общий вид закономерности известен из литературы. Когда имеется много воздействий, проводится специальный вид анализа – корреляционный анализ.

2. Определение погрешностей.

Способ обработки результатов эксперимента:

1. Запись результатов измерения .

2. Вычисление среднего значения из N измерений

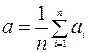
3. Определение погрешности отдельных измерений

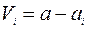
4. Вычисление квадратичной погрешности отдельных измерений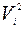

5. Если несколько измерений резко отличаются от остальных, следует проверить, не являются ли они промахами. Эти промахи исключаются и повторяются пункты 1-4

6. Определяется среднеквадратичная погрешность результата серии измерений:

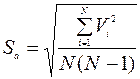
7. Задаётся значение коэффициента надёжности α.

α =0,9; 0,95; 0,99.

8. По надёжности определяется коэффициент Стьюдента t_α(n).

9. Находятся границы доверительного интервала

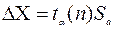
10. Если величина погрешности результата 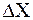оказывается сравнима с величиной приборной погрешности, то в качестве границы доверительного интервала следует взять величину:

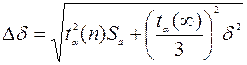
11. Записывается окончательный результат.

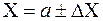
12. Считается относительная погрешность:

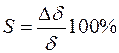
Смысл такой проверки в том, что если измерение проведено корректно, то существует какое-то среднее значение, около которого по Гауссовой кривой и будут распределяться значения результата.

Большинство измерений (с определённым α) будут находиться в интервале ±ΔХ. Если во время измерений не учтена погрешность, то график кривой будет деформирован. Если же построение корректно, то все отклонения значения от истинного значения будут носить случайный характер и распределяется по нормальному закону.

Если сделан вывод, что результат корректен, то можно переходить к следующему этапу – построению регрессионных моделей.

Регрессия – описание экспериментальных данных некоторой зависимостью (формулой) для нахождения численных коэффициентов, которые характеризуют некоторые параметры протекающих в образце процессов. Т.о. экспериментальную кривую мы пытаемся описать какой-то простой кривой.

Измерения бывают прямые и косвенные.

Прямые – на выходе получается измерительный параметр – измерение путём сравнения с образцом.

Косвенные – измерение искомого параметра путём измерения сопутствующего параметра. Косвенные измерения содержат больше ошибок и погрешностей.

У цифрового прибора последняя цифра всегда неверна (она не определяется, а отбрасывается).

Ошибки (погрешности):

1. Систематические – обусловлены какими-либо дефектами прибора или постоянными внешними воздействиями; они присутствуют в приборе всегда; все измерительные периодически проходят поверку; есть специальные правила, нормы, таблицы по данному прибору – о времени поверки и др.

2. Случайные – возникают из-за множества причин; такие ошибки в прямом эксперименте невозможно устранить. Но если число измерений увеличивается в N раз, то погрешность уменьшается в 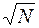раз. Т. о. случайные ошибки можно свести к нулю.

3. Промахи (грубые ошибки).

Самые точные приборы – стрелочные – по ним поверяют цифровые приборы, так как микросхемы могут ошибаться, могут стареть, могут получать дефекты, а в стрелочных используются дискретные элементы, их легко проверить, они более механически прочные.

Обычно у стрелочных приборов первая 1/3 и последняя 1/10 шкалы более неточные. Там результаты такие, что необходимо переключать прибор на другие пределы измерений. Такие значения нужно перемеривать, чтобы исключить ошибки. Поверку приборов проводит специальный отдел – ОГМЕТР.

Систематические и грубые ошибки можно устранить, а случайные свести к нулю путём увеличения числа измерений.

Свойства случайных ошибок:

1. Число отклонений в большую сторону равно числу отклонений в меньшую сторону.

2. Мелкие отклонения встречаются гораздо чаще, чем крупные (Гауссова кривая).

3. Величина самых крупных отклонений ограничена по размеру и её, как правило, называют предельной ошибкой.

4. Если просуммировать все случайные ошибки, то сумма равна нулю при большом числе измерений.

Регрессия – это когда массив данных описывается какой-то математической кривой. Когда строится зависимость, то все влияние всех несущественных параметров отбрасывается. Сложная зависимость сводится к более простой.

Аппроксимация – описание массива данных какой-либо известной формулой, которая ставит целью определение численных коэффициентов. Главное отличие аппроксимации от регрессии – то, что формула имеет какой-то физический смысл, по полученным коэффициентам можно судить о протекающих внутри чего-либо процессах.

Одним из самых эффективных методом регрессии считается сплайн-регрессия – между соседними точками строятся отрезки степенной функции (кубическая сплайн-регрессия, полиномы от 2-й до N-й степени, сплайн бывает параболическим).

Способы аппроксимации:

1. Графический способ – самый старый – строится график функции и его сравнивают с набором заранее построенных кривых, шаблонов. Недостаток этого метода – субъективность, поэтому все построения нужно проводить с использованием специальных компьютерных программ.

2. Способы приведения сложных кривых к линейному виду:

Пример: способ функциональных шкал (вместо у на шкале ставится ln(у) или а/у (а – коэффициент)). Функциональные шкалы используют для того, чтобы привести зависимость сложного вида к линейному виду.

3. Аналитические методы:

Пример: компьютерный подбор; в MathCAD – «Регрессия общего вида». Заключается в том, что в ЭВМ вводится массив исходных данных – координаты экспериментальных точек по х и по у, и аналитическая зависимость (формула с неизвестными коэффициентами). Компьютер путём подбора неизвестных коэффициентов пытается наиболее точно описать массив исходных данных.

Для того чтобы ускорить подбор коэффициентов строится пространство коэффициентов, показывается разница между реальным и вычисленным компьютером значениями. В зависимости от положения точек относительно экспериментальных значений определяется, в какую сторону изменять подбираемые коэффициенты для уменьшения погрешностей (существует много алгоритмов на ЭВМ).

Трудность аналитических методов.

Один и тот же набор экспериментальных точек может быть описан какой-либо кривой с различным набором коэффициентов, т. е. компьютеру всё равно, какие коэффициенты подобрать, а физического смысла нет, значит, начальную кривую надо задавать так, чтобы компьютер выдавал результат, имеющий физический смысл.