Бесконечно большие величины (функции). Ограниченные функции
Функция 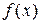 называется бесконечно большой величиной при
называется бесконечно большой величиной при 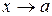 , если для любого положительного числа М можно подобрать такое
, если для любого положительного числа М можно подобрать такое 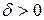 , что из неравенства
, что из неравенства 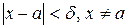 будет вытекать неравенство
будет вытекать неравенство 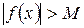 , т.е.
, т.е. 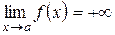 или
или 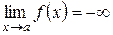 , или
, или 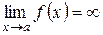 .
.
Бесконечно малые величины. Их свойства
Функция 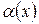 называется бесконечно малой величиной при
называется бесконечно малой величиной при 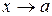 ; если каково бы ни было
; если каково бы ни было 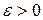 , можно подобрать такое
, можно подобрать такое 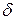 , зависящее от
, зависящее от 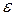 , что для всех
, что для всех 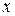 , удовлетворяющих неравенству
, удовлетворяющих неравенству 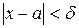 выполняется неравенство
выполняется неравенство 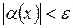 .
.
Основные теоремы бесконечно малых величин:
1) Если функция 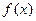 является бесконечно большой величиной, то
является бесконечно большой величиной, то 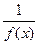 — бесконечно малая величина; если функция
— бесконечно малая величина; если функция 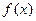 — бесконечно малая величина, то
— бесконечно малая величина, то 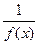 — бесконечно большая.
— бесконечно большая.
2) Сумма конечного числа бесконечно малых величин — величина бесконечно малая.
3) Произведение двух бесконечно малых величин есть величина бесконечно малая.
4) Произведение постоянной величины на бесконечно малую величину есть величина бесконечно малая.
5) Частное от деления бесконечно малой величины на величину, предел которой отличен от нуля, есть величина бесконечно малая.
Дата добавления: 2017-12-05; просмотров: 890;
