Точки разрыва и их классификация

Рассмотрим некоторую функцию 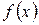, непрерывную в окрестности точки х₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х₀ является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел 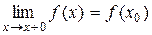, то функция называется непрерывной справа.

х₀

Рис. 5

Если односторонний предел 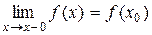, то функция называется непрерывной слева.

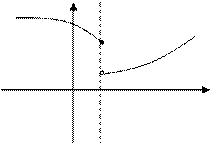х₀

Рис. 6

Точка х₀ называется точкой разрывафункции 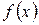, если 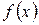не определена в точке х₀ или не является непрерывной в этой точке.

Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция 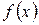имеет конечные пределы, cлева и справа, т.е. 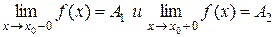. При этом:

а) если А₁=А₂, то точка х₀ называется точкой устранимого разрыва;

б) если А₁¹А₂, то точка называется точкой конечного разрыва.

Величину çА₁-А₂çназывают скачком функции в точке разрыва первого рода.

Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция 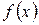не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Пример 20. Функция Дирихле[1] не является непрерывной в любой точке х₀.

Пример 21. Функция 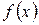= 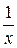имеет в точке х₀ = 0 точку разрыва 2 – го рода, т.к. .

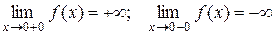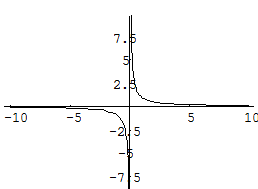
Рис. 6

Пример 22. =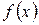

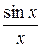
Функция не определена в точке х = 0, но имеет в ней конечный предел 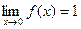, т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:

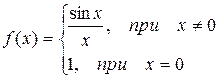
График этой функции:

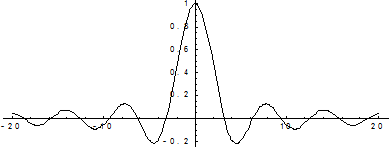
Рис. 7

Пример 23. =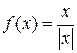

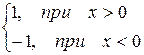
y

0 x

-1

Рис. 8

Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив 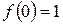, то функция будет непрерывна справа, если положить 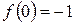, то функция будет непрерывной слева, если положить 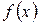равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях, тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.

Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.