Основные характеристики функции
Функция у = f(x), определённая на множестве D, называется чётной, если для 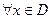 выполняется условие
выполняется условие 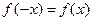 ; нечётной, если для
; нечётной, если для 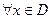 выполняется условие
выполняется условие 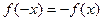 (график чётной функции симметричен относительно оси Оу, график нечётной относительно начала координат).
(график чётной функции симметричен относительно оси Оу, график нечётной относительно начала координат).
Пусть функция y = f(x) определена на множестве D и пусть D1 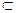 D.
D.
Если для любых значений 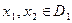 аргументов из неравенства
аргументов из неравенства 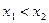 вытекает неравенство:
вытекает неравенство:
· 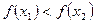 , то функция называется возрастающей на множестве D1;
, то функция называется возрастающей на множестве D1;
· 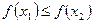 , то функция называется неубывающей на множестве D1;
, то функция называется неубывающей на множестве D1;
· 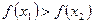 , то функция называется убывающей множестве D1;
, то функция называется убывающей множестве D1;
· 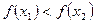 , то функция называется невозрастающей на множестве D1.
, то функция называется невозрастающей на множестве D1.
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D1 называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности.
Функцию у = f(x), определенную на множестве D, называют ограниченной на этом множестве, если существует такое число М > О, что
для всех х  D выполняется неравенство
D выполняется неравенство 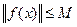 .
.
Функция у = f(x), определенная на множестве D, называется периодической на этом множестве, если существует такое число Т > 0, что при каждом х 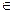 D значение (х + Т)
D значение (х + Т) 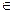 D и f(x + Т) = f(x). При этом число Т называется периодом функции.
D и f(x + Т) = f(x). При этом число Т называется периодом функции.
Замечание: обычно за основной период берут наименьшее положительное число Т, удовлетворяющее равенству f(x + Т) = f(x).
Обратная функция
Пусть задана функция у = f(x) с областью определения D и множеством значений Е. Если каждому значению у 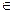 Е соответствует единственное значение х
Е соответствует единственное значение х 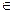 D, то определена функция х = φ (у) с областью определения Е и множеством D. Такая функция φ (у) называется обратной к функции f(x) .Про функции у = f(x) и х =φ (у) говорят, что они являются взаимно обратными.
D, то определена функция х = φ (у) с областью определения Е и множеством D. Такая функция φ (у) называется обратной к функции f(x) .Про функции у = f(x) и х =φ (у) говорят, что они являются взаимно обратными.
Замечание:
1) любая строго монотонная функция имеет обратную;
2) графики взаимообратных функций симметричны относительно биссектрисы первого и второго координатных углов.
Сложная функция
Пусть задана функция u = y (x), отображающая множество X в множество U, и пусть задана функция y= f(u) отображающая множество U в множество Y. Тогда последовательное отображение 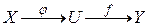 ставит в соответствии каждому элементу
ставит в соответствии каждому элементу 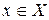 элемент
элемент 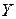 такой, что
такой, что 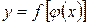 .
.
Дата добавления: 2017-12-05; просмотров: 2441;
