Показатели анализа рядов динамики

Для количественной оценки динамики проводят расчет таких показателей, как абсолютный прирост, темп роста, темп прироста, темп наращивания, абсолютное значение 1% прироста, средний уровень ряда динамики.

В основе расчета показателей ряда динамики лежит сравнительный анализ уровней ряда либо с постоянной, либо с переменной базой сравнения. При постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же показателем (уровнем), принятым за базу сравнения (у₀). В этом случае получают базисные показатели. При переменной базе сравнения каждый уровень ряда сравнивают с предыдущим уровнем (y_i-1) получают цепные показатели.

Таким образом, выделяют следующие аналитические показатели динамики:

1. Абсолютный прирост – это разность двух уровней ряда в исходных единицах измерения, которая характеризует абсолютное изменение уровня ряда за определенный промежуток времени:

- базисный: ;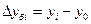

- цепной: .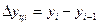

Абсолютный прирост может иметь отрицательное значение, если уровень изучаемого периода ниже уровня базисного периода или предшествующего.

Между цепными и базисным абсолютным приростом существует взаимосвязь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего уровня ряда динамики:

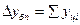
2. Темп роста – это отношение двух уровней ряда, выраженное в процентах. Он характеризует относительное изменение уровня динамического ряда за какой-либо период времени:

- базисный: ;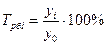

- цепной: .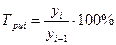

Если темп роста > 100%, то идет увеличение изучаемого уровня по сравнению с базисным или предыдущим показателем и наоборот.

Напомним, что средний темп роста определяется по формуле средней геометрической. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах ( 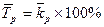), то средний темп роста определяется по формуле:

.

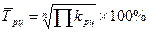Между базисным и цепными коэффициентами роста существует взаимосвязь – произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста последнего уровня ряда динамики:

.

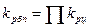3. Темп прироста – характеризует абсолютный прирост в относительных величинах:

- базисный: 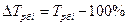или ;

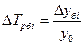- цепно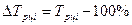й: или .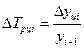

Если уровни ряда динамики сокращаются, то соответствующие показатели темпов прироста будут отрицательными, т.к. они характеризуют уменьшение ряда динамики в %.

Средний темп прироста определяется по формуле:

.

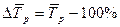4. Темп наращивания – показывает в экономике наращивание во времени экономического потенциала. Вычисляется делением цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения:

.

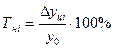5. Абсолютное значение одного процента прироста – применяется для сравнения абсолютного прироста и темпа прироста за одни и те же периоды времени, и показывает, какое абсолютное значение скрывается за относительным показателем – одним процентом прироста:

.

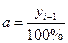6. Средний уровень ряда динамики – характеризует обобщенную величину абсолютных уровней.

Методы расчета среднего уровня интервального и моментного рядов динамики различны.

Для интервальных рядов динамики средний уровень за период времени определяется по формуле средней арифметической:

а) при равных интервалах применяется средняя арифметическая простая:

.

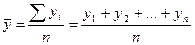б) при неравных интервалах применяется средняя арифметическая взвешенная:

.

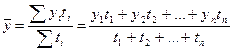Средний уровень моментного ряда динамики с равноотстоящими датами определяется по формуле средней хронологической простой:

.

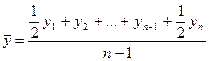Для моментных рядов с неравноотстоящими датами расчет среднего уровня ряда производится по формуле средней хронологической взвешенной:

.

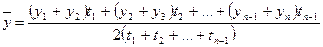Глава 7. Индексы

Виды индексов

В экономических исследованиях часто приходится сопоставлять не только отдельные признаки, но и сложные явления, состоящие из разнородных элементов, которые непосредственно суммироваться не могут. Изменение таких явлений изучают с помощью индексов.

Например, если необходимо дать характеристику изменения объема продукции промышленности. Отдельными элементами в этом случае выступают конкретные виды продукции в натурально-вещественной форме, имеющие разные единицы измерения (т, шт., л, м² и т.д.), поэтому их не возможно сразу суммировать, сначала нужно найти для них общую меру, например, стоимость продукции.

Индекс – это обобщающий показатель, который выражает соотношение величин какого-либо сложного явления во времени, в пространстве или дает сравнение фактических данных с любым эталоном (план, прогноз, норматив и т.д.).

С помощью индексов можно определить количественные изменения самых различных показателей развития социально-экономических процессов. Например, в экономике с помощью индексов можно объективно и точно показать изменения в росте или снижении производства, изменения в урожайности, себестоимости и цен выпускаемой продукции, численности работающих, производительности труда, заработной платы, изменение в цене акций на фондовых рынках и пр.

В статистике индексы классифицируются по ряду признаков:

а) по содержанию изучаемых величин:

1. Индексы количественных показателей – все индексируемые показатели этих индексов являются объемными, т.е. характеризуют общий, суммарный размер (объем) изучаемого явления и выражаются абсолютными величинами. К таким индексам относятся, например, индекс физического объема промышленной продукции, розничного товарооборота, национального дохода и т.д.

2. Индексы качественных показателей – характеризуют уровень явления в расчете на ту или иную единицу совокупности. Например, индекс себестоимости единицы продукции, индекс заработной платы, индекс производительности труда, индексы цен и т.д. Они измеряют не общий объем, а интенсивность, эффективность явления или процесса.

б) по степени охвата единиц совокупности:

1. Индивидуальные индексы характеризуют изменение отдельных элементов сложного явления, например, показывает изменение количества или цен по какому-либо одному виду продукции. Он определяется путем деления величины показателя за отчетный период на величину этого же показателя за базисный период.

2. Сводные (общие) индексы отражают изменение всех элементов сложного явления, например, изменение физического объема продукции, включающей разноименные товары.

3. Субиндексы (групповые) используются, если охватываются не все элементы сложного явления, а только их часть, например индексы физического объема продукции по отдельным отраслям промышленности, индексы цен по группам продовольственных и непродовольственных товаров.

в) по методам расчета общие индексы делят на:

1. Агрегатные индексы - сложные относительные показатели, которые характеризуют среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной в числителе и знаменателе (вес индекса).

2. Средние из индивидуальных - делятся на арифметические и гармонические и являются производными, т.е. они получаются в результате преобразования агрегатных и индивидуальных индексов.