Тангенциальная составляющая ускорения 17 страница
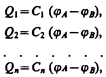
а заряд батареи конденсаторов
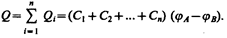
Полная емкость батареи
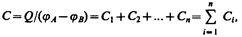
т. е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.
2. Последовательное соединение конденсаторов (рис. 145). У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи
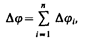
где для любого из рассматриваемых конденсаторов Dji = Q/Сi. С другой стороны,
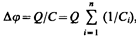

откуда
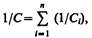
т. е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при .последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.
§ 95. Энергия системы зарядов, уединенного проводника и конденсатора. Энергия электростатического поля
1. Энергия системы неподвижных точечных зарядов. Электростатические силы взаимодействия консервативны (см. § 83); следовательно, система зарядов обладает потенциальной энергией. Найдем потенциальную энергию системы двух неподвижных точечных зарядов Q1и Q2, находящихся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (см. (84.2) и (84.5)):

где j12 и j21 — соответственно потенциалы, создаваемые зарядом Q2 в точке нахождения заряда Q1 и зарядом Q1 в точке нахождения заряда Q2. Согласно (84.5),
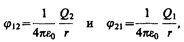
поэтому W1 = W2 = W и
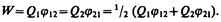
Добавляя к системе из двух зарядов последовательно зарядыQ3, Q4, ... , можно убедиться в том, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна
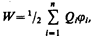 (95.1)
(95.1)
где ji — потенциал, создаваемый в той точке, где находится заряд Qi, всеми зарядами, кроме i-го.
2. Энергия заряженного уединенного проводника. Пусть имеется уединенный проводник, заряд, емкость и потенциал которого соответственно равны Q, С, j. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, затратив на это работу, равную
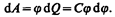

Чтобы зарядить тело от нулевого потенциала до j, необходимо совершить работу
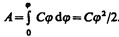 (95.2)
(95.2)
Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:
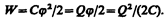 (95.3)
(95.3)
Формулу (95.3) можно получить и из того, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Полагая потенциал проводника равным j, из (95.1) найдем
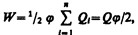
где 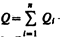 - заряд проводника.
- заряд проводника.
3. Энергия заряженного конденсатора. Как всякий заряженный проводник, конденсатор обладает энергией, которая в соответствии с формулой (95.3) равна
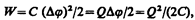 (95.4)
(95.4)
где Q — заряд конденсатора, С — его емкость, Dj — разность потенциалов между обкладками конденсатора.
Используя выражение (95.4), можно найтимеханическую (пондеромоторную) силу, с которой пластины конденсатора притягивают друг друга. Для этого предположим, что расстояние х между пластинами меняется, например, на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = — dW, откуда
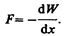 (95.5)
(95.5)
Подставив в (95.4) выражение (94.3), получим
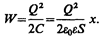 (95.6)
(95.6)
Производя дифференцирование при конкретном значении энергии (см. (95.5) и (95.6)), найдем искомую силу:
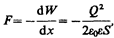
где знак минус указывает, что сила F является силой притяжения.
4. Энергия электростатического поля. Преобразуем формулу (95.4), выражающую энергию плоского конденсатора посредством зарядов и потенциалов, воспользовавшись выражением для емкости плоского конденсатора (C=e0eS/d) и разности потенциалов между его обкладками (Dj=Ed. Тогда
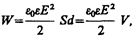 (95.7)
(95.7)
где V= Sd — объем конденсатора. Формула (95.7) показывает, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.
Объемная плотность энергии электростатического поля (энергия единицы объема)
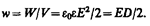 (95.8)
(95.8)
Выражение (95.8) справедливо только дляизотропного диэлектрика, для которого выполняется соотношение (88.2):Р ={e0Е.
Формулы (95.4) и (95.7) соответственно связывают энергию конденсатора с зарядом на его обкладках и с напряженностью поля. Возникает, естественно, вопрос о локализации электростатической энергии и что является ее носителем — заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика изучает постоянные во времени поля неподвижных зарядов, т. е. в ней поля и обусловившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на поставленные вопросы не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле.
Задачи
11.1. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 0,8 г/см3. Какова должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и керосине был один и тот же? Диэлектрическая проницаемость керосина e=2. [1,6 г/см3]
11.2. На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью s =1,5 нКл/см2 расположена круглая пластинка. Плоскость пластинки составляет с линиями напряженности угол a=45°. Определить поток вектора напряженности через эту пластинку, если ее радиус r=10 см. [1,88 кВ×м]
11.3. Кольцо радиусом r=10 см из тонкой проволоки равномерно заряжено с линейной плотностью t =10 нКл/м. Определить напряженность поля на оси, проходящей через центр кольца в точке А. удаленной на расстояние а =20 см от центра кольца. [1 кВ/м]
11.4. Шар радиусом R=10 см заряжен равномерно с объемной плотностью r =5 нКл/м3. Определить напряженность электростатического поля: 1) на расстоянии r1=2 см от центра шара; 2) на расстоянии r2=12 см от центра шара. Построить зависимость Е(r). [1) 3,77 В/м; 2) 13,1 В/м]
11.5. Электростатическое поле создается положительно заряженной бесконечной нитью с постоянной линейной плотностью t = 1 нКл/см. Какую скорость приобретет электрон, приблизившись под действием поля к нити вдоль линии напряженности с расстояния r1=2,5 см до r2=1,5 см? [18 Мм/с]
11.6. Электростатическое поле создается сферой радиусом R=4 см, равномерно заряженной с поверхностной плотностью s =1 нКл/м2. Определить разность потенциалов между двумя точками поля, лежащими на расстояниях r1=6 см и r2=10 см. [1,2 В]
11.7. Определить линейную плотность бесконечно длинной заряженной нити, если работа сил поля по перемещению заряда Q =1 нКл с расстояния r1 =10 см до r2 = 5 см в направлении, перпендикулярном нити, равна 0,1 мДж. [8 мкКл/м]
11.8. Пространство между обкладками плоского конденсатора заполнено парафином (e = 2). Расстояние между пластинами d=8,85 мм. Какую разность потенциалов необходимо подать на пластины, чтобы поверхностная плотность связанных зарядов на парафине составляла 0,05 нКл/см2? [500 В]
11.9. Свободные заряды равномерно распределены с объемной плотностью r =10 нКл/м3 по шару радиусом R = 5 см из однородного изотропного диэлектрика с диэлектрической проницаемостью e=6. Определить напряженности электростатического поля на расстояниях r1 = 2 см и r2 = 10 см от центра шара. [E1=1,25 В/м; E2=23,5 В/м]
11.10. Пространство между пластинами плоского конденсатора заполнено стеклом (e = 7). Расстояние между пластинами d=5 мм, разность потенциалов U=500 В. Определить энергию поляризованной стеклянной пластины, если ее площадь S = 50 см2. [6,64 мкДж]
11.11. Плоский воздушный конденсатор емкостью С=10 пФ заряжен до разности потенциалов U=1 кВ. После отключения конденсатора от источника напряжения расстояние между пластинами конденсатора было увеличено в два раза. Определить: 1) разность потенциалов на обкладках конденсатора после их раздвижения; 2) работу внешних сил по раздвижению пластин. [1) 2 кВ; 2) 5 мкДж]
11.12. Разность потенциалов между пластинами конденсатора U=200 В. Площадь каждой пластины S=100 см2, расстояние между пластинами d=1 мм, пространство между ними заполнено парафином (e = 2). Определить силу притяжения пластин друг к другу. [3,54 мН]
Глава 12Постоянный электрический ток
§ 96. Электрический ток, сила и плотность тока
В электродинамике — разделе учения об электричестве, в котором рассматриваются явления и процессы, обусловленные движением электрических зарядов или макроскопических заряженных тел, — важнейшим понятием является понятие электрического тока. Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием приложенного электрического поля Е свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля (рис. 146, а), т. е. в проводнике возникает электрический ток, называемый током проводимости. Если же упорядоченное движение электрических зарядов осуществляется перемещением в пространстве заряженного макроскопического тела (рис. 146, б), то возникает так называемый конвекционный ток.
Для возникновения и существования электрического тока необходимо, с одной стороны, наличие свободных носителей тока — заряженных частиц, способных перемещаться упорядоченно, а с другой — наличие электрического поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их упорядоченное движение. За направление тока условно принимают направление движения положительных зарядов.
Количественной мерой электрического тока служит сила тока I скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:
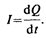
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока
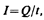
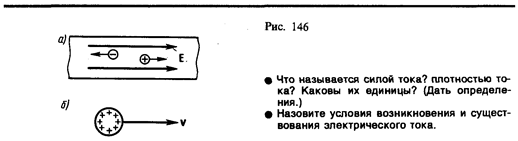
где Q — электрический заряд, проходящий за время t через поперечное сечение проводника. Единила силы тока — ампер (А).
Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока:
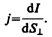
Выразим силу и плотность тока через скорость ávñ упорядоченного движения зарядов в проводнике. Если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е (что не обязательно для ионов), то за время dt через поперечное сечение S проводника переносится заряд dQ=ne ávñ S dt. Сила тока
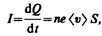
а плотность тока
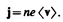 (96.1)
(96.1)
Плотность тока — вектор, ориентированный по направлению тока, т. е. направление вектора j совпадает с направлением упорядоченного движения положительных зарядов. Единица плотности тока — ампер на метр в квадрате (А/м2).
Сила тока сквозь произвольную поверхность S определяется как поток вектора j, т. е.
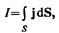 (96.2)
(96.2)
где dS=ndS (n — единичный вектор нормали к площадке dS, составляющей с вектором j угол a).
§ 97. Сторонние силы. Электродвижущая сила и напряжение
Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называютсяисточниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называютсясторонними.
Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п. Роль источника тока в электрической цепи, образно говоря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддерживается разность потенциалов и в цепи течет постоянный электрический ток.
Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называетсяэлектродвижущей силой (э.д.с.),действующей в цепи:
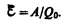 (97.1)
(97.1)
Эта работа производятся за счет энергии, затрачиваемой в источнике тока, поэтому величину 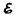 можно также называть электродвижущей силой источника тока, включенного в цепь. Часто, вместо того чтобы сказать: «в цепи действуют сторонние силы», говорят: «в цепи действует э.д.с.», т. е. термин «электродвижущая сила» употребляется как характеристика сторонних сил. Э.д.с., как и потенциал, выражается в вольтах (ср. (84.9) и (97.1)).
можно также называть электродвижущей силой источника тока, включенного в цепь. Часто, вместо того чтобы сказать: «в цепи действуют сторонние силы», говорят: «в цепи действует э.д.с.», т. е. термин «электродвижущая сила» употребляется как характеристика сторонних сил. Э.д.с., как и потенциал, выражается в вольтах (ср. (84.9) и (97.1)).
Сторонняя сила Fст, действующая на заряд Q0, может быть выражена как
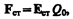
где Е — напряженность поля сторонних сил. Работа же сторонних сил по перемещению заряда Q0 на замкнутом участке цепи равна
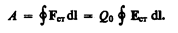 (97.2)
(97.2)
Разделив (97.2) на Q0, получим выражение для э. д. с., действующей в цепи:
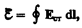
т. е. э.д.с., действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил. Э.д.с., действующая на участке 1—2, равна
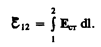 (97.3)
(97.3)
На заряд Q0 помимо сторонних сил действуют также силы электростатического поля Fe=Q0E. Таким образом, результирующая сила, действующая в цепи на заряд Q0, равна
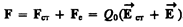
Работа, совершаемая результирующей силой над зарядом Q0 на участке 1—2, равна
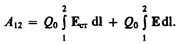
Используя выражения (97.3) и (84.8), можем записать
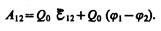 (97.4)
(97.4)
Для замкнутой цепи работа электростатических сил равна нулю (см. § 83), поэтому в данном случае 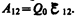
Напряжением U на участке 1—2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи. Таким образом, согласно (97.4),
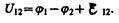
Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует Э.д.с., т. е. сторонние силы отсутствуют.
§ 98. Закон Ома. Сопротивление проводников
Немецкий физик Г. Ом (1787;—1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
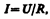 (98.1)
(98.1)
где R — электрическое сопротивление проводника. Уравнение (98.1) выражает закон Ома для участка цепи (не содержащего источника тока): сала тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Формула (98.1) позволяет установить единицу сопротивления — ом (Ом): 1 Ом — сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А. Величина
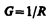
называется электрической проводимостью проводника. Единица проводимости — сименс (См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом.
Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:
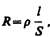 (98.2)
(98.2)
где r — коэффициент пропорциональности, характеризующий материал проводника и называемыйудельным электрическим сопротивлением. Единица удельного электрического сопротивления — ом×метр (Ом×м). Наименьшим удельным сопротивлением обладают серебро (1,6×10–8 Ом×м) и медь (1,7×10–8 Ом×м). На практике наряду с медными применяются алюминиевые провода. Хотя алюминий и имеет большее, чем медь, удельное сопротивление (2,6×10–8 Ом×м), но зато обладает меньшей плотностью по сравнению с медью.
Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (98.2) в закон Ома (98.1), получим
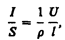 (98.3)
(98.3)
где величина, обратная удельному сопротивлению,
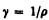
называетсяудельной электрической проводимостью вещества проводника. Ее единица — сименс на метр (См/м). Учитывая, что U/l = Е — напряженность электрического поля в проводнике, I/S = j — плотность тока, формулу (98.3) можно записать в виде
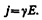 (98.4)
(98.4)

Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Поэтому формулу (98.4) можно записать в виде
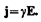 (98.5)
(98.5)
Выражение (98.5) — закон Ома в дифференциальном форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.
Опыт показывает, что в первом приближении изменение удельного сопротивления, а значит и сопротивления, с температурой описывается линейным законом:
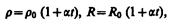
где r и r0, R и R0 — соответственно удельные сопротивления и сопротивления проводника при t и 0°С, a —температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 1/273 К–1. Следовательно, температурная зависимость сопротивления может быть представлена в виде
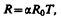
где Т — термодинамическая температура.
Качественный ход температурной зависимости сопротивления металла представлен на рис. 147 (кривая 1). Впоследствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах TK (0,14—20 К), называемыхкритическими, характерных для каждого вещества, скачкообразно уменьшается до нуля (кривая 2), т. е. металл становится абсолютным проводником. Впервые это явление, названное сверхпроводимостью, обнаружено в 1911 г. Г. Камерлинг-Оннесом для ртути. Явление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверхпроводящих материалов (в обмотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруднено из-за их низких критических температур. В настоящее время обнаружены и активно исследуются керамические материалы, обладающие сверхпроводимостью при температуре выше 100 К.
На зависимости электрического сопротивления металлов от температуры основано действиетермометров сопротивления, которые позволяют по градуированной взаимосвязи сопротивления от температуры измерять температуру с точностью до 0,003 К. Термометры сопротивления, в которых в качестве рабочего вещества используются полупроводники, изготовленные по специальной технологии, называютсятермисторами. Они позволяют измерять температуры с точностью до миллионных долей кельвин.

§ 99. Работа и мощность тока. Закон Джоуля — Ленца
Рассмотрим однородный проводник, к концам которого приложено напряжение U. За "время dt через сечение проводника переносится заряд dq=Idt. Так как ток представляет собой перемещение заряда dq под действием электрического поля, то, по формуле (84.6), работа тока
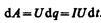 (99.1)
(99.1)
Если сопротивление проводника R, то, используя законОма (98.1), получим
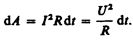 (99.2)
(99.2)
Из (99.1) и (99.2) следует, что мощность тока
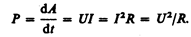 (99.3)
(99.3)
Если сила тока выражается в амперах, напряжение — в вольтах, сопротивление — в омах, то работа тока выражается в джоулях, а мощность — в ваттах. На практике применяются также внесистемные единицы работы тока: ватт-час (Вт×ч) и киловатт-час (кВт×ч). 1 Вт×ч — работа тока мощностью 1 Вт в течение 1 ч; 1 Вт×ч=3600 Bт×c=3,6×103 Дж; 1 кВт×ч=103 Вт×ч= 3,6×106 Дж.
Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии,
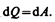 (99.4)
(99.4)
Таким образом, используя выражения (99.4), (99.1) и (99.2), получим
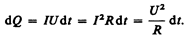 (99.5)
(99.5)
Выражение (99.5) представляет собойзакон Джоуля—Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем.*
* Э. X. Ленц (1804—1865) — русский физик.
Выделим в проводнике элементарный цилиндрический объем dV=dSdl (ось цилиндра совпадает с направлением тока), сопротивление которого 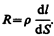 По закону Джоуля — Ленца, за время dt в этом объеме выделится теплота
По закону Джоуля — Ленца, за время dt в этом объеме выделится теплота
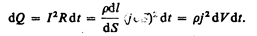
Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока. Она равна
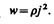 (99.6)
(99.6)
Используя дифференциальную форму законаОма (j=gЕ) и соотношение r=1/g, получим
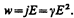 (99.7)
(99.7)
Формулы (99.6) и (99.7) являются обобщенным выражениемзакона Джоуля—Ленца в дифференциальной форме, пригодным для любого проводника.
Тепловое действие тока находит широкое применение в технике, которое началось с открытия в 1873 г. русским инженером А. Н. Лодыгиным (1847—1923) лампы накаливания. На нагревании проводников электрическим током основано действие электрических муфельных печей, электрической дуги (открыта русским инженером В. В. Петровым (1761—1834)), контактной электросварки, бытовых электронагревательных приборов и т. д.
§ 100. Закон Ома для неоднородного участка цепи
Мы рассматривали закон Ома (см. (98.1)) для однородного участка цепи, т. е. такого, в котором не девствует э.д.с. (не действуют сторонние силы). Теперь рассмотрим неоднородный участок цепи, где действующую э.д.с. на участке 1—2 обозначим через 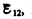 а приложенную на концах участка разность потенциалов — через j1 —j2.
а приложенную на концах участка разность потенциалов — через j1 —j2.
Дата добавления: 2017-04-20; просмотров: 539;
