Тангенциальная составляющая ускорения 16 страница

т. е. поверхностная плотность связанных зарядов s' равна поляризованности Р. Подставив в (88.3) выражения (88.4) и (88.2), получим

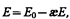
откуда напряженность результирующего поля внутри диэлектрика равна

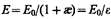(88.5)

Безразмерная величина

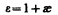(88.6)

называетсядиэлектрической проницаемостью среды. Сравнивая (88.5) и (88.6), видим, что e показывает, во сколько раз поле ослабляется диэлектриком, и характеризует количественно свойство диэлектрика поляризоваться в электрическом поле.

§ 88. Электрическое смещение. Теореме Гаусса для электростатического поля в диэлектрике

Напряженность электростатического поля, согласно (88.5), зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна e. Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачко­образное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризо­вать поле ещевектором электрического смещения, который для электрически изотроп­ной среды, по определению, равен

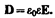(89.1)

Используя формулы (88.6) и (88.2), вектор электрического смещения можно выразить как

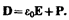(89.2)

Единица электрического смещения — кулон на метр в квадрате (Кл/м²).

Рассмотрим, с чем можно связать вектор электрического смещения. Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля, создаваемого системой свободных электрических зарядов, т. е. в диэлектрике на электростатическое поле свободных зарядов накладывается дополнительное поле свя­занных зарядов. Результирующее поле в диэлектрике описывается вектором напряжен­ности Е, и потому он зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, воз­никающие в диэлектрике, могут вызвать, однако, перераспределение свободных заря­дов, создающих поле. Поэтому вектор D характеризует электростатическое поле, создаваемое свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.

Аналогично, как и поле Е, поле D изображается с помощьюлиний электрического смещения, направление и густота которых определяются точно так же, как и для линий напряженности (см. §79).

Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.

Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверх­ность

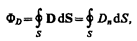
где D_n — проекция вектора D на нормаль n к площадке dS.

Теорема Гаусса дляэлектростатического поля в диэлектрике:

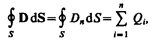(89.3)

т. е. поток вектора смещения электростатического поля в диэлектрике сквозь произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.

Для вакуума D_n = e₀E_n (e =1), тогда поток вектора напряженности Е сквозь произ­вольную замкнутую поверхность (ср. с (81.2)) равен

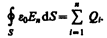
Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса (81.2) для поля Е в самом общем виде можно записать как

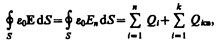
где 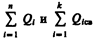— соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S. Однако эта формула неприемлема для описания поля Е в диэлектрике, так как она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения.

§ 90. Условия на границе раздела двух диэлектрических сред

Рассмотрим связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых e₁ и e₂) при отсут­ствии на границе свободных зарядов. Построим вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l, ориентировав его так, как показано на рис. 136. Согласно теореме (83.3) о циркуляции вектора Е,

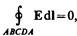
откуда

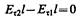
(знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы). Поэтому

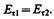(90.1)

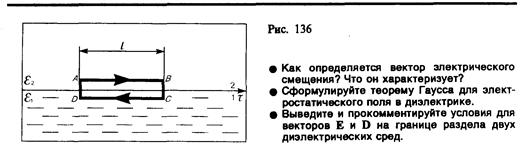
Заменив, согласно (89.1), проекции вектора Е проекциями вектора D, деленными на e₀e, получим

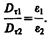(90.2)

На границе раздела двух диэлектриков (рис. 137) построим прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом диэлектрике, другое — во втором. Основания DS настолько малы, что в пределах каждого из них вектор D одинаков. Согласно теореме Гаусса (89.3),

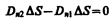
(нормалиnиn'к основаниям цилиндра направлены противоположно). Поэтому

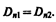(90.3)

Заменив, согласно (89.1), проекции вектора D проекциями вектора Е, умноженными на e₀e, получим

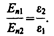(90.4)

Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е (Е_t) и нормальная составляющая вектора D (D_n) изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора Е (E_n) и тангенциальная составляющая вектора D (D_t) претерпевают скачок.

Из условий (90.1) — (90.4) для составляющих векторов Е и D следует, что линии этих векторов испытывают излом (преломляются). Найдем связь между углами a₁ и a₂ (на рис. 138 e₁>e₂). Согласно (90.1) и (90.4), Е_t2 = Е_t1 и e₂E_n2 = e₁E_n1. Разложим векторы E₁ и E₂ у границы раздела на тангенциальные и нормальные составляющие. Из рис. 138 следует, что

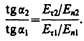
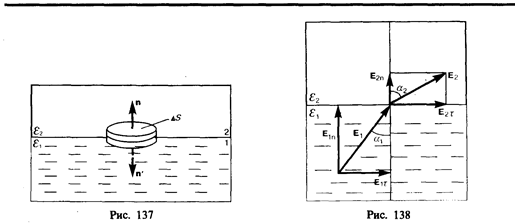
Учитывая записанные выше условия, получим закон преломления линий напряжен­ности Е (а значит, и линий смещения D)

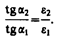
Эта формула показывает, что, входя в диэлектрик с большей диэлектрической проница­емостью, линии Е и D удаляются от нормали.

§ 91. Сегнетоэлектрики

Сегнетоэлектрики — диэлектрики, обладающие в определенном интервале температур спонтанной (самопроизвольной) поляризованностью, т. е. поляризованностью в отсут­ствие внешнего электрического поля. К сегнетоэлектрикам относятся, например, дета­льно изученные И. В. Курчатовым (1903—1960) и П. П. Кобеко (1897—1954) сегнетова соль NaKC₄H₄O₆ • 4Н₂О (от нее и получили свое название сегнетоэлектрики) и титанат бария ВаТiO₃.

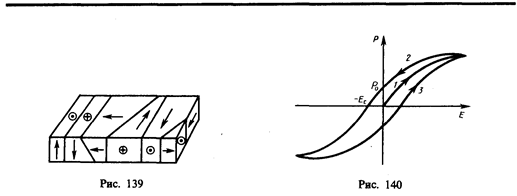
При отсутствии внешнего электрического поля сегнетоэлектрик представляет собой как бы мозаикуиздоменов — областей с различными направлениями поляризованности. Это схематически показано на примере титаната бария (рис. 139), где стрелки и знаки , Å указывают направление вектора Р. Так как в смежных доменах эти направления различны, то в целом дипольный момент диэлектрика равен нулю. При внесении сегнетоэлектрика во внешнее поле происходит переориентация дипольных моментов доменов по полю, а возникшее при этом суммарное электрическое поле доменов будет поддерживать их некоторую ориентацию и после прекращения действия внешнего поля. Поэтому сегнетоэлектрики имеют аномально большие значения ди­электрической проницаемости (для сегнетовой соли, например, e_max»10⁴).

Сегнетоэлектрические свойства сильно зависят от температуры. Для каждого сег­нетоэлектрика имеется определенная температура, выше которой его необычные свой­ства исчезают и он становится обычным диэлектриком. Эта температура называется точкой Кюри (в честь французского физика Пьера Кюри (1859—1906)). Как правило, сегнетоэлектрики имеют только одну точку Кюри; исключение составляют лишь сегнетова соль (—18 и +24°С) и изоморфные с нею соединения. В сегнетоэлектриках вблизи точки Кюри наблюдается также резкое возрастание теплоемкости вещества. Превращение сегнетоэлектриков в обычный диэлектрик, происходящее в точке Кюри, сопровождается фазовым переходом II рода (см. § 75).

Диэлектрическая проницаемость e (а следовательно, и диэлектрическая восприим­чивость {) сегнетоэлектриков зависит от напряженности Е поля в веществе, а для других диэлектриков эти величины являются характеристиками вещества.

Для сегнетоэлектриков формула (88.2) не соблюдается; для них связь между векторами поляризованности (Р) и напряженности (Е) нелинейная и зависит от значений Е в предшествующие моменты времени. В сегнетоэлектриках наблюдаетсяявление диэлектрического гистерезиса («запаздывания»). Как видно из рис. 140, с увеличением напряженности Е внешнего электрического поля поляризованность Р растет, достигая насыщения (кривая 1). Уменьшение Р с уменьшением Е происходит по кривой 2, и при Е=0 сегнетоэлектрик сохраняетостаточную поляризованность Р₀, т.е. сегнетоэлектрик остается поляризованным в отсутствие внешнего электрического поля. Чтобы унич­тожить остаточную поляризованность, надо приложить электрическое поле обратного направления (—E_с). Величина Е_c называетсякоэрцитивной силой (от лат. coercitio — удерживание). Если далее Е изменять, то Р изменяется по кривой 3петли гистерезиса.

Интенсивному изучению сегнетоэлектриков послужило открытие академиком Б. М. Вулом (1903—1985) аномальных диэлектрических свойств титаната бария. Титанат бария из-за его химической устойчивости и высокой механической прочности, а также из-за сохранения сегнетоэлектрических свойств в широком температурном интервале нашел большое научно-техническое применение (например, в качестве гене­ратора и приемника ультразвуковых воли). В настоящее время известно более сотни сегнетоэлектриков, не считая их твердых растворов. Сегнетоэлектрики широко применяются также в качестве материалов, обладающих большими значениями e (например, в конденсаторах).

Следует упомянуть еще опьезоэлектриках — кристаллических веществах, в которых при сжатии или растяжении в определенных направлениях возникает электрическая поляризация даже в отсутст­вие внешнего электрического поля(прямой пьезоэффект). Наблюдаетсяиобратный пьезоэффект — появление механической деформации под действием электрического поля. У некоторых пьезоэлектриков решетка положительных ионов в состоянии термодинамического равновесия смеще­на относительно решетки отрицательных ионов, в результате чего они оказываются поляризован­ными даже без внешнего электрического поля. Такие кристаллы называются пироэлектриками. Еще существуютэлектреты — диэлектрики, длительно сохраняющие поляризованное состояние после снятия внешнего электрического поля (электрические аналоги постоянных магнитов). Эти группы веществ находят широкое применение в технике и бытовых устройствах.

§ 92. Проводники в электростатическом поле

Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напряженность поля во всех точках внутри проводника равна нулю:

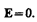
Отсутствие поля внутри проводника означает, согласно (85.2), что потенциал во всех точках внутри проводника постоянен (j = const), т. е. поверхность проводника в электростатическом поле является эквипотенциальной (см. § 85). Отсюда же следует, что вектор напряженности поля на внешней поверхности проводника направлен по нормали к каждой точке его поверхности. Если бы это было не так, то под действием касательной составляющей Е заряды начали бы по поверхности проводника переме­щаться, что, в свою очередь, противоречило бы равновесному распределению зарядов.

Если проводнику сообщить некоторый заряд Q, то нескомпенсированные заряды располагаются только на поверхности проводника. Это следует непосредственно из теоремы Гаусса (89.3), согласно которой заряд Q, находящийся внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равен

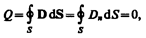
так как во всех точках внутри поверхности D=0.

Найдем взаимосвязь между напряженностью Е поля вблизи поверхности заряжен­ного проводника и поверхностной плотностью s зарядов на его поверхности. Для этого применим теорему Гаусса к бесконечно малому цилиндру с основаниями DS, пересека­ющему границу проводник — диэлектрик. Ось цилиндра ориентирована вдоль вектора Е (рис. 141). Поток вектора электрического смещения через внутреннюю часть цилинд­рической поверхности равен нулю, так как внутри проводника Е₁ (а следовательно, и D₁) равен нулю, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Со­гласно теореме Гаусса (89.3), этот поток (DDS) равен сумме зарядов (Q=sDS), охваты­ваемых поверхностью: DDS=sDS т.е.

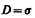(92.1)

или

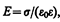(92.2)

где e — диэлектрическая проницаемость среды, окружающей проводник.

Таким образом, напряженность электростатического поля у поверхности провод­ника определяется поверхностной плотностью зарядов. Можно показать, что соот­ношение (92.2) задает напряженность электростатического поля вблизи поверхности проводника любой формы.

Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряды (электроны, ионы) будут перемещаться: положительные — по полю, отрицательные — против поля (рис. 142, а). На одном конце проводника будет скап­ливаться избыток положительного заряда, на другом — избыток отрицательного. Эти заряды называютсяиндуцированными. Процесс будет происходить до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряжен­ности вне проводника — перпендикулярными его поверхности (рис. 142, б). Таким образом, нейтральный проводник, внесенный в электростатическое поле, разрывает часть линий напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростати­ческой индукцией.

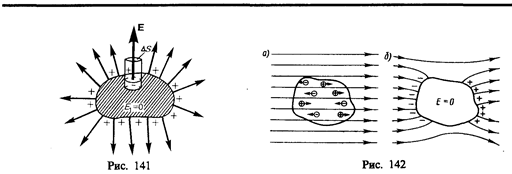
Из рис. 142, б следует, что индуцированные заряды появляются на проводнике вследствие смещения их под действием поля, т. е. s является поверхностной плот­ностью смещенных зарядов. По (92.1), электрическое смещение D вблизи проводника численно равно поверхностной плотности смещенных зарядов. Поэтому вектор D по­лучил название вектора электрического смещения.

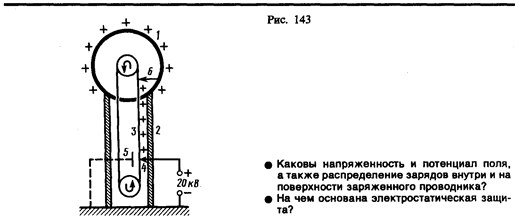
Таккак в состоянии равновесия внутри проводника заряды отсутствуют, то созда­ние внутри него полости не повлияет на конфигурацию расположения зарядов и тем самым на электростатическое поле. Следовательно, внутри полости поле будет отсут­ствовать. Если теперь этот проводник с полостью заземлить, то потенциал во всех точках полости будет нулевым, т. е. полость полностью изолирована от влияния внешних электростатических полей. На этом основанаэлектростатическая защи­та — экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Вместо сплошного проводника для защиты может быть использована густая металлическая сетка, которая, кстати, является эффективной при наличии не только постоянных, но и переменных электрических полей.

Свойство зарядов располагаться на внешней поверхности проводника используется для устройстваэлектростатических генераторов, предназначенных для накопления бо­льших зарядов и достижения разности потенциалов в несколько миллионов вольт. Электростатический генератор, изобретенный американским физиком Р. Ван-де-Граафом (1901—1967), состоит из шарообразного полого проводника 1 (рис. 143), укре­пленного на изоляторах 2. Движущаяся замкнутая лента 3 из прорезиненной ткани заряжается от источника напряжения с помощью системы остриев 4, соединенных с одним из полюсов источника, второй полюс которого заземлен. Заземленная пласти­на 5 усиливает стекание зарядов с остриев на ленту. Другая система остриев 6 снимает заряды с ленты и передает их полому шару, и они переходят на его внешнюю поверхность. Таким образом, сфере передается постепенно большой заряд и удается достичь разности потенциалов в несколько миллионов вольт. Электростатические генераторы применяются в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.

§ 93. Электрическая емкость уединенного проводника

Рассмотримуединенный проводник, т. е. проводник, который удален от других провод­ников, тел и зарядов. Его потенциал, согласно (84.5), прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряжен­ными, имеют различные потенциалы. Поэтому для уединенного проводника можно записать

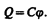
Величину

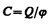(93.1)

называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изме­няет его потенциал на единицу.

Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала.

Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного провод­ника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл.

Согласно (84.5), потенциал уединенного шара радиуса R, находящегося в однород­ной среде с диэлектрической проницаемостью e, равен

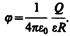
Используя формулу (93.1), получим, что емкость шара

(93.2)

Отсюда следует, что емкостью 1 Ф обладал бы уединенный шар, находящийся в ваку­уме и имеющий радиус R=C/(4pe₀)»9×10⁶км, что примерно в 1400 раз больше радиуса Земли (электроемкость Земли С»0,7 мФ). Следовательно, фарад — очень большая величина, поэтому на практике используются дольные единицы - миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ). Из формулы (93.2) вытекает также, что единица электрической постоянной e₀ — фарад на метр (Ф/м) (см. (78.3)).

§ 94. Конденсаторы

Как видно из § 93, для того чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, об­ладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили названиеконденсаторов.

Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду Q будут заряды противоположного знака. Эти заряды, естественно, ослабляют поле, создаваемое зарядом Q, т. е. понижают потенци­ал проводника, что приводит (см. (93.1)) к повышению его электроемкости.

Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми заря­дами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют (см. § 82): 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся наплоские, цилиндрические и сферические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начина­ются на одной обкладке и кончаются на другой, поэтому свободные заряды, воз­никающие на разных обкладках, являются равными по модулю разноименными заря­дами. Подемкостью конденсатора понимается физическая величина, равная отноше­нию заряда Q, накопленного в конденсаторе, к разности потенциалов (j₁ —j₂) между его обкладками:

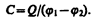(94.1)

Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать используя формулы (86.1) и (94.1). При наличии диэлектрика между обкладками разность потенциалов между ними, согласно (86.1),

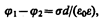(94.2)

где e — диэлектрическая проницаемость. Тогда из формулы (94.1), заменяя Q=sS, с учетом (94.2) получим выражение для емкости плоского конденсатора:

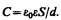(94.3)

Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиаль­ных цилиндров с радиусами r₁ и r₂ (r₂ > r₁), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками вычислим по формуле (86.3) для поля равномерно заряженного бесконечного цилиндра с линейной плотностью t =Q/l (l—длина об­кладок). При наличии диэлектрика между обкладками разность потенциалов

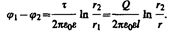(94.4)

Подставив (94.4) в (94.1), получим выражение для емкости цилиндрического конденсатора:

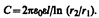(94.5)

Для определения емкости сферического конденсатора, состоящего из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу (86.2) для разности потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ (r₂ > r₁) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов

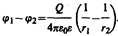(94.6)

Подставив (94.6) в (94.1), получим

Если d=r₂—r₁<<r₁, то r₂ » r₁ » r и C=4pe₀er²/d. Так как 4pr² —площадь сферической обкладки, то получаем формулу (94.3). Таким образом, при малой величине зазора по сравнению с радиусом сферы выражения для емкости сферического а плоского конденсаторов совпадают. Этот вывод справедлив и для цилиндрического конденсатора: при малом зазоре между цилиндрами по сравнению с их радиусами в формуле (94.5) ln (r₂/r₁) можно разложить в ряд, ограничиваясь только членом первого порядка. В результате опять приходим к формуле (94.3).

Из формул (94.3), (94.5) и (94.7) вытекает, что емкость конденсаторов любой формы прямо пропорциональна диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками. Поэтому применение в качестве прослойки сегнетоэлектриков значительно увеличивает емкость конденсаторов.

Конденсаторы характеризуются пробивным напряжением — разностью потенциа­лов между обкладками конденсатора, при которой происходит пробой — электричес­кий разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.

Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи, при этом используется их параллельное и последовательное соединения.

1. Параллельное соединение конденсаторов (рис. 144). У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна j_A – j_B. Если емкости отдельных конденсаторов С₁, С₂, ..., С_n, то, согласно (94.1), их заряды равны