Для запуска ракет в космическое пространство надо в зависимости от поставленных целей сообщать им определенные начальные скорости, называемые космическими.

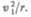Первом космической (или круговой) скоростью называют такую минимальную скорость, которую надо сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, т. е. превратиться в искусственный спутник Земли. На спутник, движущийся по круговой орбите радиусом г, действует сила тяготения Земли, сооб­щающая ему нормальное ускорение По второму закону Ньютона,

Если спутник движется вблизи поверхности Земли, тогда 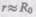(радиус Земли)

и 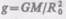(см. (25.6)), поэтому у поверхности Земли

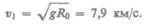
Первой космической скорости недостаточно для того, чтобы тело могло выйти из сферы земного притяжения. Необходимая для этого скорость называется второй космической. Второй космической (или параболической) скоростью называют ту наименьшую скорость, которую надо сообщить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спутник Солнца, т. е. чтобы его орбита в поле тяготения Земли стала параболической. Для того чтобы тело (при отсутствии со­противления среды) могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы его кинетическая энергия была равна работе, совер­шаемой против сил тяготения:

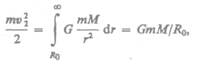
откуда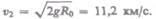

Третьей космической скоростью называют скорость, которую необходимо сооб- щить телу на Земле, чтобы оно покинуло пределы Солнечной системы, преодолев притяжение Солнца. Третья космическая скорость 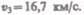Сообщение телам

таких больших начальных скоростей является сложной технической задачей. Ее первое теоретическое осмысление начато К. Э. Циолковским, им была выведена уже рассмот­ренная нами формула (10.3), позволяющая рассчитывать скорость ракет.

Впервые космические скорости были достигнуты в СССР: первая — при запуске первого искусственного спутника Земли в 1957 г., вторая — при запуске ракеты в 1959 г. После исторического полета Ю. А. Гагарина в 1961 г. начинается бурное развитие космонавтики.