Согласно формуле (12.2), работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому со знаком минус, т. е.
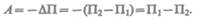
Из формулы (25.2) получаем
(25.3)
Так как в формулы входит только разность потенциальных энергий в двух состояниях, то для удобства принимают потенциальную энергию при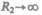 
равной нулю 
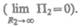Тогда (25.3) запишется в виде 
Так как первая точка была
выбрана произвольно, то 
Величина
является энергетической характеристикой поля тяготения и называется потенциалом. Потенциал пола тяготения 
— скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Таким образом, потенциал поля тяготения, создаваемого телом массой М, равен
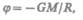(25.4)
где R — расстояние от этого тела до рассматриваемой точки.
Из формулы (25.4) вытекает, что геометрическое место точек с одинаковым потенциалом образует сферическую поверхность 
Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными.
Рассмотрим взаимосвязь между потенциалом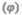 
поля тяготения и его напряженностью (g). Из выражений (25.1) и (25.4) следует, что элементарная работа dА, совершаемая силами поля при малом перемещении тела массой т, равна
С другой стороны, 
(dl — элементарное перемещение). Учитывая (24.1), полу-
чаем, что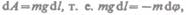 
или
|
|
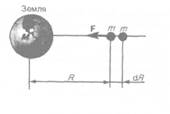
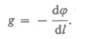
Величина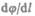 
характеризует изменение потенциала на единицу длины в направлении
Дата добавления: 2017-04-20; просмотров: 443;