Понятие об интерполяции и экстраполяции уровней динамического ряда

В некоторых случаях необходимо найти значения отсутствующих промежуточных уровней динамического ряда на основе известных его значений. В таких случаях можно использовать прием интерполяции, заключающийся в нахождении (восстановлении) недостающих уровней внутри динамического ряда.

Применение приема интерполяции должно быть основано на тщательном изучении закономерности изменения уровней динамического ряда. В соответствии с характером изменения уровней ряда и осуществляется интерполирование (восстановление) какого-нибудь неизвестного уровня. При правильно подобранном способе интерполяции значения расчетных уровней минимально отклоняются от фактических уровней динамического ряда.

Например, в сельскохозяйственной организации «Днепр» на 1 га посева зерновых культур было внесено в виде подкормки следующее количество минеральных удобрений (в пересчете на 100 % -ое содержание питательных веществ): в 2007 г. (У₀) – 128,5 кг; 2009 г. (У₂) – 135,1 кг; 2010 г. (У₃) – 137,7 кг. По этим данным необходимо определить примерный уровень внесения удобрений на 1 га посева в 2008 г. (У₁).

Приведенный динамический ряд имеет стабильный абсолютный прирост, поэтому интерполяцию уровня 2008 г. можно провести, например, по среднегодовому абсолютному приросту, воспользовавшись формулой (9.18). С этой целью определим среднегодовой абсолютный прирост внесения удобрений на га посева по формуле (9.7):

.

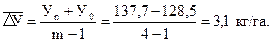На основании среднего абсолютного прироста найдем значение интерполируемого уровня У₁:

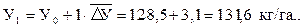
Таким образом, по нашим расчетам в 2008 г. было внесено на 1 га посева 131,6 кг/га (д.в.) минеральных удобрений.

Прием экстраполяции, в отличие от интерполяции, применяют при нахождении уровней , лежащих за пределами динамического ряда.

В основе экстраполяции значений уровня находится предположение о том, что характер динамики, выявленный за известный период, имел место в прошлом или сохранится в будущем. Прибегая к примеру экстраполяции уровней динамического ряда, можно воспользоваться разнообразными способами выравнивания динамических рядов: по прямой линии, показательной кривой, гиперболе, параболе второго порядка и т.д. Продолжая аналитическое выравнивание уровней, во многих случаях можно рассчитать значения неизвестных уровней за пределами динамического ряда.

Экстраполяцию уровня динамического ряда покажем на следующем примере. Заготовка сена в сельскохозяйственной организации «Днепр» за период с 2004 по 2009 г. изменялась следующим образом (тыс. т): 2004 г. – 3,7; 2009 г. – 13,0. Необходимо установить, какой объем заготовок сена мог быть достигнут в 2010 г. (У₇). Для этого динамического ряда характерны относительные стабильные темпы роста динамики. Поэтому при экстраполяции уровня 2010 года за основу можно принять среднегодовой темп роста объема заготовки сена. Значение искомого уровня рассчитаем по формуле (9.19). Прежде всего найдем среднегодовой коэффициент роста уровней в приведенном динамическом ряду по формуле (9.19):

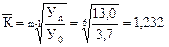раза (123,2 %).

Теперь определим значение экстраполируемого уровня (У₇):

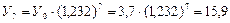тыс. ц.

Таким образом, экстраполируемый объем заготовки сена в 2010 г. может составить 15,9 тыс.т.

Использование интерполяции и экстраполяции при расчете уровней динамического ряда носит ограниченный характер, так как в развитии многих явлений может быть большие отклонения, а расчетные показатели, полученные на основе выравнивания рядов динамики, имеют обычно приближенные значения. Комбинирование различных статистических методов в сочетании с разнообразными приемами экстраполяции может служить основой при разработке прогноза многих важнейших экономических показателей развития явлений.