Нормальные и касательные напряжения по наклонной площадке
Рассмотрим элементарный тетраэдр ABCD, три грани которого параллельны координатным плоскостям, а нормаль N к четвертой грани составляет с координатными осями углы, косинусы которых равны l, т и п (рис. 6). Будем считать заданными составляющие нормальные и касательные напряжения, действующие по площадкам, лежащим в координатных плоскостях, и определим напряжения на площадке BCD. Выберем новую систему прямоугольных осей координат х1 , y1 иz1, так чтобы ось х1 совпадала с нормалью N , а оси у1 и z1 лежали в плоскости площадки BCD. Каждая из этих осей будет иметь в системе осей x, y, z свои направляющие косинусы, указанные в табл. 1.
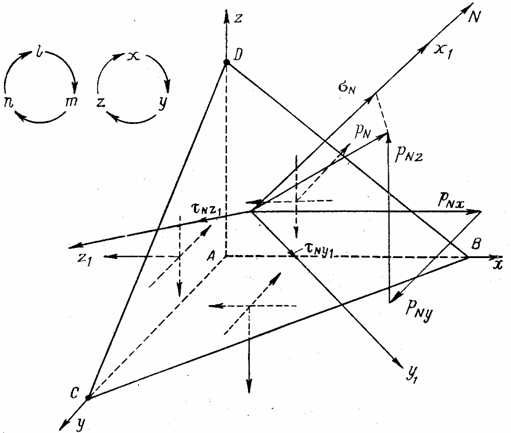
Рис. 6
Таблица 1
| Оси | x | y | z |
| x1 | l1 | m1 | n1 |
| y1 | l2 | m2 | n2 |
| z1 | l3 | m3 | n3 |
Полное напряжение рN, действующее по площадке BCD, разложим на составляющие рNx , pNy и pNz . Нормальное напряжение действующее по площадке BCD, можно рассматривать как проекцию на ось N (или х1) полного напряжения pN , действующего по площадке BCD, а полное напряжение рN - как равнодействующую трех его проекций. Так как проекция равнодействующей равна сумме проекций составляющих, то
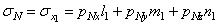 .
.
Подставив выражения (1.4) и произведя необходимые сокращения, запишем
sN = sx l2 + sy m2 + sz n2 + 2txy lm + 2tyz mn + 2tzx nl. (1.6)
Спроектировав составляющие рNx , pNy и pNz на ось у1 (рис. 6), получим
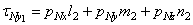 ,
,
а заменив их выражениями (1.4) и приведя подобные члены, -
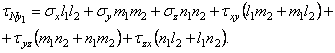 (1.7,а)
(1.7,а)
Аналогично из суммы проекций на ось z1 найдем выражение для третьего составляющего касательного напряжения
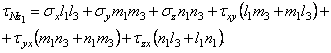 (1.7,б)
(1.7,б)
С помощью формул (1.6) и (1.7) можно преобразовать составляющие тензора напряжений при переходе от одной системы координат х, у, z к новой системе координат х1, у1, z1.
Для записи (1.6), (1.7) и ряда других формул теории упругости можно установить последовательность чередования индексов у составляющих напряжений и чередования направляющих косинусов, показанную схематически на рис. 6.
Дата добавления: 2015-10-26; просмотров: 1222;
