Анализ ферм на геометрическую неизменяемость

Ферма должна быть геометрически неизменяемой системой. В этом необходимо убедиться перед расчетом. Проверка необходимого условия геометрической неизменяемости может быть проведена с помощью формулы (3.1), приведенной выше. Однако эта формула, определяющая степень свободы в применении к фермам, неудобна ввиду большого количества стержней, принимаемых за диски, и затруднительности подсчета простых шарниров.

Проверку выполнения необходимого условия геометрической неизменяемости ферм болееудобно производить с помощью формулы

С_Ф + С_ОП = 2У, (3.23)

где С_Ф - количество стержней фермы; С_ОП - количество опорных стержней;

У - количество узлов фермы независимо от числа стержней, сходящихся в узле.

Если С_Ф + С_ОП = 2У или С_Ф = 2У - 3 (эту формулу применяют при анализе фермы, лишенной связи с землей), то система геометрически неизменяема и статически определима (рис. 3.33 б).

Если С_Ф + С_ОП < 2У или С_Ф < 2У - 3, то система изменяема (рис. 3.33 а).

Если С_Ф + С_ОП > 2У или С_Ф < 2У - 3, то система геометрически неизменяема, но статически неопределима (рис.3.33 в).

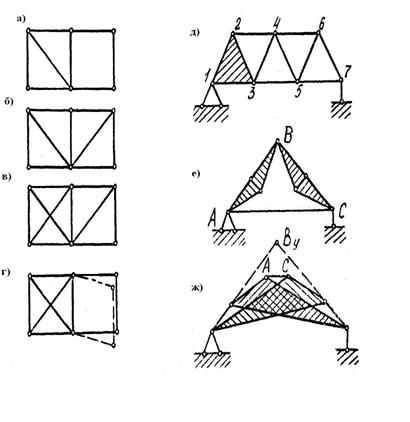
Рис. 3.33. Примеры ферм для анализа геометрической неизменяемости:

а - геометрически изменяемая система; б - геометрически неизменяемая система; в - геометрически неизменяемая статически неопределимая система; г - геометрически изменяемая система; д - геометрически неизменяемая треугольная ферма; е - геометрически неизменяемая система с дисками АВ и ВС; ж - геометрически неизменяемая система имеет два диска (заштрихованы), общий шарнир В_У (условный) и стержень АС

Ферма должна быть неизменяемой системой. Изменяемая система не может применяться как ферма.

Следует понимать, что формула (3.23) дает возможность проверить, существует ли необходимое соотношение между элементами (С_Ф, С_ОП,У), дающее возможность конструировать неизменяемую систему. Это необходимое соотношение элементов и записано в виде уравнения (3.23). Но выполнение этого условия отнюдь не гарантирует, что сконструированная система обязательно является геометрически неизменяемой. Конструкция, показанная на рис. 3.33 г удовлетворяет условию С_Ф = 2У - 3, но не является фермой, так как она геометрически изменяема.

Следовательно, наличие элементов в системе в соотношении (3.23) является необходимым, но недостаточным условием геометрической неизменяемости системы.

Для того, чтобы окончательно убедиться в том, что сконструированная система неизменяема, необходимо провести анализ ее структуры. Анализ структуры проводят без связи системы с землей, если число опорных стержней равно трем. Если число опорных стержней равно четырем (и более) анализ проводят в связи системы с землей, считая последнюю диском. Напоминаем, что к анализу структуры можно приступить, если выполняется условие (3.23).

Рассмотрим два основных способа анализа структуры.

Первый способ применяют, если в основу фермы положен стержневой треугольник, а ферма образована последовательным присоединением к нему (треугольнику) узлов, каждого двумя стержнями. Образованная таким образом ферма (она называется фермой простейшего образования) является неизменяемой системой. При анализе необходимо идти обратным путем, разбирая ферму последовательным отбрасыванием узлов, присоединенных двумя стержнями, начиная с крайнего узла. Если в конце такой операции останется треугольник (или вообще любой диск), то делаем заключение, что ферма в целом геометрически неизменяема.

Например, ферма, показанная на рис. 3.33, д удовлетворяет условию (3.23).

Число стержней фермы С_Ф = 11, число опорных стержней С_ОП = 3, число узлов У = 7.

11 + 3 = 2 · 7.

Лишаем ферму связи с землей. Затем последовательно отбрасываем узлу 7,6,5,4. В результате остается стрежневой треугольник 1-2-3. На основании этого делаем заключение, что ферма статически определима и геометрически неизменяема.

Для фермы, приведенной на рис. 3.33 е, ж, условие (3.23) также удовлетворяется. Но рассмотренный способ анализа структуры к этой ферме применить не удается. Лишив ферму связи с землей (С_ОП = 0), мы видим, что у фермы нет ни одного узла, присоединенного двумя стержнями.

Анализ этой фермы (и подобных) необходимо проводить, применяя второй -способ. Суть его в следующем. Необходимо выделить части фермы, которые являются дисками. На рис. 3.33 е, ж они заштрихованы. Эти два диска соединены между собой шарниром В (условным) и стержнем АС, что достаточно для образования единой неизменяемой системы.

Делаем заключение: ферма в целом статически определима и геометрически неизменяема. Напомним, что для образования единой неизменяемой системы два диска должны быть соединены шарниром и стержнем или тремя стержнями. Причем эти три соединяющих стержня не должны пересекаться в одной точке. В этом случае система будет мгновенно изменяемой, что недопустимо. Три диска должны быть соединены тремя шарнирами или эквивалентным количеством стержней. Шарниры не должны располагаться на одной прямой, а соединяющие стержни - пересекаться в одной точке. В этих случаях системы также будут мгновенно изменяемыми.

Предлагается провести анализ ферм, показанных на рис. 3.34, самостоятельно.

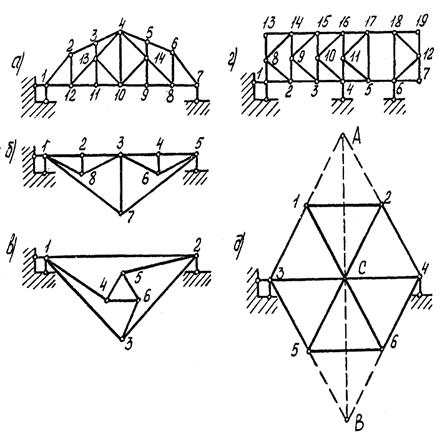
Рис. 3.34. Примеры ферм для самостоятельного анализа