Построение линий влияния

Изучение способа аналитического расчета многопролетных статически определимых балок на неподвижную нагрузку показало, что основной задачей расчета является определение расчетных уси­лий M_max и Q_max. Эта задача решается путем построения эпюр М и Q от заданной неподвижной нагрузки.

В то же время большое число инженерных сооружений, несущей частью которых являются сварные металлические конструкции, в том числе и балки, работают при воздействии подвижных нагрузок. Это железнодорожные и автодорожные мосты, подкрановые бал­ки и мосты кранов и др. Определить в этом случае расчетные усилия с помощью эпюр М и Q практически невозможно. Поэтому расчет на подвижную нагрузку производится иным способом.

Расчет сооружения на подвижную нагрузку в значительной степени об­легчается возможностью применения принципа независимости действия сил, сущность которого заключается в том, что внутренние усилия, напря­жения и деформации, вызванные воздействием на сооружение различных нагрузок, можно суммировать.

Если, например, на сооружение одновременно действуют две группы сил, то возникающее при этом усилие в любом элементе сооружения будет равно сумме усилий, возникающих в нем при действии каждой группы сил в отдельности. Исследование действия на сооружение подвижной нагрузки нач­нем с рассмотрения наиболее простого случая, когда по сооружению движется только один вертикальный груз Р, равный единице (рис. 3.14). Исследуем, как меняется тот или иной фактор (например, опорная реакция, изгибающий момент в определенном сечении балки, прогиб балки в данной точке и т. п.) при перемещении груза Р = 1 по сооружению. Установленный при этом закон изменения изучаемого фактора в зависи­мости от положения перемещающегося груза Р = 1 будем изображать графически.

График, изображающий закон изменения какого-либо силового фактора (напри­мер, изгибающего момента в сечении) при передвижении по сооружению силы Р = 1, называется линией влияния этого фактора.

Понятие о линиях влияния. Очевидно, что величина любого усилия в элементах несущих конструкций зависит от положения внеш­ней подвижной нагрузки. Например, в однопролетной балке на двух опорах (рис, 3.14) величина опорной реакции R_A будет тем больше, чем ближе к опоре находится подвижный груз Р, и наоборот, R_A тем меньше, чем дальше от опоры А находится подвижный груз Р.

График, выражающий закон изменения усилий (опорных реакций, изгибающих моментов, поперечных сил в заданном сечении балки) в зависимости от положения на балке подвижного единичного груза Р = 1, называется линией влияния.

Рассмотрим порядок построения линий влияния опорных реакций однопролетных балок.

Однопролетная статически определимая балка АВ (рис. 3.14 а). Нагрузка на балку - подвижный единичный груз Р = 1. Определим величину опорной реакции R_A в зависимости от положения Р = 1 (в текущих координатах ).

∑М_В = 0; R_A · L - P ( L - X) = 0; R_A = (L - X)/L. (3.12)

Уравнение (3.12) это уравнение прямой линии. Определим ее положение в координатах X – Y.

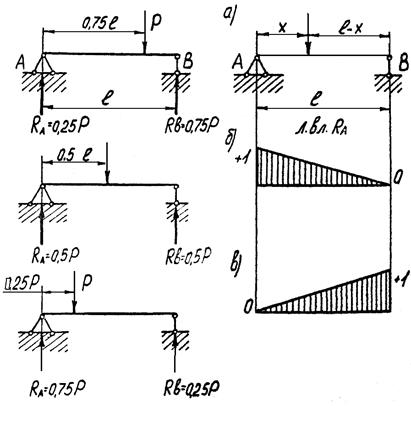
При Х = 0,75L R_A = 0,25P, при Х = 0,5L R_A = 0,5P., При Х =0,25L R_A = 0,75Р , что и представлено в левой части рис. 3.14.

.

Рис. 3.14. Анализ изменения опорных реакций R_A и R_B в зависимости от положения единичного груза Р = 1 c построением графиков линий влияния опорных реакций R_A (б) и R_B (в) в зависимости от положения единичного груза при Р = 1

Отложим на левой опоре (Х = 0) ординату, равную + 1, в произволь­ном масштабе, на правой опоре (Х = L) - ординату, равную нулю. Найденные две точки определяют положение прямой, которая и является линией влияния опорной реакции R_A (рис. 3.14 б). С помощью полученного графика можно определить величину опорной реакции при любом положении груза Р = 1. Для этого достаточно измерить ординату под грузом. Эта ордината (в принятом масштабе) будет равна опорной реакции R_A при данном положении Р = 1. Линия влияния изображена на рис 3.14 в.

Рассмотрим на примере использование линии влияния для практических целей. Однопролетная балка АВ (рис. 3.15) нагружена тремя неподвижными сосредоточенными силами.

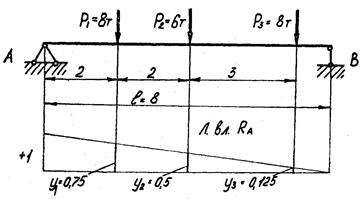
Рис. 3.15. Использование линии влияния для определения опорной реакции R_A

С помощью линии влияния определим величину R_A от действия данной нагрузки. Для этого воспользуемся одним из следствий принципа независи­мости действия сил: результаты воздействия на сооружение различных нагрузок можно суммировать. На основании этого

R_A = P₁· y₁ + P₂ · y₂ + P₃ · y₃ = 8 · 0,75 + 6 · 0,5 + 8 · 0,125 = 10 т (3.13) Рассмотрим порядок построения линии влияния изгибающего момента в произвольно выбранном сечении балки.

Статически определимая балка на двух oпорах АВ (рис. 3.16 а). Найдем изгибающий момент в сечении I - I, которое находится на расстоянии а от левой опоры. Если подвижный единичный груз Р = 1 находится справа от сечения (рис. 3.16 а), то изгибающий момент в сечении равен

М₁ = R_A · а = а · (L - X)/ L. (3.14)

График уравнения (3.14) также прямая, которая и является линиейвлияния изгибающего момента в сечении I - I (рис. 3.16 в). Но это не вся линия влияния, а только ее правая ветвь. Она действительна от опоры В до сечения, так как уравнение (3.14) состав­лено при условии, что груз Р=1 находится на этой (правой) части балки. Переместим груз Р = 1 на часть балки слеваот сечения I - I . Тогда момент в сечении I - I равен

М₁ = R_B · b. (3.15)

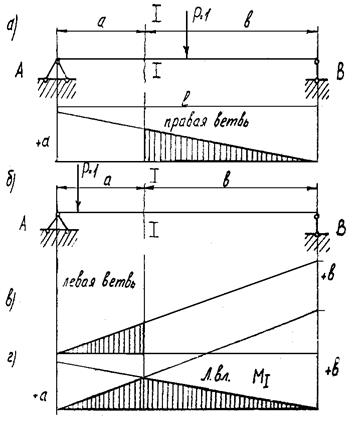
Рис 3.16. Построение линии влияния изгибающего момента в сечении I - I

Строим график уравнения (3.15). На правой опоре откладываем орди­нату, равную отрезку, в. Прямая, соединяющая точки с ординатой в на правой опоре и с ординатой, равной нулю, налевой опоре, является линией влияния момента в сечении I - I. Но, как теперь понятно, это также не вся линия влияния, а ее левая ветвь (рис. 3.16 в). Объединив обе ветви, получим полную линию влияния из­гибающего момента в сечении I - I (рис. 3.16 г). Размерность ординат линии влияния изгибающего момента - метры (сантиметры).

Необходимо обратить внимание на следующее обстоятельство. Линия влияния М₁ по очертанию подобна эпюре изгибающих моментов от действия сосредоточенной силы. Но это сходство толь­ко внешнее. Между эпюрой изгибающих моментов и линией влияния изгибающего момента имеется принципиальная разница. Если эпюра моментов - это график распределения моментов во всех сечениях балки от неподвижной определенной нагрузки, то линия влияния момента - это график величин моментов в одном определенном сечении балки в зависимости от положения подвижного единичного груза Р = 1.

Рассмотрим построение линии влияния поперечной силы.

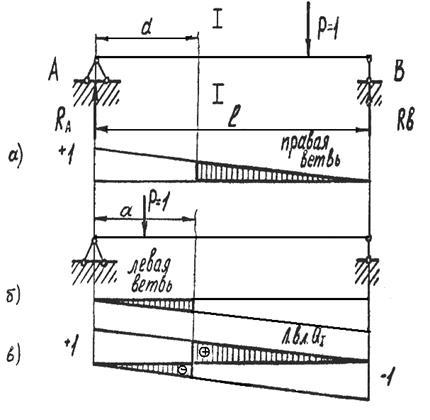
Рис. 3.17. Построение линии влияния поперечной силы Q

Статически определимая балка на двух опорах АВ (рис. 3.17). Построим линию влияний поперечной силы Q _I для сечения I - I, находящегося на расстоянии a левой опоры. Если подвиж­ный единичный груз Р = 1 находится справа от сечения I - I, то величина поперечной силы в сечении равна

Q _I = + R_A. (3.16)

Напомним, что правило определения знаков поперечных сил в сечении рассмотрено выше (раздел 3.3.3, рис. 3.13).

Из уравнения (3.16) следует, что поперечная сила Q _I и опорная реакция R_A в зависимости от положения подвижного единично­го груза Р = 1 изменяются по одному и тому же закону. Следовательно, линия влияния R_A будет также правой ветвью линии влияния Q _I (рис. 3.17 а).

Переместим груз Р =1 на часть балки слева от сечения I - I. Тогда

Q _I = - R_В. (3.17)

Из уравнения (2.17) следует, что линия влияния R_В (с обратным знаком) будет также левой ветвью линии влиянияQ _I (рис. 3.17 б). Объединив обе ветви, получим полную линию влияния поперечной силы в сечении I - I (л.вл. Q _I) (рис 3.17 в).

Рассмотрим построение линий влияния для однопролетных балок с консолями (рис. 3.18).

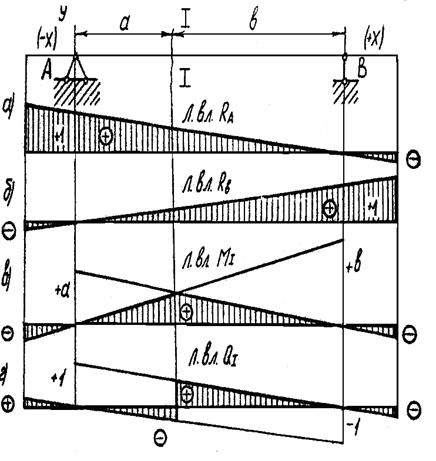
Рис 3.18. Балка АВ с линиями влияния R_A,_, R_B, M и Q в сечении I – I между опорами

Построение линий влияния опорных реакций, изгибающего момента и поперечной силы для сечений, находящихся в пределах основного пролета АВ, производится по тем же правилам, что и для балки без консолей.

Величина опорной реакции R_A в текущих координатах опре­деляется по формуле (3.12), приведенной выше.

R_A = (L - X)/L,

Формула (3.12) справедлива при всех положениях груза Р = 1, включая консоли (рис. 3.18 а). Построение линии влияний опорной реакции R_A : соединяем прямой две точки - первую с ординатой, равной + 1, на левойопоре, и вторую с ординатой, равной нулю, на правой опоре. Затем продолжаем прямую до концов консолей. В пределах правойконсоли ординаты отрицательные. Это означает, что R_A направлена вниз,когда груз Р = 1 находится в пределах этой консоли.

Линию влияния момента в сечении I-I построим как для обычной балки, но левую и правую ветви продолжим до концов консолей (рис. 3.18 в). В пределах консолей ординаты линии влияния отрицатель­ны. Это означает, что момент всечении I - I отрицателен, когда груз Р = 1 находится на консолях.

При построении линии влияния поперечной силы в сечении I - I правую и левую ветви необходимо продолжить до конца консолей (рис. 3.18, г).

Построение линий влияния изгибающего момента и поперечной силы для сечений, находящихся на консолях, производится по иным правилам (рис. 3.19).

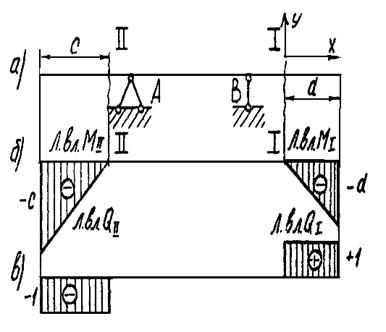
Рис. 3.19. Линии влияния изгибающих моментов М₁ и М_1I и поперечных сил Q _I и Q _II для сечений I – I и II – II на консолях балки

Линия влияния изгибающего момента в сечении I - I будет только в пределах от сечения I - I до конца консоли. Представляется очевидным, что когда груз Р = 1 находится слева от сечения I - I, сечение не работает, в нем нет изгибающего момента (и поперечной силы).

Поэтому ординаты линии влияния М₁ слева от сечения I - I равны нулю. Величина изгибающего момента в сечении I - I в текущих координатах (рис. 3.19 а), равна

М₁ = -Р · Х = -Х

Когда груз Р = 1 находится над сечением (Х = 0), М₁ = 0, когда груз находится на краю консоли (Х = d), М₁ = -d. Линия влияния М₁ и М_1I приведены на рис. 2.19 б; линии влияния Q _I и Q _II - на рис. 3.19 в. (Знаки ординат линий влияния изгибающих моментов М₁ и М_1I и поперечных сил Q _I и Q _II определены всоответствии со схемами, показанными на рис. 3.13).

Рассмотрим построение линий влияния для многопролетных статически определимых балок.

Построение линий влияния для многопролетных статически определимых балок базируется на тех же закономерностях, которые используются при исследовании однопролетных балок.

Рассмотрим балку А-Н (рис. 3.20 а). Балка статически определима и геометрически неизменяема. Составим схему взаимодействия (рис. 3.20 б), которая помогает определить основные и вспомогательные элементы.

При построении линий влияния следует руководствоваться следующими правилами:

а) линии влияния для второстепенного элемента не отличаются по правилам построения от линий влияния для обычной однопролетной балки и не выходят за пределы элемента;

б) при построении линий влияния для основного элемента сначала строим ее, не обращая внимания на второстепенные элементы, как для обычной однопролетной балки, а затем учитываем их воз­действие (второстепенных элементов).

Рассмотрим построение линий влияния на примере для балки А-Н (рис. 3.20 а).

Линии влияния опорных реакций R_A и R_В (рис. 3.20 в, г), строим сначала в пределах основного элемента ABC, как для обычной балки с консолями. Когда груз Р = 1 перейдет на второстепенный элемент СД, его воздействие на величину опорных реакций R_A и R_В начнет уменьшаться и станет равным нулю при положении груза в точке Д. Соответственно равным нулю при этом положении груза Р = 1 станут и величины опорных реакций R_A и R_В. Правее шарнира Д ординаты линий влияния R_A и R_В равны нулю, так как при положении груза Р = 1 правее шарнира Д он не оказывает никакого воздействия на эти опорные реакции.

Линии влияния М_1II и Q_1II для сечения III - III, находящегося на второстепенной балке СД, не отличаются от линий влияния для обычной однопролетной балки (рис. 3.20 д).

Линии влияния М₁ и Q₁ для сечения I - I, находящегося впределах основного пролета основного элемента ABC, строим, придерживаясь правил, примененных при построении линий влияния R_A и R_В (рис. 3.20 е).

Линии влияния М_1I и Q_1I для сечения II - II, находящегося на консольной части основного элемента ABC, строим сначала как для обычной балки, затем учитываем воздействие второстепенного элемента СД. Когда груз Р = 1 достигнет шарнира Д, его воздействие через элемент СД на величину М_1I и Q_1I прекратится (рис.3.20 ж).

Линии влияния R_Е, М_1V и Q_1V подобны по построению линиям влияния соответственно R_A, М₁ и Q₁, так как элемент ДЕFG также является основным. Только на величину R_Е, М_1V и Q_1V помимо второстепенного элемента СД оказывает воздействие второй второстепенный элемент GH (рис. 3.20 з, и, к).

Линия влияния М_V подобна по построению линии влияния М_1I, а линия влияния М_1V - соответственно линии влияния М_1II (рис. 3.20 л, м).

Правильность построения линий влияния можно проверить статическим способом. Для этого, располагая груз Р = 1 в произволь­но выбранных сечениях на балке, необходимо составить и решить соответствующие уравнения статики (по методике, рассмотренной в разделе 3.3.3).

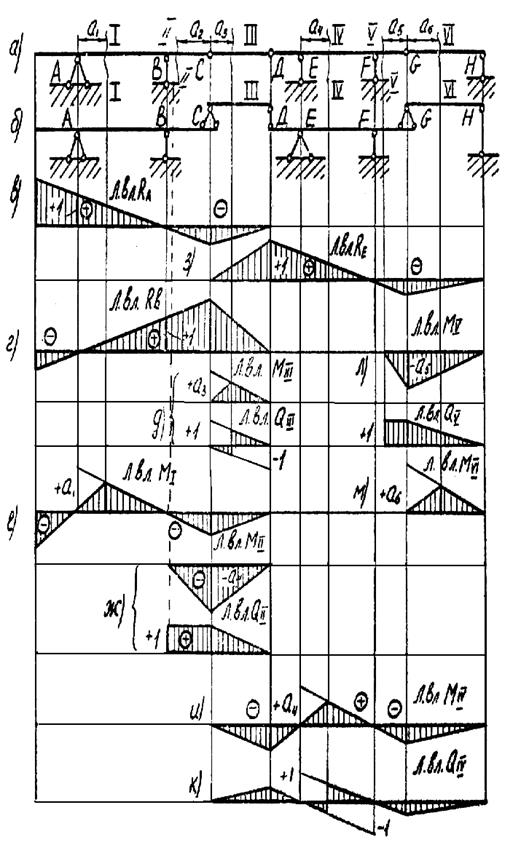
Рис. 3.20. Построение линий влияния опорных реакций, изгибающих моментов и поперечных сил для многопролетной балки в сечениях I, II, III, IV, V и VI