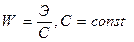СПОСОБЫ СКАЛЯРИЗАЦИИ ВЕКТОРНОГО КРИТЕРИЯ

Существуют два подхода к скаляризации векторного критерия - формализованная и неформализованная свертка.

В первом случае (формализованная свертка) для получения обобщенного показателя (обозначим его как U) используется некоторое формальное выражение, позволяющее по заданному значению вектора W_n={w₁,w₂...w_n}вычислить соответствующее ему значение обобщенного показателя

U=F (W_n)= F (w₁,w₂...w_n), где Fнекоторая заданная функция.

Во втором случае (неформализованная свертка) различным значениям вектора W_n={w₁,w₂...w_n}ставится в соответствиезначение обобщенного показателя без использования функциональных (формализованных) зависимостей. U=Y(W_n) = Y(w₁,w₂...w_n).

В дальнейшем, не снижая общности, будем обозначать сверткувекторного критерия в скаляр как U=U(W_n)=U(w₁,w₂...w_n).

На практике наиболее употребительны два метода свертки показателей: аддитивная и мультипликативная.

В аддитивной свертке обобщенный показатель эффективности представляется в виде взвешенной суммы показателей.

В мультипликативной свертке обобщенный критерий представляю в форме некоторого произведения (отношения) показателей.

Рассмотрим эти способы свертки более подробно.

Критерий «взвешенной суммы»

B этом случае обобщенный показатель U представляется в виде суммы показателей с весовыми коэффициентами a_i, которые также называются коэффициентами важности. Они отражают ценность i-ого показателя (его важность для обобщенного показателя) по сравнению с остальными.

Наиболее употребителен следующий вид свертки:

_n

U =å a_i u_i

ⁱ⁼¹

Здесь u_i -нормированное значение показателя w_i, равное его отношению к размеру области возможных значений. Чем ближе значение u_i к 1, тем выше качество, достигнутое по этому показателю. Нормировка вводится потому, что все слагаемые суммы должны иметь одинаковую размерность, иначе их нельзя было бы складывать. В рассмотренном случае в качестве скаляризованного критерия используется среднее взвешенное значение показателей.

Для весовых коэффициентов так же вводится условие нормировки в виде: åa_i=1. Значения весовых коэффициентов a_i назначаются экспертами или ЛПР, либо непосредственно, либо с помощью специальных процедур, которые позволяют учесть противоречия между весами различных показателей.

Процедура непосредственного назначения экспертами или ЛПР хороша тем, что она прозрачна и наилучшим образом отражает систему ценностей лица ее осуществляющего. Однако она возможна только, если размерность векторного критерия невелика. В противном случае она может оказаться трудно выполнимой.

В качестве специальной процедуры назначения весовых коэффициентов часто используют так называемой “метод парных сравнений” (МПС).

В основу МПС положена квадратная матрица, строки и столбцы которой отвечают упорядоченным последовательностям показателей w_i. Элементы матрицы а_ij показывают - на сколько (для аддитивный свертки) или во сколько раз (для мультипликативной свертки) i-й показатель важнее j – го и назначаются экспертами или ЛПР для каждой пары показателей. При аддитивной свертке сумма весовых коэффициентов в каждой паре должна быть равна 1: (a_ij + a_ji = 1). При мультипликативной свертке произведение весовых коэффициентов в парах равно 1: (a_ij * a_ji = 1).

Обработка заполненной матрицы позволяет получить искомые нормированные коэффициенты важности a_i.

При непосредственном назначении всех элементов матрицы парных сравнений эксперты или ЛПР могут проявить непоследовательность суждений при сопоставлении отдельных пар, что приведет к несогласованности элементов матрицы и нарушению транзитивности соответствующих коэффициентов. В этом случае необходима коррекция сделанных назначений.

Однако, матрицу можно задать лишь первой строкой, и из условий симметрии и нормировки формально определить ее целиком.. Тогда она будет внутренне согласованной, но зато будет хуже отображать точку зрения ЛПР или эксперта.

Критерий «эффективность - стоимость»

Формально этот критерий есть мультипликативная свертка двумерного вектора, и его можно было бы рассматривать в рамках сверток такого типа. Однако, его популярность настолько велика, что он заслуживает отдельного рассмотрения. Его широкое хождение, в первую очередь объясняется тем, что он очень прост и прозрачен. В самом деле, отношение эффективности принимаемого решения к затратам на его реализацию показывает, с одной стороны, насколько оправданы производимые вложения и, с другой стороны, во что может обойтись неоправданная экономия средств. Однако, заложенная в нем идеология не столь проста, как кажется на первый взгляд. Дело в том, что зависимость критерия от эффективности линейная, а от стоимости гиперболическая. В силу этого он отдает явное предпочтение дешевым решениям (проектам), а в дорогих относится к затратам весьма «снисходительно». Это хорошо иллюстрируют кривые на рис.1.

Рис.1.

При обращении к критерию «эффективность-стоимость» ЛПР должен внимательно относится к тому, насколько критерий отвечает пользовательскому пониманию задачи, и корректировать его особенности путем ограничений типа: «стоимость не выше, чем…», «эффективность не ниже, чем…».