Регрессионный анализ. 1 страница
При регрессионном анализе ставится задача отыскания функциональной зависимости математического ожидания отклика M(Y) от значений одного или нескольких факторов: M(Y)=f(Xl)или M(Y)=f(Xl,X2)и т.д.
Для чего это нужно? По крайней мере, для решения двух задач:
- прогнозирования значения функции отклика при некотором наборе значений факторов;
- для решения различных оптимизационных задач, связанных с данным процессом. Как известно, экстремум функции легко найти, если функция задана аналитически.
Искомая функция называется регрессионной моделью Y на X, а ее параметры - коэффициентами регрессии.
Не существует стандартных, формализованных методов, позволяющих только на основании результатов эксперимента установить теоретическую регрессию - истинную функциональную зависимость, отражающую действительную связь между откликом и контролируемыми факторами, не искаженную влиянием погрешностей измерения и неконтролируемыми факторами. Эту зависимость обычно ищут лишь в некотором классе функций, например, полиномиальных:
Y = a0 + a1·x + a2·x2
или степенных:
Y = a0·x1a1· x2a2
Пример 3.
Проводится эксперимент по исследованию процессов горения частиц древесного топлива на установке механотрон. Ставится задача отыскания аналитической зависимости массы частицы топлива от времени пребывания ее в зоне высоких температур:
m = f(t).
Итак, цель эксперимента должна быть сформулирована в терминах одной из трех задач: проверка статистических гипотез, дисперсионный анализ, регрессионный анализ.
4.3 Параметр оптимизации (Отклик). Обобщенный параметр оптимизации.
Выбор параметров оптимизации (критериев оптимизации) является одним из главных этапов работы на стадии предварительного изучения объекта исследования, т.к. правильная постановка задачи зависит от правильности выбора параметра оптимизации, являющегося функцией цели.
Под параметром оптимизации понимают характеристику цели, заданную количественно. Параметр оптимизации является реакцией (откликом) на воздействие факторов, которые определяют поведение выбранной системы.
Реальные объекты или процессы, как правило, очень сложны. Они часто требуют одновременного учета нескольких, иногда очень многих, параметров. Каждый объект может характеризоваться всей совокупностью параметров, или любым подмножеством этой совокупности, или одним — единственным параметром оптимизации. В последнем случае прочие характеристики процесса уже не выступают в качестве параметра оптимизации, а служат ограничениями. Другой путь - построение обобщенного параметра оптимизации как некоторой функции от множества исходных.
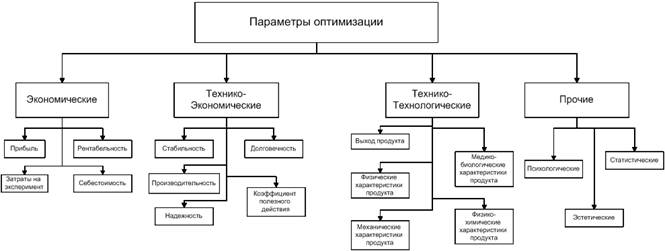
Рисунок 4.2 – Классификация параметров оптимизации
Требования к параметру оптимизации
- он должен быть количественным, задаваться числом;
- параметр оптимизации должен выражаться одним числом;
- однозначность в статистическом смысле;
- оценивал эффективность функционирования системы с точки зрения достижения цели;
- универсальность или полноты. Под универсальностью параметра оптимизации понимается его способность всесторонне характеризовать объект;
- имел физический смысл, был простым и легко вычисляемым.
Параметр оптимизации - это признак, по которому оптимизируется процесс. Он должен быть количественным, задаваться числом. Множество значений, которые может принимать параметр оптимизации, называется областью его определения. Области определения могут быть непрерывными и дискретными, ограниченными и неограниченными. Например, выход реакции — это параметр оптимизации с непрерывной ограниченной областью определения. Он может изменяться в интервале от 0 до 100%. Число бракованных изделий, число зерен на шлифе сплава, число кровяных телец в пробе крови - вот примеры параметров с дискретной областью определения, ограниченной снизу.
Количественная оценка параметра оптимизации на практике не всегда возможна. В таких случаях пользуются приемом, называемым ранжированием. При этом параметрам оптимизации присваиваются оценки - ранги по заранее выбранной шкале: двухбалльной, пятибалльной и т.д. Ранговый параметр имеет дискретную ограниченную область определения. В простейшем случае область содержит два значения (да, нет; хорошо, плохо). Это может соответствовать, например, годной продукции и браку.
Итак, первое требование: параметр оптимизации должен быть количественным.
Второе требование: параметр оптимизации должен выражаться одним числом.Иногда это получается естественно, как регистрация показания прибора. Например, скорость движения машины определяется числом на спидометре. Часто приходится проводить некоторые вычисления. Так бывает при расчете выхода реакции. В химии часто требуется получать продукт с заданным отношением компонентов, например, А:В=3:2. Один из возможных вариантов решения подобных задач состоит в том, чтобы выразить отношение одним числом (1,5) и в качестве параметра оптимизации пользоваться значением отклонений (или квадратов отклонений) от этого числа.
Третье требование,связанное с количественной природой параметра оптимизации - однозначностьв статистическом смысле. Заданному набору значений факторов должно соответствовать одно значение параметра оптимизации, при этом обратное неверно: одному и тому же значению параметра могут соответствовать разные наборы значений факторов.
Четвертым, наиболее важным требованием, требованием к параметрам оптимизации является его возможность действительно эффективной оценки функционирования системы. Представление об объекте не остается постоянным в ходе исследования. Оно меняется по мере накопления информации и в зависимости от достигнутых результатов. Это приводит к последовательному подходу при выборе параметра оптимизации. Так, например, на первых стадиях исследования технологических процессов в качестве параметра оптимизации часто используется выход продукта. Однако в дальнейшем, когда возможность повышения выхода исчерпан, начинают интересоваться такими параметрами, как себестоимость, чистота продукта и т.д.
Оценка эффективности функционирования системы может осуществляться как для всей системы в целом, так и оценкой эффективности ряда подсистем, составляющих данную систему. Но при этом необходимо учитывать возможность того, что оптимальность каждой из подсистем по своему параметру оптимизации «не исключает возможность гибели системы в целом». Это означает, что попытка добиться оптимума с учетом некоторого локального или промежуточного параметра оптимизации может оказаться неэффективной или даже привести к браку.
Пятое требованиек параметру оптимизации - требование универсальности или полноты.Под универсальностью параметра оптимизации понимают его способность всесторонне охарактеризовать объект. В частности, технологические параметры недостаточно универсальны: они не учитывают экономику. Универсальностью обладают, например, обобщенные параметры оптимизации, которые строятся как функции от нескольких частных параметров.
Шестое требование: желательно, чтобы параметр оптимизации имел физический смысл, был простым и легко вычисляем.
Требование физического смысла связано с последующей интерпретацией результатов эксперимента. Не представляет труда объяснить, что значит максимум извлечения, максимум содержания ценного компонента. Эти и подобные им технологические параметры оптимизации имеют ясный физический смысл, но иногда для них может не выполняться, например, требование статистической эффективности.
Второе требование, т.е. простота и легко вычисляемость, также весьма существенны. Для процессов разделения термодинамические параметры оптимизации более универсальны. Однако на практике ими пользуются мало: их расчет довольно труден.
Из приведенных двух требований первое является более существенным, потому что часто удается найти идеальную характеристику системы и сравнить ее с реальной характеристикой.
4.3.1 Задачи с несколькими выходными параметрами.
На практике чаще всего приходится учитывать несколько выходных параметров.
Поэтому из многих выходных параметров выбирается один в качестве параметра оптимизации, а остальные служат ограничениями. Всегда полезно исследовать возможность уменьшения числа выходных параметров. Для этого можно воспользоваться корреляционным анализом.
Если обозначить один параметр через y1 , а другой - через у2 , и число опытов, в которых они будут измеряться, - через N так, что u = l,2,...,N, где и — текущий номер опыта, то коэффициент парной корреляции r вычисляется по формуле (4.3) и (4.4).
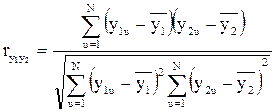 , (4.3)
, (4.3)
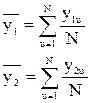 . (4.4)
. (4.4)
Значения коэффициента парной корреляции могут лежать в пределах от -1 до +1. Если с ростом значения одного параметра возрастает значение другого, у коэффициента будет знак плюс, а если уменьшается, то минус. Чем ближе найденное значение ry1y2к единице, тем сильнее значение одного параметра зависит от того, какое значение принимает другой, т.е. между такими параметрами существует линейная связь, и при изучении процесса можно рассматривать только один из них. Необходимо помнить, что коэффициент парной корреляции как мера тесноты связи имеет четкий математический смысл только при линейной зависимости между параметрами и в случае их нормального распределения.
Если экспериментально найденное значение r больше или равно критическому (приложение Б), то гипотеза о корреляционной линейной связи подтверждается, а если меньше, то нет оснований считать, что имеется тесная линейная связь между параметрами.
Каждый отклик имеет свой физический смысл и свою размерность. Чтобы объединить различные отклики, прежде всего приходится ввести для каждого из них некоторую безразмерную шкалу. Шкала должна быть однотипной для всех объединяемых откликов это делает их сравнимыми.
После построения для каждого отклика безразмерной шкалы, возникает следующая трудность - выбор правила комбинирования исходных частных откликов в обобщенный показатель. Единого правила не существует.
4.3.2 Простейшие способы построения обобщенного отклика.
Пусть исследуемый объект характеризуют n частных откликов yu (u = 1, 2 … n)и каждый из этих откликов измеряется в N опытах. Тогда yui - это значение u-го отклика в i-ом опыте (г = 1,2,..., N). Каждый из откликов уиимеет свой физический смысл и, чаще всего, разную размерность. Введем простейшее преобразование: набор данных для каждого yи поставим в соответствие с самым простым стандартным аналогом - шкалой, на которой имеется только два значения:
0 - брак, неудовлетворительное качество,
1 - годный продукт, удовлетворительное качество.
Стандартизовав таким образом шкалу частных откликов приступаем ко второму этапу - их обобщению.
В ситуации, когда каждый преобразованный частный отклик принимает только два значения 0 и 1, желательно чтобы и обобщенный отклик принимал одно из этих двух возможных значений, причем так, чтобы значение 1 имело место, если все частные отклики в этом опыте приняли значение 1. А если хотя бы один из откликов обратился в 0, то и обобщенный отклик будет нулем.
При таких рассуждениях для построения обобщенного отклика удобно воспользоваться формулой (4.5).
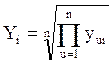 , (4.5)
, (4.5)
где Yi - обобщенный отклик в i-ом опыте;
 - произведение частных откликов y1i, y2i … yni,
- произведение частных откликов y1i, y2i … yni,
Недостаток этого подхода его грубость и жесткость.
4.3.3 Шкала желательности.
Одним из наиболее удобных способов построения обобщенного отклика является обобщенная функция желательности Харрингтона. В основе построения этой обобщенной функции лежит идея преобразования натуральных значений частных откликов в безразмерную шкалу желательности или предпочтительности. Шкала желательности относится к психофизическим шкалам. Ее назначение — установление соответствия между физическими и психологическими параметрами. Здесь под физическими параметрами понимаются всевозможные отклики, характеризующие функционирование исследуемого объекта. Среди них могут быть эстетические и даже статистические параметры, а под психологическими параметрами понимаются чисто субъективные оценки экспериментатора желательности того или иного значения отклика.
Чтобы получить шкалу желательности, удобно пользоваться готовыми таблицами соответствии между отношениями предпочтения в эмпирической и числовой системах (табл.4.1.).
Таблица 4.1 Стандартные отметки на шкале желательности
| Желательность | Отметки на шкале желательности |
| Очень хорошо | 1,00-0,80 |
| Хорошо | 0,80-0,63 |
| Удовлетворительно | 0,63-0,37 |
| Плохо | 0,37-0,20 |
| Очень плохо | 0,20-0,00 |
Выбор отметок 0,63 и 0,37 объясняется удобством вычислений:
0,63 ≈ 1 – (1/е), (4.6)
0,37 ≈ (1/е). (4.7)
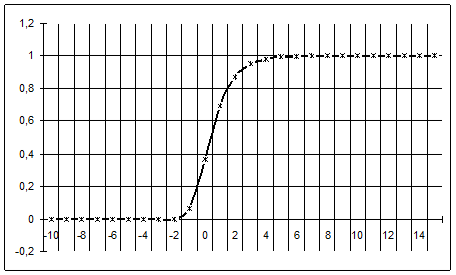
Рисунок 4.3 – График функции желательности
На оси ординат нанесены значения желательности d, изменяющиеся от 0 до 1, определяющиеся по формуле (4.8) . По оси абсцисс указаны значения отклика y, записанные в условном масштабе. За начало отсчета 0 по оси у выбрано значение, соответствующее желательности 0,37. Выбор именно этой точки связано с тем, что она является точкой перегиба кривой, что в свою очередь создает определенные удобства при вычислениях.
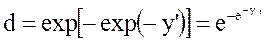 . (4.8)
. (4.8)
Значения на кодированной шкале принято выбирать от 3 до 6, причем выбор числа интервалов определяет крутизну кривой в средней зоне.
Такая кривая теоретически полностью выполняет функцию перевода откликов в безразмерный параметр, однако при практическом её использовании возникает ряд трудностей.
Во-первых, параллельно кодированной шкале y необходимо размещать именованные шкалы откликов Y1, Y2, …, которые следует калибровать в точках, указанных в таблице 4.1. и эта калибровка происходит достаточно произвольно. При этом почти всегда получается неравномерная школа.
4.3.4 Обобщенная функция желательности.
После выбора шкалы желательности и преобразования частных откликов в частные функции желательности приступают к построению обобщенной функции желательности. Обобщают по формуле (4.9).
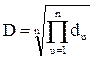 , (4.9)
, (4.9)
где D - обобщенная желательность;
du - частные желательности.
Способ задания обобщенной функции желательности таков, что если хотя бы одна желательность du= 0, то обобщенная функция будет равна нулю. С другой стороны D=l только тогда, когда du = 1. Обобщенная функция весьма чувствительна к малым значениям частных желательностей, определяющихся по формуле (4.8).
Обобщенная функция желательности является некоторым абстрактным построением, но она обладает такими важными свойствами, как адекватность, статистическая чувствительность, эффективность, причем эти свойства не ниже, чем таковые для любого технологического показателя, им соответствующего.
Обобщенная функция желательности является количественным, однозначным, единым и универсальным показателем качества исследуемого объекта и, обладая такими свойствами, как адекватность, эффективность, статистическая чувствительность, и поэтому может использоваться в качестве критерия оптимизации.
4.4 Факторы
После выбора объекта исследования и параметра оптимизации нужно рассмотреть все факторы, которые могут влиять на процесс. Если какой-либо существенный фактор окажется неучтенным и принимал произвольные значения, не контролируемые экспериментатором, то это значительно увеличит ошибку опыта. При поддержании этого фактора на определенном уровне может быть получено ложное представление об оптимуме, т.к. нет гарантии, что полученный уровень является оптимальным.
С другой стороны большое число факторов увеличивает число опытов и размерность факторного пространства (см. формулу 4.2).
Итак, выбор факторов является весьма существенным, т.к. от этого зависит успех оптимизации.
4.4.1 Характеристика факторов.
Фактором называется измеряемая переменная величина, принимающая в некоторый момент времени определенное значение и влияющая на объект исследования.
Факторы должны иметь область определения, внутри которой задаются его конкретные значения. Фактор считается заданным если вместе с его названием указана область его определения.
Область определения – совокупность всех значений, которые может принимать фактор.
Область определения может быть:
- непрерывной;
- дискретной.
При планировании эксперимента значения факторов принимаются дискретными, что связано с уровнями факторов. В практических задачах области определения факторов имеют ограничения, которые носят либо принципиальный, либо технический характер.
Факторы разделяются на:
- количественные;
- качественные.
К количественным относятся те факторы, которые можно измерять, взвешивать и т.д. Время реакции, температура, концентрация веществ, скорость подачи и т.д.
Качественные факторы - это различные вещества, технологические способы, приборы, исполнители и т.п. Реагенты, кислоты, металлы и т.п.
4.4.2 Требования предъявляемые к факторам.
1. Управляемость - факторы должны быть управляемыми, это значит, что выбранное нужное значение фактора можно поддерживать постоянным в течение всего опыта.
2. Операциональность - чтобы точно определить фактор, нужно указать последовательность действий (операций), с помощью которых устанавливаются его конкретные значения.
3. Точность замеров факторов должна быть возможно более высокой. Степень точности определяется диапазоном изменения факторов. В длительных процессах, измеряемых многими часами, минуты можно не учитывать, а в быстрых процессах приходится учитывать доли секунды.
4. Однозначность - факторы должны быть однозначны. Трудно управлять фактором, который является функцией других факторов. Но в планировании могут участвовать другие факторы, такие, как соотношения между компонентами, их логарифмы и т.п.
5. Совместимость - при планировании эксперимента одновременно изменяют несколько факторов, поэтому необходимо знать требования к совокупности факторов. Прежде всего выдвигается требование совместимости. Совместимость факторов означает, что все их комбинации осуществимы и безопасны.
6. Независимость - при планировании эксперимента важна независимость факторов, т.е. возможность установления фактора на любом уровне вне зависимости от уровней других факторов. Если это условие невыполнимо, то невозможно планировать эксперимент.
4.5 Выбор модели
При планировании эксперимента используются математические модели исследования. Под математической моделью мы понимаем уравнение, связывающее параметр оптимизации с факторами. Это уравнение в общем виде можно записать так:
y = f(x1, х2 … хn, w) + ε
Выбрать модель - значит выбрать вид этой функции, записать ее уравнение. Тогда останется спланировать и провести эксперимент для оценки численных значений констант (коэффициентов) этого уравнения.
Наглядное, удобное воспринимаемое представление о функции отклика дает ее геометрический аналог - поверхность отклика. В случае многих факторов геометрическая наглядность теряется, т.к. переходит в абстрактное многомерное пространство, где у большинства исследователей нет навыка ориентирования. Приходится переходить на язык алгебры. Потому рассмотрим простые примеры — случаи с двумя факторами.
Пространство, в котором строится поверхность отклика, называется факторным пространством. Оно задается координатными осями, по которым откладываются значения факторов и отклика (параметра оптимизации).
Для этого достаточно располагать плоскость с декартовой системой координат. По одной оси будем откладывать значения одного фактора Х1, по другой оси значения другого фактора Х2.
Для факторов существуют области определения, т.е. у каждого фактора есть минимальное и максимальное возможные значения, между которыми он может изменяться либо непрерывно, либо дискретно. Если факторы совместимы, то границы образуют на плоскости прямоугольник, внутри которого лежат точки соответствующие состояниям «черного ящика» (рисунок 4.4). Пунктирными линиями обозначены границы областей определения каждого фактора, сплошными линиями – границы их совместной области определения.
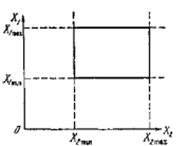
Рисунок 4.4 - Область определения факторов
Если требуется указать значения параметра оптимизации, требуется еще одна ось координат. Если ее построить, то поверхность отклика будет выглядеть так рисунок 4.5.
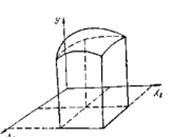
Рисунок 4.5 – Поверхность отклика трехмерном пространстве
Для двух факторов можно не переходить к трехмерному пространству, а ограничиться плоскостью. Для этого достаточно произвести сечения поверхности плоскостями, параллельными плоскости Х10Х2 и полученные в сечениях линии спроектировать на эту плоскость. Здесь каждая линия соответствует постоянному значению параметра оптимизации. Такая линия называется линией равного отклика.
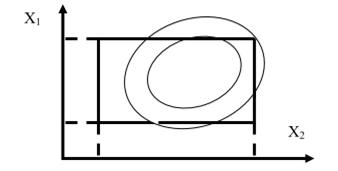
Рисунок 4.6 - Поверхность отклика на плоскости
Получив некоторое представление о модели, рассмотрим требования к ним:
- способность предсказывать направление дальнейших опытов;
- простота модели.
Главное требование к модели - это способность предсказывать направление дальнейших опытов, причем предсказывать с требуемой точностью. Это значит, что предсказанное с помощью модели значение отклика не отличается от фактического больше, чем на некоторую заранее заданную величину. Модель, отвечающая этому требованию, называется адекватной. Проверка выполнимости этого требования называется проверкой адекватности моделии она выполняется при помощи специальных статистических методов, которые будут рассмотрены позже.
Следующим требованием является простота модели. Но простота - вещь относительная, ее сначала надо сформулировать. При планировании эксперимента принимается, что простыми являются алгебраические полиномы (4.10) и (4.11). Наиболее часто применяются приведенные ниже полиномы.
Полином первой степени
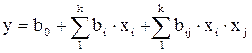 , (4.10)
, (4.10)
полином второй степени
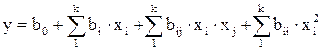 , (4.11)
, (4.11)
где у – значение критерия;
bi – линейные коэффициенты;
bij – коэффициенты двойного взаимодействия;
xi – кодированные значения факторов.
Эксперименты при планировании эксперимента нужны для определения численных значений коэффициентов. Чем больше коэффициентов, тем больше нужно опытов. А мы стремимся сократить их число. Следовательно, нужно найти такой полином, который содержит как можно меньше коэффициентов, но удовлетворяет требованиям, предъявляемым к модели.
Полиномы первой степени имеют наименьшее число коэффициентов, кроме этого они позволяют предсказывать направление наискорейшего улучшения параметра оптимизации. Но полиномы первой степени не эффективны в области близкой к оптимуму. Поэтому при планировании эксперимента на первой стадии исследовании используют полиномы первой степени, и когда они станут неэффективными, переходят к полиномам более высоких степеней.
4.5.1 Шаговый принцип.
За отказ от полного перебора состояний надо чем-то платить. Цена – это предположения, которые мы должны сделать относительно свойств неизвестной нам модели до начала эксперимента.
Главное предположение – это непрерывность поверхности, ее гладкость и наличие единственного оптимума (быть может, и на границе области определения факторов).
Эти постулаты позволяют представить изучаемую функцию в виде степенного ряда в окрестности любой возможной точки факторного пространства (такие функции в математике называются аналитическими). Кроме того, если мы придумаем какой-то способ постепенного приближения к оптимальной точке, нужно, чтобы результат не зависел от исходной точки.
Так как мы заранее считаем, что предпосылки выполняются, то надо максимально использовать возможности, которые при этом открываются.
Если, например, мы будем знать значения параметра оптимизации в нескольких соседних точках факторного пространства, мы сможем (в силу гладкости и непрерывности функции отклика) представить себе результаты, которые можно ожидать в других соседних точках. Следовательно, можно найти такие точки, для которых ожидается наибольшее увеличение (или уменьшение, если мы ищем минимум) параметра оптимизации. Тогда ясно, что следующий эксперимент надо переносить именно в эти точки. Надо продвигаться в этом направлении, пренебрегая остальными. Сделав новый эксперимент, снова можно оценить направление, в котором следует двигаться. В силу единственности оптимума мы, таким образом, рано или поздно непременно его достигнем. Это и есть шаговый принцип.
Сделаем некоторые пояснения. Мы выбираем в факторном пространстве какую-то точку и рассматриваем множество точек в ее окрестности, т. е. выбираем в области определения факторов малую подобласть. Здесь мы хотим провести эксперимент, на основании которого должна быть построена первая модель. Эту модель мы намерены использовать для предсказания результатов опытов в тех точках, которые не входили в эксперимент. Если эти точки лежат внутри нашей подобласти, то такое предсказание называется интерполяцией, а если вне – экстраполяцией. Чем дальше от области эксперимента лежит точка, для которой мы хотим предсказать результат, теме меньшей уверенностью это можно делать. Поэтому мы вынуждены экстраполировать недалеко и использовать результаты экстраполяции для выбора условий проведения следующего эксперимента. Дальше цикл повторяется.
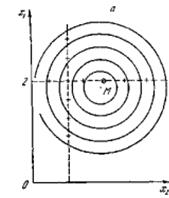
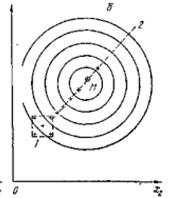
а – метод покоординатной оптимизации; б - пошаговый метод
Рисунок 4.7 - Два способа поиска оптимума
На рисунке 4.7 изображены два варианта поиска оптимума для одной и той же поверхности
- метод Гаусса-Зейделя (покоординатной оптимизации);
- пошаговый метод.
Метод Гаусса-Зейделя заключается в том, что сначала последовательно изменяют значения одного фактора, находится и фиксируется значение этого фактора и в этих условиях изменяется значение другого фактора.
Пошаговый метод заключается в том, что сначала изучается локальная область 1, затем определяется наиболее интересное направление и в этом направлении ставятся следующие опыты.
Попутно полученную модель можно использовать для проверки различных гипотез о механизме изучаемого явления или о его отдельных сторонах. Например, если вы предполагаете, что увеличение значения некоторого фактора должно приводить к увеличению значения параметра оптимизации, то с помощью модели можно узнать, так ли это. Такая проверка называется интерпретацией мидели.
Симплексный метод планирования
Метод симплексного планирования позволяет без предварительного изучения влияния факторов найти область оптимума. В этом методе не требуется вычисление градиента функции отклика. Для этого используется специальный план эксперимента в виде симплекса.
Дата добавления: 2017-12-05; просмотров: 3424;
