Вариация количественного признака
Средняя величина не дает исчерпывающей характеристики изучаемой совокупности. Возникает необходимость изучения характера рассеивания признака, т.е. его вариации.
Термин «вариация» происходит от латинского и обозначает – изменения, колеблемость.
Вариация – это различие в значениях какого-либо признака у разных единиц совокупности в один и тот же период или момент времени. Например, работники одного предприятия различаются по доходам, росту, весу, хобби и т.д.
Величины признаков варьируют под действием различных причин и условий, которые в статистике называются факторами. Среди них есть существенные факторы, определяющие величину вариантов данного признака у всех единиц совокупности, и несущественные, которые на одни единицы совокупности могут оказывать влияние, на другие нет. Например, вариация оценок студентов на экзамене в вузе вызывается, в частности, различными способностями студентов; временем, затраченным ими на самостоятельную работу; посещаемостью занятий и т.д. Но на оценку могут влиять и какие-либо случайные причины, например, временное недомогание.
Вариация, порождаемая существенными факторами, называется систематической, а вариация, обусловленная случайными факторами, - случайной.
Вариация зависимого признака, образовавшаяся под действием всех без исключения влияющих на него факторов, называется общей вариацией.
Для оценки вариации признака используют специальные показатели, которые делятся на две группы: абсолютные и относительные.
К абсолютным показателям вариации относятся:
1. Размах вариации рассчитывается как разность между максимальной и минимальной величиной признака:
R = xmax – xmin.
2. Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных отклонений признака от его среднего уровня.
| простое | взвешенное |
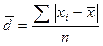
| 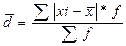
|
2. Дисперсия – это средний квадрат отклонений вариантов от их средней величины.
| простая | взвешенная |
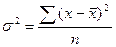
| 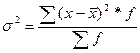
|
Формулу простой дисперсии можно преобразовать следующим образом:
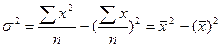 .
.
Такой метод вычисления дисперсии называется методом моментов.
4. Среднее квадратическое отклонение равно корню квадратическому из дисперсии: 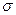 =
= 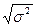 и показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения.
и показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения.
| простое | взвешенное |
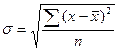
| 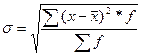
|
При сравнении вариации различных признаков в одной и той же совокупности или при сравнении вариации одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации или рассеивания:
1. Коэффициент осцилляции – определяется как отношение размаха вариации к средней величине признака и характеризует относительную рассеянность или колеблемость крайних значений признака вокруг средней. Он показывает, на сколько процентов отклоняется среднее от крайних значений вариации. Если 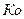 >100, то
>100, то 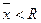 (крайних значений признака) и наоборот.
(крайних значений признака) и наоборот.
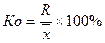 .
.
2. Относительное отклонение – определяется путем деления среднего линейного отклонения на среднюю величину:
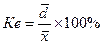
3. Коэффициент вариации используется также для характеристики однородности совокупности. Совокупность считается однородной, если ее коэффициент вариации не превышает 33%.
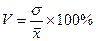 .
.
Дата добавления: 2017-11-04; просмотров: 671;
