Теореми Бернуллі та Пуассона

У найбільш простій формі закон великих чисел сформулював і довів у кінці ХYII сторіччя Яків Бернуллі. Теорема Бернуллі є наслідком теореми Чебишева, котра формулює закон великих чисел у схемі Бернуллі.

Теорема Бернуллі. Частість події в 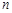незалежних випробуваннях, у кожному з яких вона може відбутися з ймовірністю 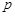, при необмеженому збільшенні числа 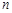збігається за ймовірністю до ймовірності 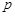цієї події в кожному випробуванні, тобто

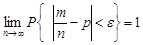. (25.2)

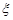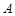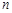Доведення. Нехай випадкова величина задає загальну кількість появ події в незалежних випробуваннях. Введемо випадкові величини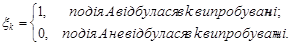

Тоді 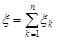, математичне сподівання 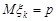, дисперсія 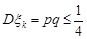, 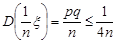. Із нерівності Чебишева маємо

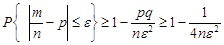. (25.3)

Переходячи до границі при 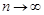, маємо формулу (25.2).

Узагальненням теореми Бернуллі є теорема Пуассона.

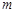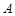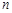Теорема Пуассона. Якщо – кількість появ події в незалежних випробуваннях і – імовірність появи цієї події в 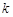-му випробуванні, то яким би не було число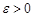

.

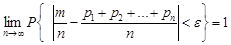Очевидно, що при 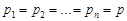маємо теорему Бернуллі. Доведення теореми Пуассона проведіть самостійно.

Приклад 25.3. Імовірність виготовлення нестандартної радіолампи дорівнює 0,04. Яке найменше число радіоламп треба відібрати, щоб з імовірністю 0,88 можна було б стверджувати, що доля нестандартних радіоламп серед них буде відрізнятися від імовірності виготовлення нестандартної радіолампи за абсолютним значенням не більше ніж на 0,02?

Розв’язання. З оцінки (25.3) дістанемо:

.

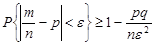За умовою задачі ймовірність p = 0,04, величина 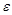= 0,02, звідки 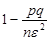= 0,88.

Отже, .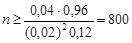

Теорема Маркова

П.Л.Чебишев знайшов умови, при яких спостерігається стійкість середнього арифметичного незалежних у сукупності випадкових величин. Пізніше багато робіт було присвячено з’ясуванню умов, які треба накласти на залежні випадкові події, щоб для них також виконувався закон великих чисел. Наведемо одне з таких узагальнень.

Теорема Маркова. Нехай задана послідовність 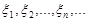випадкових величин, для яких М 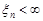та

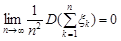. (25.4)

Тоді для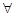

.

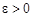
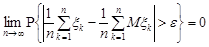Очевидно, теорема Чебишева є окремим випадком теореми Маркова. Дійсно, якщо випадкові величини 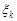– незалежні, крім того, 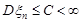, n = 1, 2,... , тоді

.

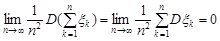Доведення теореми Маркова базується також на нерівності Чебишева. Згідно цієї нерівності

.

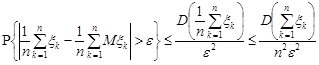Із умови (25.4) маємо висновок теореми Маркова.

Наприклад, температура повітря в деякій місцевості 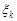( 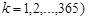кожний день року є випадковими величинами, причому залежними, оскільки, на погоду кожного дня впливає, очевидно, погода попередніх днів. Але середньорічна погода 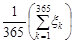для даної місцевості майже не міняється протягом багатьох років, отже, є практично невипадковою величиною.

Крім різних форм закону великих чисел має місце так званий “посилений закон великих чисел”, в якому встановлюється не “збіжність за ймовірністю”, а “збіжність із ймовірністю 1” різних середніх випадкових величин до невипадкових середніх.

Закон великих чисел і наслідки з нього лежать в основі чисельного метода, який називається “метод статистичних випробувань (метод Монте-Карло)”. Цей метод часто використовують для наближеного обчислення визначених інтегралів, для розв’язку систем лінійних алгебраїчних рівнянь високого порядку, при розв’язанні крайових задач для рівнянь в частинних похідних і багатьох інших задач чисельного аналізу.

Ідею методу статистичних випробувань покажемо на прикладі наближеного обчислення визначеного інтегралу від деякої функції .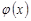

Нехай .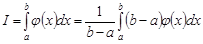

Значення цього інтегралу можна розглядати як математичне сподівання випадкової величини 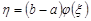, де випадкова величина 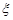розподілена рівномірно на проміжку 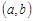. Нехай послідовність 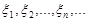незалежних випадкових величин має рівномірний розподіл на проміжку 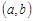. Існують стандартні програми, які модулюють послідовність випадкових величин, розподілених рівномірно на .

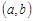Випадкову величину

,

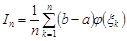згідно закону великих чисел, можна вважати наближеним значенням інтегралу.