Распределение Пуассона.
Если известны значения дискретной случайной величины, тогда закон распределения может быть законом Пуассона. Распределение Пуассона обычно использует в случае «редких событий», (например, определение родившихся двойняшек в городе за определенный период).
Пусть случайная величина Х, принимающая только целые положительные значения, распределена по закону распределения Пуассона с параметром λ, если:
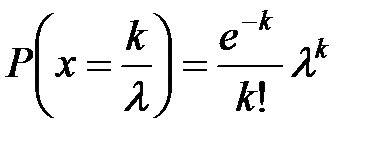 , (3.2)
, (3.2)
где 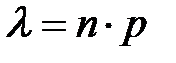 - интенсивность, n – количество испытаний (наблюдений); а p – вероятность появления события в каждом из них.
- интенсивность, n – количество испытаний (наблюдений); а p – вероятность появления события в каждом из них.
Нормальный закон распределения (НЗР)
НЗР вероятности случайной величины Х имеет место только для непрерывной случайной величины и задается плотностью вероятности
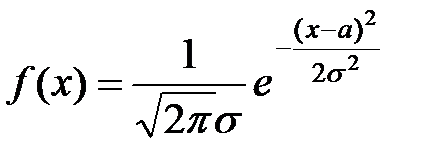 (3.3)
(3.3)
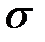 - среднее квадратное отклонение, а – математическое ожидание.
- среднее квадратное отклонение, а – математическое ожидание.
Обозначение нормальной случайной величины: 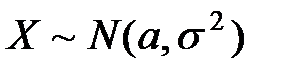 . Если
. Если 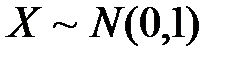 , нормальная случайная величина называется стандартной нормальной величиной. Плотность нормализированного распределения имеет вид
, нормальная случайная величина называется стандартной нормальной величиной. Плотность нормализированного распределения имеет вид 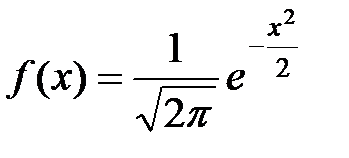 . Параметр а определяет положение центра нормальной плотности,
. Параметр а определяет положение центра нормальной плотности,  - разброс относительно центра.
- разброс относительно центра.
Свойства нормального распределения:
1. Для нормального распределения совпадают величины математического ожидания, моды и медианы.
2. Кривая плотности нормального распределения симметрична относительно средней а.
3. Если постоянно 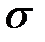 , а меняется а, то форма кривой остается неизменной, а ее график смещается вдоль оси абсцисс.
, а меняется а, то форма кривой остается неизменной, а ее график смещается вдоль оси абсцисс.
4. При постоянстве а изменение 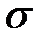 влечет изменение ширины и высоты кривой.
влечет изменение ширины и высоты кривой.
5. Площадь под нормальной кривой не зависит от а и 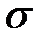 и всегда равна единице.
и всегда равна единице.
6. Вероятность попадания нормально распределенной величины в интервалы 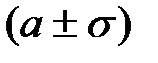 ,
, 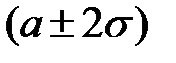 ,
, 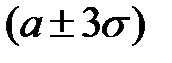 составляет 68.3%, 95.4% и 99.7% соответственно.
составляет 68.3%, 95.4% и 99.7% соответственно.
Нормальная кривая – это график плотности нормального распределения.
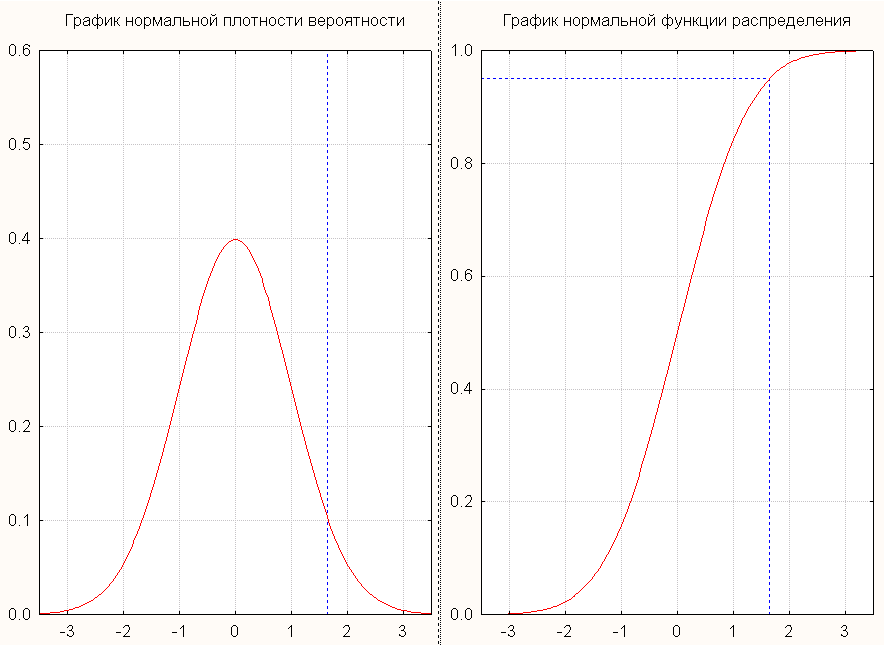
| 95.4% |
| 99.7% |
Дата добавления: 2017-02-20; просмотров: 362;
