Постановка основных краевых задач для уравнений Лапласа и Пуассона

Для решения уравнения Лапласа или Пуассона, как и вообще для решений стационарных задач, естественно, не задается начальный режим. Задаются лишь условия на границе области.

Математически задача для уравнений Лапласа (Пуассона) ставится так: найти функцию 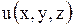, удовлетворяющую внутри области 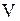, ограниченной замкнутой поверхностью 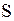, уравнению

( )

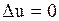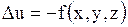и граничному условию, которое может быть взято в одном из следующих видов:

I. 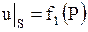(граничное условие 1-го рода);

II. 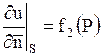(граничное условие 2-го рода);

III. 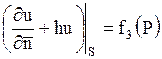(граничное условие 3-го рода),

где 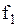, , 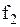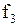- заданные непрерывные функции; 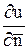- производная по внешней нормали 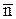к поверхности 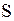; 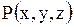- текущая точка поверхности.

Как отмечалось в п. 1.32, задача интегрирования уравнения Лапласа с граничным условием первого рода называется первой граничной задачей или задачей Дирихле, а с условием второго рода – второй граничной задачей или задачей Неймана. Если задана линейная комбинация неизвестной функции и ее нормальной производной, то задачу интегрирования называют третьей граничной задачей. В некоторых задачах на разных участках границы задаются условия разных типов, тогда говорят о смешанной граничной задаче.

В частности, если уравнение Лапласа описывает установившийся режим фильтрации, а функция 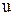определяет давление в каждой точке пласта, то граничное условие первого рода означает, что в точках поверхности 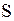задается давление (например, давление на забое скважины или на контуре питания при плоско-параллельном течении); задание граничного условия второго рода равносильно заданию потока фильтрующейся жидкости, т.е. дебита в каждой точке границы 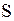. Граничное условие третьего рода задается, когда имеет место переток жидкости в выше – или нижележащие пласты.

Если решение ищется в области 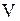, внутренней (или внешней) по отношению к поверхности 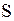, то соответствующую задачу называют внутренней (или внешней) граничной задачей.