областей методом разделения переменных

Для областей произвольной формы метод Фурье для решения уравнения Лапласа (или Пуассона) неприменим. Этот метод для уравнения Лапласа проходит лишь в случае некоторых простейших областей, где возможно разделение переменных в граничных условиях (прямоугольник, круг, кольцо, сектор, шар, цилиндр и др.) Получающиеся при этом задачи на собственные значения (задачи Штурма-Лиувилля) приводят к различным специальным функциям. Мы рассмотрим задачи Дирихле в плоской области, при решении которых используются только тригонометрические функции (круговые и гиперболические).

1.38.1. Решение задачи Дирихле (внутренней и внешней) для круга. Интеграл Пуассона

Прежде напомним определение: функция 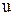называется гармоническойв некоторой области 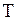, если она непрерывна в этой области вместе со своими частными производными до второго порядка включительно и удовлетворяет уравнению Лапласа в этой области. Решим первую граничную задачу (внутреннюю и внешнюю) для круга. Имея в виду, что различные физические процессы с математической точки зрения могут быть совершенно подобными, мы не будем интерпретировать рассматриваемую задачу в терминах того или иного физического явления, а ограничимся математической постановкой и разберем метод решения, единый для аналогичных проблем.

Внутренняя задача Дирихле: найти функцию 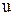, удовлетворяющую уравнению

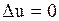
(1.260)

внутри круга 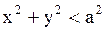, непрерывную в замкнутой области 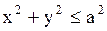и принимающую заданные значения на границе круга:

.

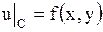(1.261)

Внешняя задача Дирихле: найти функцию, гармоническую в области 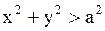(внешность круга), ограниченную в области 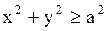и удовлетворяющую граничному условию (1.261).

Обе задачи будем решать одновременно. Задачу проще решать в полярной системе координат 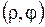, где

, .

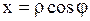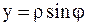(1.262)

После замены переменных (1.262) уравнение Лапласа

в полярных координатах принимает вид

.

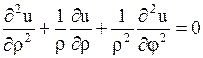(1.263)

(Читателю предоставляется выполнить это самостоятельно). Соответственно граничное условие (1.262) запишется так:

, .

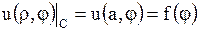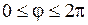(1.264)

Причем 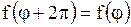, т.к. увеличение 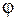на 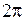возвращает точку 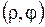в исходное положение.

Согласно методу Фурье ищем решение уравнения (1.263) при условии (1.264) в виде

.

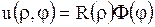(1.265)

Подставляя (1.265) в (1.263), получим

.

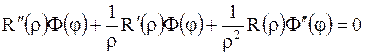Разделяем переменные

.

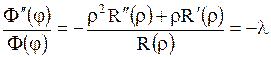Поскольку по обе стороны знака равенства стоят функции от различных независимых переменных, то такое равенство возможно только тогда, когда обе части равны одной и той же постоянной, которую обозначим через 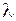. Тогда приходим к двум обыкновенным дифференциальным уравнениям:

,

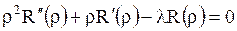(1.266)

.

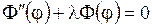(1.267)

Общее решение линейного уравнения (1.267) есть

.

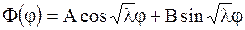(1.268)

При изменении угла 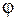на величину 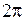однозначная функция 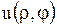, как и ограниченная функция 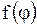, должна вернуться к исходному значению, т.е. должно быть выполнено условие периодичности:

.

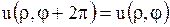Отсюда следует, что функция 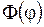является периодической с периодом :

.

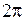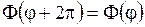(1.269)

Решение (1.268) будет удовлетворять условию периодичности лишь тогда, когда 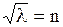, где 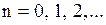Отрицательные 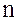можно отбросить, т.к. знак 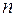влияет только на знак произвольной постоянной 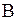. Значит, отрицательные 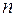не дают новых решений.

Таким образом, собственные числа и собственные функции задачи (1.268), (1.269) есть

, ,

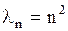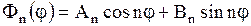(1.270)

Подставим теперь 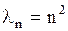в уравнение (1.266):

.

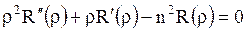(1.271)

В литературе уравнение (1.271) известно под названием уравнения Эйлера. Его решение ищут в виде

.

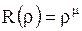(1.272)

Подставляя (1.272) в (1.271), найдем

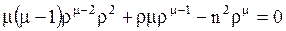
или, сокращая на ,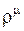

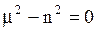, откуда .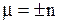

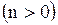Таким образом, для каждого значения 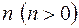имеется два линейно независимых решения 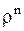и 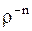, которые определяют свое общее решение 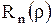уравнения (1.271):

,

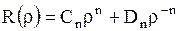(1.273)

где 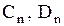- постоянные. Перемножая теперь 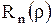и 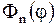, согласно (1.265), получим дискретную совокупность функций

.

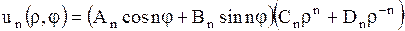(1.274)

Для внутренней задачи Дирихле надо положить 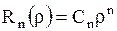, т.к. если 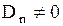, то функция (1.274) обращается в бесконечность при 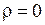и не является гармонической внутри круга 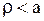. Для решения внешней задачи, наоборот, надо взять , иначе, положить 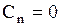, т.к. решение (1.274) должно быть ограниченным в области 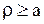. Тогда частными решениями уравнения (1.263) являются функции

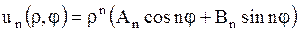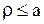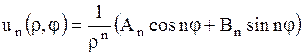для ,

для ,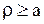

.

(Постоянные 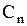и 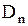включены в 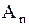и 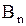). В силу линейности и однородности уравнения Лапласа суммы частных решений

, ,

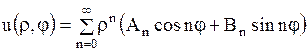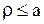(1.275)

,

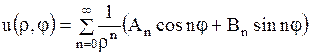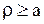
(1.276)

также будут решением уравнения Лапласа (при условии сходимости рядов).

Подберем произвольные постоянные 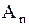и 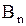так, чтобы удовлетворялось условие (1.264)

, .

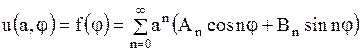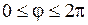(1.277)

Напишем ряд Фурье для периодической функции 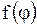на отрезке :

,

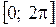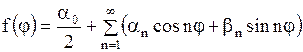(1.278)

где

,

,

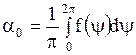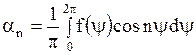(1.279)

.

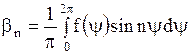Сопоставляя (1.277) и (1.278), заключаем, что для выполнения граничного условия (1.277) нужно положить 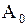, , 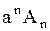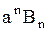равными коэффициентам Фурье:

, , .

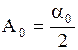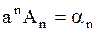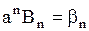Следовательно, для внутренней задачи

, , ,

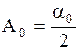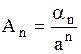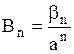для внешней задачи

, , .

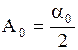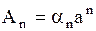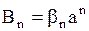Таким образом, решение внутренней задачи Дирихле для круга представим в виде ряда

,

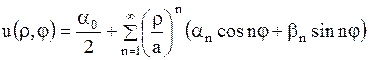(1.280)

а решение внешней задачи Дирихле в виде ряда

,

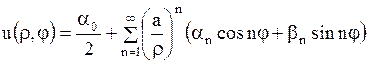(1.281)

где 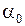, , 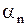определяются как коэффициенты ряда Фурье для функции 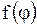по формулам (1.279).

Установлено, что так построенные функции (1.280) и (1.281) удовлетворяют всем условиям задачи.

Преобразуем формулы (1.280), (1.281) к более простому виду. Рассмотрим подробно внутреннюю задачу, а для внешней задачи получим результат по аналогии. Преобразуем ряд (1.280), подставив выражения для коэффициентов Фурье (1.279) и произведя затем перестановку порядка суммирования и интегрирования

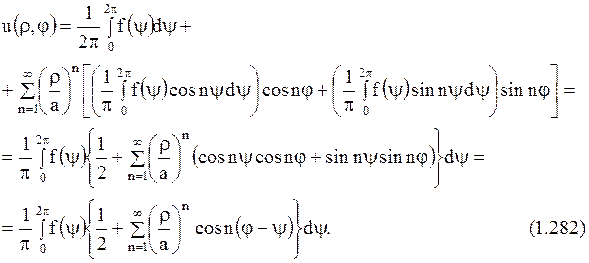
Произведем тождественные преобразования в фигурных скобках, обозначив для краткости 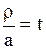, 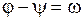; при этом воспользуемся формулой

,

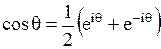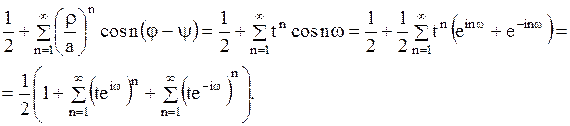
Ряд 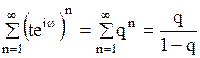является бесконечной геометрической прогрессией со знаменателем 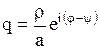, модуль которого 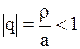. В силу этого имеем следующее представление:

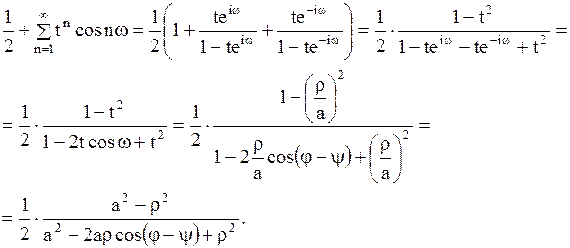
Подставляя полученный результат в (1.282), получаем

.

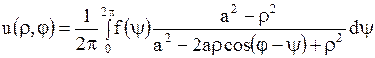(1.283)

Эта формула называется формулой Пуассона, а интеграл справа – интегралом Пуассона. Формула (1.283) позволяет записать искомое решение внутренней задачи Дирихле в форме интеграла, зависящего от параметров 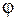и 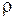. Он существует для всех значени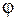й и 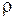, 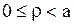и удовлетворяет уравнению (1.263), а также граничному условию (1.264). Заметим, однако, что интеграл (1.283) теряет смысл при 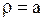. Когда говорят, что функция (1.283) удовлетворяет граничному условию, то под этим подразумевают, что 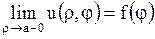. Поэтому решение внутренней задачи записывается так:

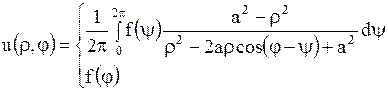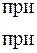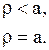
(1.284)

По аналогии решение внешней задачи имеет вид

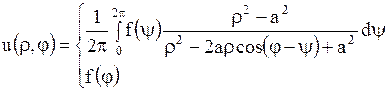
(1.285)

Замечание. Интеграл Пуассона дает решение плоской задачи Дирихле для круга. Но он может служить решением и пространственной задачи Дирихле в случае цилиндрической симметрии области, т.е. когда область есть бесконечный цилиндр, а искомая функция 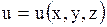, например, температура или электрический потенциал, не зависит от 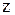. Тогда температура или потенциал в любом сечении, перпендикулярном к оси 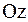, зависит только от 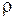и 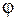. Следовательно, здесь имеет место плоская задача Дирихле.