Основное уравнение релятивистской динамики

В ньютоновой механике обычная трехмерная 3-сила определяется как скорость изменения во времени количества движения, переносимого на данное тело от окружающих тел и полей (равенство 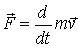Ньютона является одновременно и определением силы, и законом движения). Аналогично поступим и в релятивистской механике, не забывая в то же время, что делить (множить) следует только на инвариантные величины.

По определению 4-сила 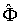- это скорость изменения 4-импульса, оцененная в течение собственного времени движущегося тела (точки; частицы), т.е. 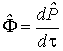. Подставляя значение 4-импульса, можно представить 4-силу в виде

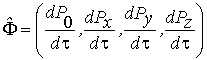
или

=

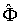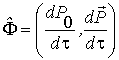
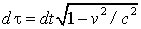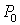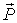Подставив значение и учтя явный вид компонент импульса и , получим величину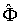

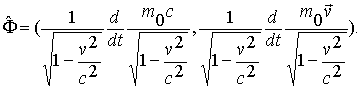
(1.17)

Так выглядит 4-сила в системе I (в которой время t, скорость 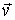). Ниже структура 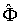будет представлена в более компактном виде.

Здесь возникает важный вопрос: если при скоростях значительно меньших скорости света, т.е. в ньютоновой механике, сила определяется по второму закону Ньютона равенством 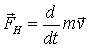(индекс "н" указывает на ньютонову механику), то как следует обобщить понятие 3-силы на любые скорости, вплоть до как угодно близких к скорости света?

Ответ на такие вопросы может давать только практика, эксперименты, опыт. Вся современная экспериментальная физика подтверждает, что под релятивистской 3-силой следует понимать величину, являющуюся производной от релятивистского 3 импульс

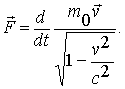
(1.18)

Это равенство обобщает ньютонову трактовку 3-силы. В то же время оно представляет основной закон движения частицы (материальной точки) в инерциальной системе отсчета при любых возможных скоростях меньших с.

Рассмотрим закон преобразования компонент 4-силы, представленных формулой (1.17). Учитывая (1.18), представим 4-силу в окончательном виде

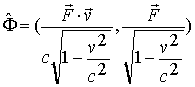
(1.19)

Как видим, в структуру 4-силы Минковского 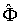входит релятивистская

трехмерная сила 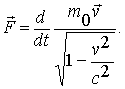и ее мощность .

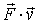Рассмотрим дальше преобразование компонент 4-силы при переходе от ИСО I к ИСО П, которая движется со скоростью v относительно системы I в направлении оси х. При этом в системе I предполагается известным мгновенное значение скорости точки 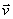(v_x,v_y,v_z) и сила 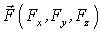. Преобразование 4-силы позволит определить также и величину трехмерной силы в системе II. Как уже указывалось, преобразование компонент 3-векторов определяется на основе сначала преобразования 4-векторов (при переходе 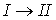). Итак, нужно подвергнуть компоненты 4-силы 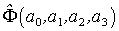, т.е.

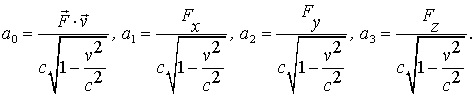
(1.20)

преобразованиям Лоренца.

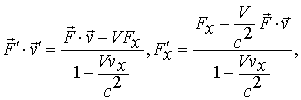
(1.20a)

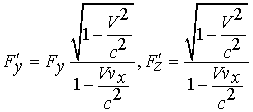
(1.20b)

Следовательно, при переходе от системы отсчет I к системе II проекции 3-силы 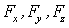изменяются; они остаются неизменными в нерелятивистском случае, когда 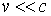. Первая из полученных формул определяет мощность силы в системе II, остальные три - проекции силы.

В ньютоновой механике работа силы равна приращению кинетической энергии: 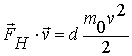. В СТО понятие силы обобщено, и работу релятивистской силы нужно заново вычислить. Найдем работу релятивистской силы 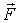на элементарном перемещении 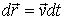частицы

.

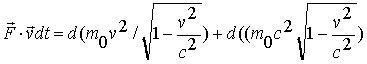Здесь использовано правило дифференцирования произведения функций; учтено что 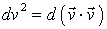и 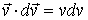. Объединяя оба слагаемые под одним дифференциалом, окончательно получаем

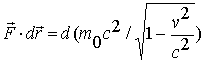
(1.21)

Найденное равенство показывает, что работа силы равна приращению величины 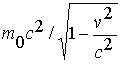. Поэтому последнюю следует истолковать как энергию движущегося тела (частицы):

(1.22)

Эта формула, установленная Эйнштейном в 1905 г., в начале прошлого столетия вызывала сомнение, а позже обеспечила полный триумф теории относительности. Формула (1.22) устанавливает связь между массой (покоя) и энергией тела при его скорости .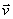

Из формулы Эйнштейна вытекает важное открытие 20 века: любое тело в состоянии покоя обладает колоссальной энергией, равной

.

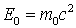(1.23)

Дадим определение: кинетической энергией тела называется разность

,

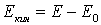откуда 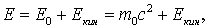или

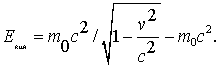
(1.24)

Формула (1.24) для энергии определяет сумму двух энергий: энергии покоя (она относится в внутренней энергии) 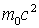и кинетической .

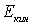Учитывая значения временной компоненты 4-импульса P₀ и полной энергии Е (формула, 4-импульс 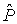можно представить в виде

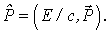
(1.25)

Как видим, в 4-импульсе объединились энергия Е и релятивистский 3-импульс 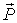, что означает глубокую внутреннюю связь между релятивистской энергией 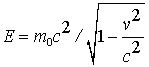и релятивистским импульсом 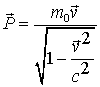. При переходе из одной инерциальной системы отсчета в другую значение каждой из четырех компонент 4-импульса 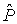определяется по формулам Лоренца через все четыре компоненты в исходной системе I. Например, значение энергии в системе II определяется не только через энергию в системе I, но и через все компоненты импульса .

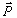Полезными являются также очевидные формулы для релятивистского импульса 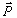и его модуля в виде:

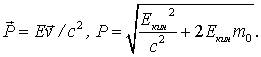
(1.26)

Определим величины, сохраняющиеся при переходе из одной системы отсчета в другую. Их обычно называются инвариантами. Как отмечалось, 4-импульсу 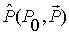соответствует инвариант

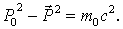
Подставляя значение 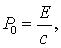получаем

(1.27)

Это соотношение между релятивистской энергией и релятивистским импульсом выполняется как для частицы" так и для тела, и даже для сложной системы, так как при его выводе нигде не использовалась неделимость объекта.

И общем случае в (1.27) под Е следует понимать полную энергию системы, а под 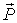- геометрическую сумму импульсов всех частей системы.

Равенство (1.27) можно рассматривать так же как определение инвариантной массы (массы покоя) любой физической системы

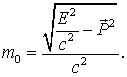
(1.28)

В частном случае системы отсчета, в которой импульс равен нулю ( 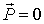), имеем

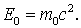
(1.29)

Следовательно, масса покоя тела определяет его энергию покоя (во всех ее видах). В релятивистской механике, в отличие от классической, энергия тела всегда положительна.

В другом частном случае, когда масса покоя равна нулю, 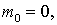соотношение (1.27) дает связь между релятивистским импульсом и энергией следующего вида

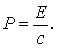
В частности, для фотона с нулевой массой покоя эта формула преобразуется к виду

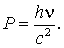
Вернемся к рассмотрению 4-импульса 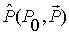. Он объединяет релятивистскую энергию 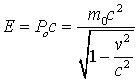с релятивистским импульсом 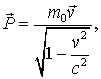а значит представляет собой некоторую новую (одну единую!) величину, которую можно определить термином энергия-импульс. 4-вектору энергия-импульс соответствует инвариант (1.27), играющий важную роль в атомной и ядерной физике

В случае изолированной физической системы эта величина сохраняется не только при переходе от системы отсчета I к системе II, но также сохраняется ее значение как до, так и после реакции, происходящей в физической системе.