Примеры решения задач по термодинамике.
Пример 1.1. Избыточное давление в паровом котле, измеренное пружинным манометром Ри = 2500 кПа. Барометрическое давление 765 мм.рт.ст. Определить абсолютное давление в котле.
Решение. Абсолютное давление в котле определяется по формуле 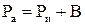 ;
;
1 мм.рт.ст. создает давление 133,32 Па, а 766 мм.рт.ст. соответствует давлению 101991,33 Па ≈102 кПа. Следовательно, абсолютное давление в котле:
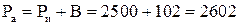 кПа = 2,6 МПа.
кПа = 2,6 МПа.
Пример 1.2. В резервуаре объемом 10 литров находится воздух при температуре 17 0С, и в избыточном давлении 0,1 ат. Сколько воздуха нужно откачать из резервуара, чтобы в нем создать вакуум 540 мм.рт.ст. Барометрическое давление 754 мм.рт.ст.
Решение. Масса удаленного воздуха находится как разность масс воздуха в баллоне до и после откачивания 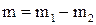
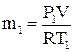 ;
; 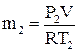 ,
,
Р1 и Р2 – абсолютное давление в резервуаре до и после удаления воздуха.
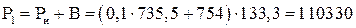 Па
Па
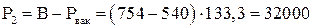 Па
Па
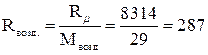 Дж/кг?К
Дж/кг?К
V = 0,01м3 ; Т1 = 17 + 273 = 290 К; Т2 = 27 + 273 = 300 К.
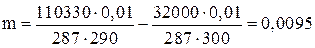 кг.
кг.
Пример 1.3. Объемные доли компонентов смеси идеальных газов: 20% СО2 , 20% N2 , 60% Н2. Давление смеси 2 МПа, температура 400 0С. Найти парциальные давления компонентов, их массовые доли, молярную массу и плотность смеси при нормальных условиях и условиях, указанных в задаче. Найти количество теплоты, которое необходимо отвести от 1 кг смеси, чтобы охладить ее до 0 0С при постоянном давлении.
Решение. Парциальное давление компонентов:
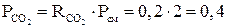 МПа = 400 кПа;
МПа = 400 кПа;
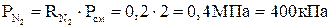 ;
;
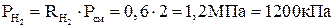 .
.
Молярная масса смеси:
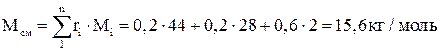 .
.
Массовые доли компонентов:
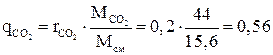 ,
,
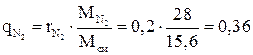 ,
,
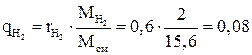 ,
,
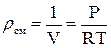 ,
,
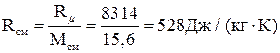 ,
,
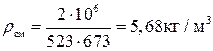 ,
,
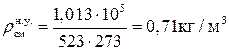 ,
,
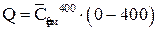 ,
,
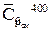 - средняя в интервале температур 0 – 400 0C массовая теплоемкость газовой смеси при постоянном давлении
- средняя в интервале температур 0 – 400 0C массовая теплоемкость газовой смеси при постоянном давлении
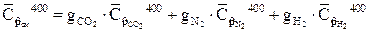
Средние массовые теплоемкости компонентов находим используя таблицу 2
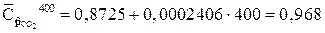 кДж/(кг?К)
кДж/(кг?К)
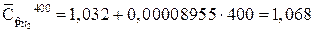 кДж/(кг?К)
кДж/(кг?К)
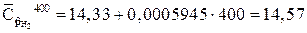 кДж/(кг?К)
кДж/(кг?К)
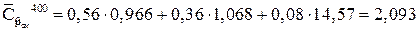 кДж/(кг?К)
кДж/(кг?К)
q = 2,093?(-400) = - 837 кДж/(кг?К)
Знак «-» показывает, что теплота отводится от газовой смеси.
Пример 1.4. В закрытом сосуде объемом 0,8 м3 находится двуокись углерода при
Р1 = 2,2 МПа и t1 = 20 0C. Газу сообщается 4600 кДж теплоты.
Определить температуру и давление двуокиси углерода в конце процесса.
Примечание. Теплоемкость считать не зависящей от температуры.
Решение: Количество теплоты, выраженное через теплоемкость и разность температур, равно:
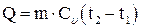 ,
,
отсюда
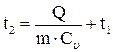 .
.
Масса газа
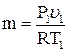 ,
,
где 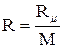 .
.
Массовую теплоемкость СО2 при постоянном объеме вычислим из мольной теплоемкости 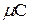 v (табл. ) для многоатомных газов
v (табл. ) для многоатомных газов
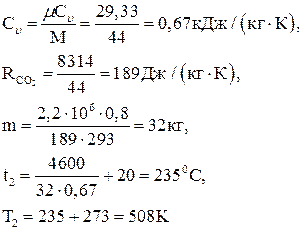
Давление в конечном состоянии
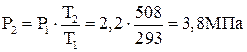 .
.
Пример 1.5. Кислород , имеющий массу 10 кг и температуру 27 0С при нагревании при постоянном давлении Р = 0,3 МПа увеличивает объем в 1,5 раза. Определить конечную температуру газа, работу и количество теплоты, изменение внутренней энергии и энтропии в этом процессе. Теплоемкость принять постоянной.
Решение:
Вычисляем конечную температуру:
T2 = T1(υ2 / υ1) = (27 + 273)1,5 = 450 0C
или
t2 = T2 - 273 = 177 0C
Находим работу расширения
L = m ? l = m ? R(T2 – T1) = 10 ? 8314 / 32(450 - 300) = 390 кДж.
Количество теплоты
Qp = m ? q = m ? Cp(t2 – t1) = m ? μCp / M(t2 – t1) = 10 ? (29,3 / 32)150 = 1373 кДж,
где мольная теплоемкость двухатомного газа μCp = 29,3 кДж/(моль? К).
Изменение внутренней энергии
ΔU = Qp – L = 1373 – 390 = 983 кДж.
Изменение энтропии
ΔS = m ?ΔS = m ? Cp ?ln(T2 / T1) = 10 ?(29,3 / 32)ln(450 / 300) = 31 кДж/К.
Пример 1.6. 25 кг воздуха при 27 0С изотермически сжимаются до тех пор, пока давление не становится равным 4,15 МПа. На сжатие затрачивается работа L = -8,0 МДж. Найти начальные давления и объем, конечный объем и теплоту, отведенную от воздуха.
Решение: Работа сжатия воздуха равна:
L = m ? RTln(P1 / P2)
отсюда:
lnP1 = lnP2 + L / (m?R?T); P1 = exp(lnP2 = L / m ?RT)
подставим значения величин и вычислим
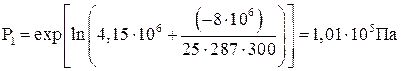
P1 = 0,101 МПа.
Начальный объем найдем из уравнения состояния
V1 = m?RT / P1 = 25 ? (287 ? 300) / 0,101 ? 106 = 21,3 м3.
Конечный объем найдем из соотношения между параметрами в изотермическом процессе.
V2 = P1 ? V1 / P2 = (0,101 ? 21,3) / 4,15 = 0,62 м3.
В изотермическом процессе теплота равна работе расширения
Q = L = -8 МДж.
Пример 1.7. В компрессор газотурбинной установки входят 5 кг воздуха с начальными параметрами: Р1 = 100 кПа и t1 = 27 0С. Воздух адиабатно сжимается до давления 400 кПа. Определить начальный и конечный объем, конечную температуру, работу сжатия и изменение внутренней энергии.
Решение: Начальный объем находим из уравнения состояния
V1 = m?RT1 / P1 = 5?287?800/(1?105) = 4,3 м3.
Конечный объем определяем из уравнения адиабаты
V2 = V1(P1 / P2)1/k = 4,3?(100/4000)1/1,4 = 0,262 м3.
k – показатель адиабаты для двухатомного газа, k = 1,4.
Конечную температуру определили или из уравнения адиабаты или из уравнения состояния
T2 = P2?V2 / (m?R) = 4?106 ? 0,262 / (5?287) = 720.
Находим работу сжатия L = (P1V1 – P2V2)/(k - 1) = (0,1?106?4,3 –
- 4?106?0,262) ?103/(1,4 - 1) = - 1550 кДж..
Изменение внутренней энергии вычисляем из 1-го закона термодинамики для адиабатного процесса
ΔU = - L = 1550 кДж.
Пример 1.8. 2 кг воздуха с начальной температурой t1 = 17 0C и давлением Р1 = 0,2 МПа сжимаются по политропе с уменьшением объема в 5раз. Давление в конце сжатия Р2 = 1,62 МПа. Определить работу и теплоту в процессе, изменение внутренней энергии и энтропии. Изобразить процесс в PV- и TS- диаграммах состояния. Теплоемкость считать постоянной.
Решение:Найдем показатель политропы сжатия
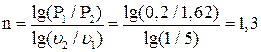
Температуру воздуха в конце сжатия определим, исходя из зависимости между параметрами состояния в политропном процессе
T2 = T1 (υ1 / υ2)n-1 = 290 ? 5(1,3 - 1) = 470 К.
Работа сжатия
L = mR(T1 – T2)/(n - 1) = 2?0,287(290 - 470)/(1,3-1) = - 344 кДж.
Количество теплоты
Q = mCn (T2 – T1) =2(-0,24)(470 - 290) = -84 кДж.
Cn – теплоемкость в политропном процессе
Cn = Cυ(n - k)/(n - 1)=μCυ(n - k)/M(n - 1) = 20,95(1,3 – 1,4)/29(1,3 - 1) =
= -0,24кДж/кг?К.
Изменение внутренней энергии
ΔU = Cυ(T2 – T1) = 20,95(470 - 290) = 130 кДж/кг.
Изменение энтропии
ΔS = Cnln(T2/T1) = -0,24ln(470/290) = -0,116 кДж/(кг?К).
Примерный вид процесса в PV- и TS- координатах показан на рис.3.

Рис.3. Изображение политропного процесса (пример 1.8) в Рυ –и TS – диаграммах, 1-2 – политропный процесс с n = 1,3; 1-2? - адиабата; 1-2? - изотерма.
Дата добавления: 2017-04-20; просмотров: 8833;
