Процентные ставки и методы их начисления.

В продолжение обзора показателей, учитывающих временную ценность денежных вложений, необходимо обратить внимание на формулу Фишера, которая объединяет основные финансовые переменные:

§ реальную процентную ставку, не содержащую фактор инфляции (r);

§ номинальную процентную ставку, рассчитанную с учетом инфляции (rⁿ);

§ ожидаемую ставку инфляции (h).

Зависимость между процентными ставками и ожидаемой инфляцией может быть представлена следующим выражением:

(1 + rⁿ) = (1 + r)∙(1 + h).

Из данной зависимости номинальная процентная ставка рассчитывается по формуле:

rⁿ = r + i + r∙h.

В условиях низкой инфляции на практике пренебрегают значением (r∙h), используя при этом упрощенную формулу расчета номинальной процентной ставки rⁿ = r+h.

В качестве информационной базы инвестиционного анализа часто используются исторические данные и материалы, собранные на основе текущей информации. Очевидно, что если базовые переменные в будущих периодах времени изменят свои предполагаемые значения, то соответственно произойдет изменение ожидаемой эффективности инвестиционных операций. Таким образом, можно сделать следующие выводы:

1. Цена заемного капитала уже включает ожидаемую инфляцию.

2. Заемщики капитала будут в наибольшей выгоде, если фактический уровень инфляции больше, чем ожидаемый рост цен, и соответственно планируемая ими эффективность от проведения финансово- инвестиционных операций будет значительно ниже, если фактическая инфляция ниже ее ожидаемого уровня.

3. Величина реальной процентной ставки воздействует на результативность осуществления финансовых операций. Чем выше значение r, тем ниже текущая стоимость получаемых в будущем доходов (процентов, дивидендов и пр.), и, наоборот, чем ниже значение r, тем большую ценность имеют будущие результаты с позиции их текущей стоимости. Осуществление инвестиционного анализа неразрывно связано с учетом временных параметров реализации долговременных капиталовложений. В связи с этим процедуры анализа проектной дисконтной ставки выступают в качестве базовых мероприятий, осуществление которых во многом предопределяет степень объективности результатов оценки эффективности долгосрочных инвестиций.

В финансовых расчетах с использованием сложных процентов принято определять эффективную ставку, т.е. такую годовую номинальную ставку сложных процентов, которая дает возможность получить тот же результат, как и при начислении процентов несколько раз в году. Равенство наращенных сумм обеспечивается здесь равенством первоначальных сумм, периодов и множителей наращения.

Эффективная процентная ставка будет больше номинальной. Это видно из соответствующих алгоритмов, где r_эф - эффективная ставка. Множители наращения должны быть равны:

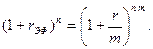
Отсюда эффективная ставка составит:

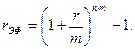
Используя приведенный алгоритм, рассчитаем эффективную ставку сложных процентов при ежеквартальном начислении, если номинальная ставка - 15%, а период равен году. Первоначальная сумма - 500 тыс. руб.

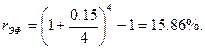
Наращенная сумма при этом составит:

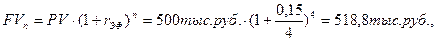
При начислении сложных процентов четыре раза в году получим ту же наращенную сумму:

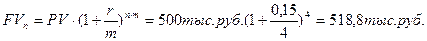
Две или несколько приведенных сумм денег считаются эквивалентными, если их современные ценности одинаковы. Эквивалентность приведенных сумм используется для сравнения контрактов на получение ссуды, а также при решении вопроса об изменении условий такого рода сделки.

Пример. В первом контракте сумма обязательства состаатяет 20 000 руб. исходя из простых 30% в год с выплатой 12 000 руб. через два года, остальных 8000 руб. - через пять лет, т.е. по окончании контракта.

Во втором контракте сроком на четыре года под тот же простой процент возврат первой части обязательства в сумме 7000 руб. предусмотрен через год, а остальной суммы - через три года от настоящего момента.

Надо рассчитать сумму долга во втором контракте, которая будет возвращена через три года, при условии, что современные ценности потоков платежей в обоих контрактах будут одинаковыми, эквивалентными, т.е.:

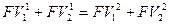
где 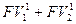- дисконтированные (приведенные) суммы платежей в первом контракте;

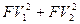- дисконтированные (приведенные) суммы платежей во втором контракте.

В качестве наращенной суммы (FV) принимается сумма обязательства вернуть долг, включая проценты. Тогда приведенная к настоящему моменту сумма обязательного платежа составит:

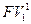= 12000 : (1+0,3×2) = 7500 руб.

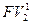= 8000 : (1+0,3×5) = 3200 руб.

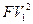= 7000 : (1+0,3×1) = 5384,6 руб.

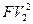= 12000 : (1+0,3×3) = Х руб. : 1,9.

Контракты будут эквивалентны, если будет выполнено равенство:

7500 руб. + 3200 руб. = 5384,6 руб. + X руб. : 1,9.

Отсюда X руб. = (7500 + 3200 - 5384,6) х 1,9 = 10099,3 руб.

Из примера видно, что сокращение срока платежа во втором контракте, позволяет уменьшить суммарные выплаты. По первому контракту они составят 20000 руб. (12000 + 8000), а по второму - 17099,3 руб. (7000 + 10099,3).

На практике финансовые операции обычно совершаются с использованием сложных процентов. Кредитные взаимоотношения, осуществление долгосрочных финансово-кредитных операций, оценка инвестиционных проектов нередко требуют применения математических моделей непрерывного начисления процентов, их реинвестирования, использования сложных процентов. Особенность процесса при этом состоит в том, что исходная базовая сумма увеличивается с каждым периодом начисления, в то время как при использовании простых процентов она остается неизменной. Наращение по сложным процентам осуществляется с ускорением. Процесс присоединения начисленных процентов к базовой сумме носит название капитализации процентов.

Чаще всего финансовые операции имеют продолжительный характер, состоят не из одного разового платежа, а из потоков платежей и нередко с разными знаками. В качестве примера можно привести: ежегодные выплаты процентов по облигациям, ежемесячные взносы на погашение потребительского кредита, получение ежемесячных стипендий от благотворительного фонда; арендные платежи; периодические вклады в банк для образования страхового фонда и др.

В таких финансовых операциях возникает необходимость найти наращенную сумму потока платежей или, наоборот, по наращенной сумме определить величину отдельного платежа. Для целого ряда финансовых расчетов разработаны математические модели, которые можно найти в специальной литературе.