Операции наращения и дисконтирования.
Концепция стоимости денег во времени.
Временная ценность денежных вложений относится к одной из основных концепций, используемых в инвестиционном анализе. Необходимость учета временного фактора заставляет особое внимание уделять оценке базовых финансовых показателей. Разность в оценке текущих денежных средств и той же самой их суммы в будущем может быть связана с:
§ негативным воздействием инфляции, в связи с чем происходит уменьшение покупательной способности денег;
§ возможностью альтернативного вложения денежных средств и их реинвестирования в будущем (фактор упущенной выгоды);
§ ростом риска, связанного с вероятностью невозврата инвестированных средств (чем длительнее срок вложения капитала, тем выше степень риска);
§ потребительскими предпочтениями (лучше получить меньше доход в ближайшем периоде, чем ожидать большее, но в отдаленной перспективе).
В планируемом периоде анализ предстоящей реализации различного вида инвестиционных проектов может осуществляться по двум противоположным направлениям. С одной стороны, определяется будущая стоимостная оценка первоначальной величины инвестиций и доходов (дивидендов, процентов, прибыли, денежных потоков и пр.), полученных в результате осуществления этих капиталовложений. С другой стороны, приращенные в ходе инвестирования денежные средства оцениваются с позиции их текущей (настоящей) стоимости. В соответствии с этим в финансово-инвестиционном анализе используются операции дисконтирования и наращения капитала. Принципиальная схема инвестиционного анализа, осуществляемого с учетом временной ценности денежных вложений, представлена на рис. 1.

Рис. 1. Схема проведения инвестиционного анализа с использованием операций наращения и дисконтирования капитала
Операции наращения и дисконтирования.
При разработке оптимальных финансовых решений в определенных ситуациях требуется проведение оценки будущей стоимости инвестированных денежных средств. Нахождение будущей стоимости денежных средств по истечении одного периода времени и при известном значении темпа их прироста осуществляется по формуле
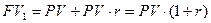

где FV1- будущая стоимость денежных средств в конце первого периода инвестирования (t=1), тыс. руб.;
РV - первоначальная (принципиальная) сумма денежных средств, инвестированных в начальный период времени (t = 0), тыс. руб.;
r - темп прироста денежных средств, коэф.
Процесс, в котором при заданных значениях PV и r необходимо найти величину будущей стоимости инвестированных средств к концу определенного периода времени (n) называется операцией наращения. В практике инвестиционного анализа «темп прироста» денежных средств принято называть «процентом», «ставкой процента» или «нормой рентабельности», а первоначальную сумму денежных средств - «текущей стоимостью» (РV).
Из предыдущей зависимости FV1 от РV темп прироста денежных средств исчисляется по формуле:
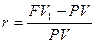
Оценка будущей стоимости денежных вложений, инвестированных на срок более одного периода времени, - более сложная задача. Ответ на вопрос, какой будет будущая стоимость денежных средств в n-й период времени, зависит от того, простой или сложный процент будет применяться в расчетах. Использование простого процента (simple interest) свидетельствует о том, что инвестор будет получать доход (наращивать капитал) только с принципиальной суммы начальных инвестиций в течение всего срока реализации проекта. В противоположность данному подходу использование сложного процента (compound interest) говорит о том, что полученный доход (проценты, дивиденды или пр.) периодически добавляется к сумме начальной инвестиции, в результате помимо первоначальной суммы денежных средств процент берется также из накопленной в предыдущих периодах суммы процентных платежей или любого другого вида доходов. В математическом исчислении операция наращения с использованием сложных процентов к концу второго периода реализации проекта определяется по формуле
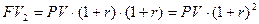
В конце n-гo периода времени будущая стоимость денежных средств (FVn) исчисляется по формуле:
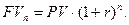
Данная формула расчета FVn является базовой в инвестиционном анализе. Для облегчения процедуры нахождения показателя FVn предварительно рассчитывается величина множителя (1+r)n при различных значениях r и n. В этом случае FVn находим по формуле:
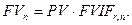
где FVIFr,n - фактор (множитель) будущей стоимости денежных вложений, коэф.
В инвестиционном анализе под стандартным временным интервалом принято рассматривать один год. В случае же, когда дополнительно оговаривается частота выплаты процентов по вложенным средствам в течение года, формула расчета будущей стоимости инвестированного капитала может быть представлена в следующем виде:
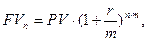
где r - годовая процентная ставка, коэф.;
m - количество начислений в году, ед.;
n - срок вложения денежных средств, год.
Начисление процентов (дивидендов или др.) может осуществляться ежедневно, ежемесячно, поквартально, один раз в полугодие и один раз в год. Характерно, что чем больше количество раз в течение года будут начисляться проценты, тем больше будет FV в конце n-го периода времени. Для целей анализа отношение r/m принято рассматривать в качестве процентной ставки, а произведение - n∙m в качестве срока инвестирования. Этот случай соответствует следующей экономической ситуации.
Пример. Коммерческая организация приняла решение инвестировать на пятилетний срок свободные денежные средства в размере 30 тыс. руб. Имеются три альтернативных варианта вложений. По первому варианту средства вносятся на депозитный счет банка с ежегодным начислением сложных процентов по ставке 20 % годовых. По второму варианту средства передаются сторонней организации в качестве займа, при этом на переданную в долг сумму ежегодно начисляется 25 %. По третьему варианту средства помещаются на депозитный счет коммерческого банка с начислением сложных процентов по ставке 16 % годовых ежеквартально. Если не учитывать уровень риска, наилучший вариант вложения денежных средств может быть определен при помощи показателя FVn. По варианту I: FVn = 30 тыс. руб. × (1+0,2)5 = 74,7 тыс. руб. По варианту II: FVn = 30 тыс. руб. + 5 × (30 тыс. руб. × 0,25) = 67,5 тыс. руб. По варианту III: FVn - 30 тыс. руб. × (1+0,16/4)5∙4 = 65,7 тыс. руб. В данных условиях первый вариант более предпочтителен для предприятия.
Наращение денежных средств имеет максимальное (предельное) значение, когда интервал наращения становится бесконечно малым (количество начислений в году стремится к бесконечности). В этом случае показатель FVn определяется по формуле:
FVn = PV∙er∙n
где е - трансцендентное число е, равное 2,718281...(постоянная величина).
В финансовых расчетах должна учитываться инфляция, тем более если она значительна. С одной стороны, сумма, положенная, например, на депозит, получит приращение, а с другой - утратит свою реальную стоимость в результате инфляции. Для определения наращенной суммы с учетом инфляции используют алгоритм:
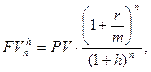
где 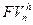 - будущая стоимость денежных средств c учетом инфляции в конце n-ого периода инвестирования, тыс. руб.;
- будущая стоимость денежных средств c учетом инфляции в конце n-ого периода инвестирования, тыс. руб.;
РV - первоначальная (принципиальная) сумма денежных средств, инвестированных в начальный период времени, тыс. руб.;
r - темп прироста денежных средств, коэф.
m - число начислений в году;
h - ожидаемый месячный темп инфляции;
n - число месяцев.
Пример. Предположим, что на депозит положена сумма 1000 тыс. руб. Номинальная годовая банковская ставка равна 16%. Сложные проценты начисляются каждый месяц, т.е. годовая номинальная ставка применяется 12 раз в году (m). Ожидаемый месячный темп инфляции равен 10%. Определим наращенную сумму (с учетом инфляции) через 5 месяцев, а также эрозию капитала (ЭК), или уменьшение реальной стоимости суммы, положенной на депозит 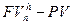 :
:
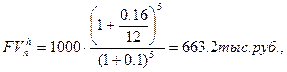
Эрозия капитала составит: 663,2 тыс. руб. - 1000 тыс. руб. = - 336,8 тыс. руб.
Как и в случае с наращением капитала, для оптимального принятия финансовых решений чрезвычайно важно знать и учитывать в анализе временной интервал дисконтирования. Если начисление процентов планируется (или произошло) более одного раза в год, формулу для нахождения РV необходимо представлять в следующем виде:
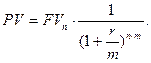
Возможности практического использования показателя PV pacкрываются в различных экономических ситуациях, когда возникает необходимость обоснования финансово-инвестиционных решений с учетом временной ценности денежных вложений.
Одна из типичных ситуаций в инвестиционной деятельности хозяйствующих субъектов представлена ниже.
Пример. Коммерческая организация планирует приобрести помещения под склад и офис. Эксперты оценивают будущую стоимость недвижимости в размере 10 млн. руб. По банковским депозитным счетам установлены ставки в размере 18% с ежегодным начислением сложных процентов и 14% с ежеквартальным начислением сложных процентов. При помощи показателя PV можно определить, какую сумму средств необходимо поместить на банковский депозитный счет, чтобы через два года получить достаточную сумму для покупки недвижимости. Расчет оптимального варианта инвестирования осуществляется следующим образом: в первом случае PV = 10 млн руб. × (1/[1 + 0,18]2) = 7,18 млн руб.; во втором случае РV = 10 млн. руб.∙(1/[1 +0,14/4]2×4) = 7,59 млн руб. Очевидно, что более выгодным для предприятия является вложение меньшей суммы средств, т.е. первый вариант.
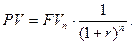
Отношение 1/(1+r)n известно как фактор (множитель) текущей стоимости (РVIFr,n). Стандартные значения РVIFr,n могут быть найдены в специальных таблицах. Формула расчета PV уравнивает, с точки зрения инвестора, ценность денежных средств сегодня и ожидаемого к получению денежного потока в будущем.
При заданной величине дисконтной ставки текущая стоимость денежных потоков достигнет своего минимально возможного значения при непрерывном дисконтировании. В этом случае (когда m => +∞) текущая стоимость исчисляется по формуле:
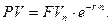
Дата добавления: 2017-04-20; просмотров: 1092;
