Показатели изменения уровней рядов динамики.
Базисные показатели - уровень данного периода сравнивается с первым (базисным) периодом.
Цепные показатели – сравниваются уровни двух соседних периодов.
1) абсолютное изменение (∆y) (абсолютный прирост) – показывает, на сколько, в абсолютном изменении, уровни исследуемых периодов больше (или меньше), чем уровень базисного периода (базисный абсолютный прирост ∆yб) или, чем уровень соседнего периода (цепной абсолютный прирост ∆yц):
∆yб= yn – y1и∆yц = yn – yn-1
Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени, т.е. ∑∆yц = ∆yб
Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уровень по сравнению с предыдущим в среднем за единицу времени. Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня и всегда является интервальным показателем. Он вычисляется путем деления общего прироста за весь период на длину этого периода в тех или иных единицах времени:
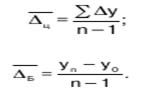
2) относительное изменение (Тр) (темп роста или индекс динамики) показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (Тр>1) или какую его часть составляет (Тр <1). Темп роста может выражаться в процентах.
Трб = yn / y1 и Трц = yn / yn-1
Средний темп роста рассчитывается по простой средней геометрической.
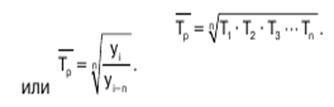
3) темп изменения (Тпр) (темп прироста) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения.
Тпр = Тр - 1,0илиТпр = Тр – 100%
Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, которая имеет место между обычными темпами роста и прироста:
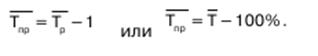
Средний темп прироста (или снижения), выраженный в процентах, показывает, на сколько процентов увеличивался (или снижался) уровень по сравнению с предыдущим в среднем за единицу времени. Средний темп прироста характеризует среднюю интенсивность роста.
Пример:
Число жителей России в 2004-2009 гг. в млн.чел, на 1 января
| Год | y | ∆yб | ∆yц | Трб | Трц | Тпрб,% | Тпрц, % |
| 144,2 | |||||||
| 143,5 | -0,7 | -0,7 | 0,995 | 0,995 | -0,49 | -0,49 | |
| 142,8 | -1,4 | -0,7 | 0,990 | 0,995 | -0,97 | -0,49 | |
| 142,2 | -2,0 | -0,6 | 0,986 | 0,996 | -1,39 | -0,42 | |
| 142,0 | -2,2 | -0,2 | 0,985 | 0,999 | -1,53 | -0,14 | |
| 141,9 | -2,3 | -0,1 | 0,984 | 0,999 | -1,60 | -0,07 | |
| Итого | - | - | -2,3 | - | 0,984 | - | -1,60 |
Дата добавления: 2017-04-20; просмотров: 783;
