Аналитическое сравнение ФМ и ЧМ.
Полученные результаты для наглядности сведем в таблицу. Сопоставляя выражения таблицы 1, легко установить различие между ФМ в ЧМ и обратно ЧМ в ФМ.
Таблица 1.
| ЧМ | ФМ |
Определение:
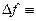 UF (1)
Девиация фазы: UF (1)
Девиация фазы:
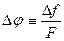 (3) (3)
| Определение:
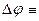 UF (2)
Девиация частоты: UF (2)
Девиация частоты:
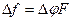 (4) (4)
|
Как видно, при ФМ девиация фазы зависит от амплитуды модулирующего напряжения, но зато девиация частоты зависит от обоих параметров модулирующего сигнала, т.е. от его амплитуды и частоты. При ЧМ, наоборот, девиация частоты зависит только от амплитуды, но зато девиация фазы зависит как от амплитуды, так и от частоты модулирующего напряжения.
Если в выражении (2.14) зафиксировать F, то останется только прямая пропорциональность 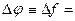 UF , т.е. получим ФМ.
UF , т.е. получим ФМ.
Если в выражении (2.13) зафиксировать F, то 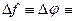 UF, т.е. получим ЧМ. Следовательно, при модуляции одним тоном нельзя установить примененный вид модуляции; ФМ и ЧМ в этом случае тождественны.
UF, т.е. получим ЧМ. Следовательно, при модуляции одним тоном нельзя установить примененный вид модуляции; ФМ и ЧМ в этом случае тождественны.
Максимальную девиацию фазы при ФМ называют индексом фазовой модуляции
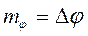 .
.
Амплитуду девиации фазы при ЧМ называют также индексом частотной модуляции М:
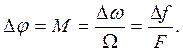
Методы превращения ФМ в ЧМ и ЧМ в ФМ вытекают из сопоставления накрест лежащих выражений в таблице 1. Формула (4) показывает фактическую зависимость, а формула (1) – требуемую для превращения ФМ в ЧМ. Аналогично для получения ФМ из ЧМ следует формулу (3) превратить в (2).
Для простоты математических преобразований предположим, что модулирующий сигнал изменяется по закону синусоиды при ФМ и по закону косинусоиды – при ЧМ.
Имеем выражение для текущего значения фазы при ФМ
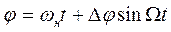 (2.7)
(2.7)
и для текущего значения частоты при ЧМ
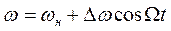 (2.8)
(2.8)
Определим закон изменения частоты при ФМ и фазы при ЧМ. Текущее значение частоты при ФМ получается равным
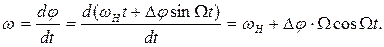 (2.9)
(2.9)
Выражение перед косинусом представляет собой амплитуду девиации частоты при ФМ
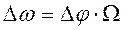 (2.10)
(2.10)
Текущее значение фазы при ЧМ
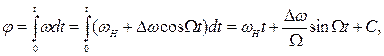 (2.11)
(2.11)
где 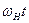 -основная фаза;
-основная фаза;
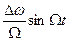 -дополнительная фаза, появившаяся в результате модуляции;
-дополнительная фаза, появившаяся в результате модуляции;
С – постоянная интегрирования; С= 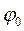 , принимаем
, принимаем 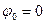 .
.
В формуле (2.11) выражение перед синусом является амплитудой девиации фазы при ЧМ:
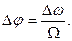 (2.12)
(2.12)
Наибольший интерес представляют выражения (2.10) и (2.12). Переходя в них к циклическим частотам, получим:
амплитуда девиации частоты при ФМ
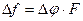 ; (2.13)
; (2.13)
амплитуда девиации фазы при ЧМ
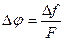 (2.14)
(2.14)
Выражение для мгновенного значения амплитуды ЧМ(ФМ) сигнала при модуляции одним тоном выглядит следующим образом:
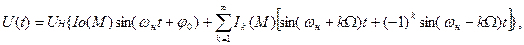 (2.15)
(2.15)
где Uн – амплитуда ВЧ сигнала без модуляции (М=0);
Iк (М) – функции Бесселя порядка К от аргумента равного индексу модуляции М.
Из выражения (2.15) следует, что спектр симметричен (к = 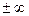 ); имеет линейную структуру (соседние составляющие отстают друг от друга на одну и туже величину
); имеет линейную структуру (соседние составляющие отстают друг от друга на одну и туже величину 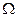 ); амплитуды составляющих спектра определяются функцией Бесселя.
); амплитуды составляющих спектра определяются функцией Бесселя.
Теоретически спектр ЧМ колебания бесконечно широк, но, учитывая монотонное убывание боковых, его можно ограничивать в пределах полосы, определяемой как:
Пчм=2F (1+M+ 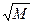 ). (2.16)
). (2.16)
Для радиовещательных РПДУ с ЧМ максимальная девиация частоты установлена 50 Гц и верхняя граница спектра звукового сигнала F=15 кГц. При этом индекс частотной модуляции М= 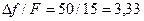 .Тогда требуемая полоса пропускания составит около 180 кГц, что в шесть раз больше аналогичного параметра при АМ (Пам=2Fмакс). Это обстоятельство заставляет использовать ЧМ(ФМ) только в таких ёмких диапазонах, как УКВ, ДМВ и СМВ.
.Тогда требуемая полоса пропускания составит около 180 кГц, что в шесть раз больше аналогичного параметра при АМ (Пам=2Fмакс). Это обстоятельство заставляет использовать ЧМ(ФМ) только в таких ёмких диапазонах, как УКВ, ДМВ и СМВ.
В системах низовой радиосвязи часто применяют узкополосную ЧМ, имеющую индекс модуляции М 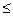 1 и
1 и 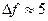 кГц. По своей спектральной характеристики и помехозащищенности она практически не отличается от АМ.
кГц. По своей спектральной характеристики и помехозащищенности она практически не отличается от АМ.
Дата добавления: 2016-02-04; просмотров: 3827;
