Замкнутой САУ называют систему, в которой процесс управления ОУ зависит от результата управления. 5 страница
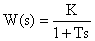
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как
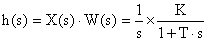 .
.
Корни характеристического уравнения  определяются как
определяются как
 .
.
Выполняя обратное преобразование изображения переходной характеристики 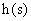 получаем:
получаем:
 .
.
Выполняя аналогичные преобразования над изображением весовой функции

получаем выражение для определения весовой функции 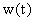 .
.
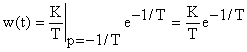
Переходная и весовая характеристики звена приведены на рис. 5.
T 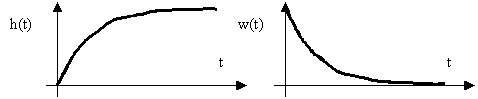
Рис. 5. Временные характеристики апериодического звена.
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:
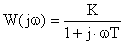
Исходя из этого, амплитудно-частотная характеристика звена определяется как:
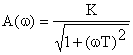 .
.
Вещественная  и мнимая
и мнимая  частотные характеристики звена определяются как
частотные характеристики звена определяются как

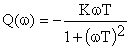
АФЧХ звена определяется как
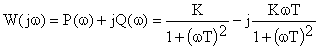
Выражение для расчета ЛАЧХ принимает вид:
 .
.
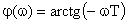 .
.
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
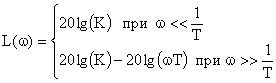 .
.
На рис. 6 приведены амплитудно-фазовая и логарифмическая частотные характеристики безинерционного звена.
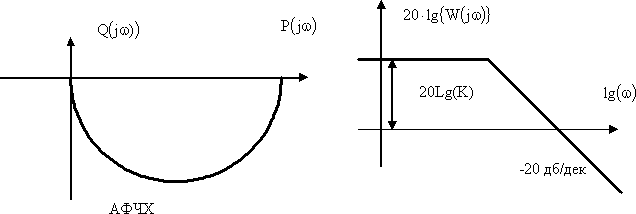
Рис. 6. Амплитудно-фазовая частотная и логарифмическая частотные характеристики апериодического звена
5.2.3. Интегрирующее звено
Уравнение движения для интегрирующего звена имеет вид
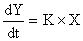
Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:

Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Переходная характеристика звена определяется как
 .
.
Весовая характеристика определяется как
 .
.
Эти характеристики интегрирующего звена приведены на рис. 7.
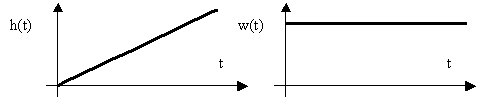
Рис. 7. Временные характеристики интегрирующего звена
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:

Исходя из этого, амплитудно-частотная характеристика звена определяется как:
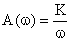
Вещественная  и мнимая
и мнимая  частотные характеристики звена определяются как
частотные характеристики звена определяются как
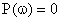 .
.
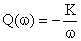
Выражение для расчета ЛАЧХ принимает вид:
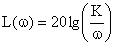

Рис. 8. Амплитудно-фазовая частотная и логарифмическая частотные характеристики звена.
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
 .
.
Амплитудно-фазовая и логарифмическая частотные характеристики звена показаны на рис. 8.
5.2.4. Дифференцирующее звено
Уравнение движения для дифференцирующего звена имеет вид
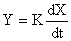
Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:
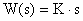
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Переходная характеристика дифференцирующего звена определяется как
 .
.
На рис. 9. приведена переходная характеристика дифференцирующего звена.
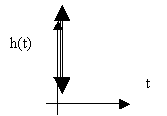
Рис. 9. Переходная характеристики звена
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:
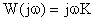
Исходя из этого, амплитудно-частотная характеристика звена определяется как:
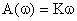
Вещественная  и мнимая
и мнимая  частотные характеристики звена определяются как
частотные характеристики звена определяются как
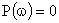 .
.


Рис. 10. Амплитудно-фазовая частотная и логарифмическая частотные характеристики звена
Выражение для расчета ЛАЧХ принимает вид:
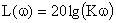
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
 .
.
Амплитудно-фазовая и логарифмическая частотные характеристики звена показаны на рис. 10.
5.2.5. Колебательное звено
Уравнение движения для колебательного звена имеет вид
 ,
,
где 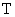 – постоянная времени звена,
– постоянная времени звена,
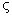 — коэффициент демпфирования.
— коэффициент демпфирования.
Выполняя над этим уравнением преобразование Лапласа, получаем выражение для передаточной функции звена следующего вида:

Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Корни характеристического уравнения звена определяются как:

Для колебательного звена характерно различное распределение корней при разных комбинациях его параметров. В общем случае выражение переходная характеристика определяется выражением вида:
 ,
,
где  — декремент затухания;
— декремент затухания;
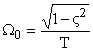 — частота собственных колебаний;
— частота собственных колебаний;
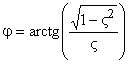 — начальная фаза колебаний
— начальная фаза колебаний
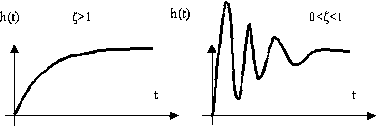
Рис. 11. Временные характеристики звена
Временные характеристики колебательного звена определяются распределением корней его характеристического полинома. На рис. 11 приведены переходные характеристики колебательного звена при действительно и комплексно-сопряженных корней характеристического полинома.
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:
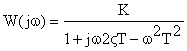
Исходя из этого, амплитудно-частотная характеристика колебательного звена определяется как:
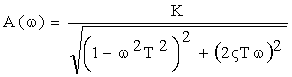
Вещественная  и мнимая
и мнимая  частотные характеристики звена определяются как
частотные характеристики звена определяются как
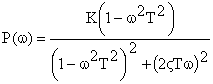 .
.

Выражение для расчета ЛАЧХ принимает вид:
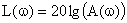
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
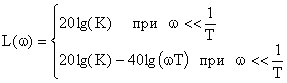 .
.
Амплитудно-фазовая и логарифмическая частотные характеристики звена показаны на рис. 12.
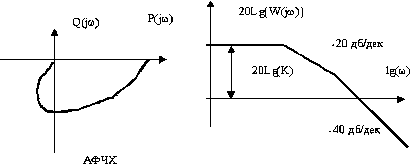
Рис. 12. Амплитудно-фазовая частотная и логарифмическая частотные характеристики колебательного звена
5.3. Правила структурных преобразований САУ и определение передаточных функций сложных систем.
Правила преобразования структурных схем, состоящих из отдельных динамических звеньев такие же, как при анализе статических характеристик САУ.
При параллельном соединении N звеньев передаточная функция САУ определяется как
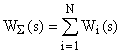 .
.
При параллельном соединении N звеньев передаточная функция САУ определяется как
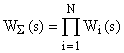 .
.
При охвате звена с передаточной функцией 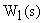 W звеном, передаточная функция которого
W звеном, передаточная функция которого 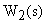 , передаточная функция САУ определяется как:
, передаточная функция САУ определяется как:
 .
.
При исследовании САУ структурные схемы используются для определения ее передаточной функции. Эта задача не представляет труда для относительно простых систем, для которых возможно упрощение структурной схемы на основе тех же правил, которые используются при анализе статических характеристик САУ. В ряде случаев для определения передаточных функций систем со сложными перекрестными связями оказывается полезным применение правила Мезона (Мейсона). Согласно этому правилу передаточная функция, связывающая две координаты САУ, определяется как
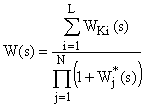 ,
,
где 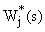 — передаточная функция j-го замкнутого контура, входящего в состав рассматриваемой САУ,
— передаточная функция j-го замкнутого контура, входящего в состав рассматриваемой САУ, 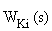 — передаточная функция, связывающая рассматриваемые координаты, L – число путей, связывающих рассматриваемые координаты САУ, N – число локальных замкнутых контуров, входящих в состав рассматриваемой САУ.
— передаточная функция, связывающая рассматриваемые координаты, L – число путей, связывающих рассматриваемые координаты САУ, N – число локальных замкнутых контуров, входящих в состав рассматриваемой САУ.
В числителе выражения для определения передаточной функции сложной САУ записывается сумма всех прямых путей, связывающих рассматриваемые координаты. Символ 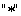 в знаменателе приведенного выражения указывает, что рассматриваются только взаимонесвязанные, то есть не имеющие общих элементов, замкнутые локальные контуры САУ.
в знаменателе приведенного выражения указывает, что рассматриваются только взаимонесвязанные, то есть не имеющие общих элементов, замкнутые локальные контуры САУ.
Однако для сложных систем автоматического управления с большим числом взаимосвязанных переменных составление структурной схемы сопряжено с большими трудностями и может быть проведено только на основании детального анализа исходных дифференциальных уравнений САУ. В этом случае применение метода структурных схем не облегчает нахождения основных уравнений системы. Однако при дальнейшем исследовании САУ структурная схема может оказаться полезной, так как в ней наглядно представлены все узлы системы и существующие между ними связи.
Большинство САУ представляют собой многоконтурные структуры. Методы же анализа и синтеза разработаны для одноконтурных систем. В связи с этим возникают проблемы приведения исходной системы к одноконтурной. Для этого используется несколько правил.
Правила переноса точки отвода обратной связи.
При переносе точек отвода обратной связи необходимо сохранять равенство передаточных коэффициентов. Рассмотрим случай переноса точки отвода обратной связи по направлению прохождения информации. Исходная и преобразованная структурная схемы САУ приведены на рис. 13. Для сохранения равенства передаточных коэффициентов обеих систем вводится звено, коэффициент передачи которого равен В.

Рис. 13. Перенос обратной связи по направлению передачи информации.
Передаточный коэффициент исходной системы
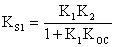
Передаточной коэффициент преобразованной системы:
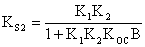
При  имеем, что
имеем, что
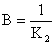 .
.
Таким образом, при переносе точки обратной связи по направлению прохождения информации, дополнительный элемент должен иметь передаточный коэффициент обратный 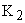 .
.
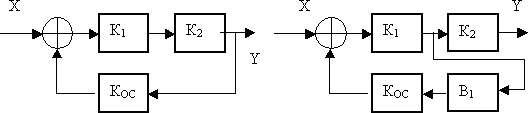
Рис. 14. Перенос точек отвода обратной связи против направления передачи информации.
Для анализа случая переноса точки отвода обратной связи против направления прохождения информации рассмотрим исходную и преобразованную структурные схемы САУ. Они приведены на рис. 14. Для сохранения равенства передаточных коэффициентов обеих систем вводится звено, коэффициент передачи которого равен 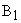 .
.
Передаточный коэффициент исходной системы
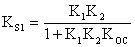
Передаточной коэффициент преобразованной системы:
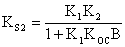
При  имеем, что
имеем, что
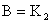 .
.
Таким образом, при переносе точки обратной связи против направления прохождения информации, дополнительный элемент должен иметь передаточный коэффициент, равный 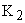 .
.
Другой важной операцией преобразования структурных схем является перенос сумматора. При переносе сумматора по направлению переноса информации (рис. 15) необходимо добавить звено с передаточным коэффициентом, равным коэффициенту передачи звена, через которое переносится сумматор.
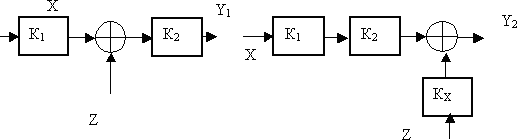
Рис. 15. Перенос сумматора по направлению прохождения информации
Справедливость этого утверждения следует из следующих преобразований. Сигнал на выходе исходной САУ определяется как
 .
.
Сигнал на выходе САУ после проведения структурных преобразований определяется как
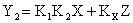
При равенстве сигналов на выходе исходной и преобразованной структурных схем САУ, то есть при выполнении условия 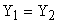 . Для выполнения этого условия необходимо выполнение условия, определяемого решением уравнения вида:
. Для выполнения этого условия необходимо выполнение условия, определяемого решением уравнения вида:
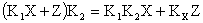
Решением этого уравнения получаем, что
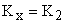 .
.
При переносе сумматора против направления прохождения информации рассмотрим исходную и преобразованную структурные схемы САУ, представленные на рис. 16.
В этом случае сигнал на выходе исходной САУ определяется как
 .
.
Сигнал на выходе САУ после проведения структурных преобразований определяется как
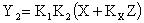 .
.

Рис. 16. Перенос сумматора по направлению прохождения информации
При равенстве сигналов на выходе исходной и преобразованной структурных схем САУ, то есть при выполнении условия 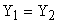 . Для выполнения этого условия необходимо выполнение условия, определяемого решением уравнения вида:
. Для выполнения этого условия необходимо выполнение условия, определяемого решением уравнения вида:
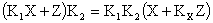
Решением этого уравнения получаем, что
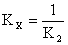 .
.
То есть при переносе сумматора против направления прохождения информации необходимо добавлять звено с передаточным коэффициентом, равным обратному передаточному коэффициенту звена или звеньев, через которые переносится сумматор.
Вопросы.
1. Что называется элементарным динамическим звеном?
2. Как определяется порядок элементарного звена или САУ?
3. Какие характеристики используются для сравнения элементарных звеньев?
4. Какими особенностями характеризуется безинерционное звено?
5. Как определяется импульсная переходная характеристика динамического звена?
6. Какими особенностями характеризуется интегрирующее звено?
7. Какими особенностями характеризуется дифференцирующее звено?
8. Как определить коэффициент усиления интегрирующего звена?
9. Какими особенностями характеризуется апериодическое звено?
10. Какими особенностями характеризуется колебательное звено?
11. Как определяется постоянная времени элементарного звена?
12. Что характеризует постоянная времени элементарного звена?
13. Как построить асимптотическую логарифмическую частотную характеристику колебательного звена?
14. Как изменяются свойства колебательного звена при изменении коэффициента демпфирования?
15. Что называется добротностью интегрирующего звена?
16. Как определяется переходная характеристика элементарного звена?
17. Что называется 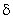 — функцией?
— функцией?
18. Как определить передаточную функцию САУ, состоящей из нескольких последовательно соединенных динамических звеньев?
19. Как определить передаточную функцию САУ, состоящей из нескольких параллельно соединенных динамических звеньев?
20. Как определяется передаточная функция САУ с отрицательной обратной связью?
21. Какие правила используются при переносе сумматора в структурной схеме САУ?
22. Как используется правило Мезона для определения передаточной функции САУ? Показать на конкретном примере.
Тема 6. Характеристики основных элементов САУ.
1. Усилители мощности
1.1. Тиристорный преобразователь.
Тиристорный преобразователь, как элемент САУ, представляет собой импульсную систему (СИФУ и выпрямитель ВП), преобразующую входной управляющий сигнал (напряжение 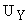 ) в функцию моментов отпирания тиристоров, изменяющую напряжение на входе двигателя
) в функцию моментов отпирания тиристоров, изменяющую напряжение на входе двигателя 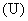 , и описываемую дифференциальным уравнением:
, и описываемую дифференциальным уравнением:
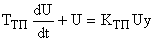 , ,
| (1) |
где 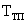 – постоянная времени тиристорного преобразователя (
– постоянная времени тиристорного преобразователя ( 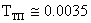 сек для мостовой полностью управляемой схемы);
сек для мостовой полностью управляемой схемы);
 – передаточный коэффициент тиристорного преобразователя
– передаточный коэффициент тиристорного преобразователя  .
.
При изменении напряжения управления на некоторую величину 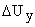 изменяется напряжение на входе двигателя
изменяется напряжение на входе двигателя  . Тогда уравнение (1) примет вид:
. Тогда уравнение (1) примет вид:
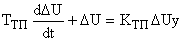
Переходя к операторной форме записи, получаем:
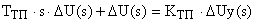
Отсюда выражение для передаточной функции тиристорного преобразователя принимает вид:
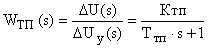
1.2. Широтно-импульсный преобразователь.
Широтно-импульсный преобразователь (ШИП) представляет набор электронных ключей, обеспечивающих импульсное изменение напряжения на нагрузке, подключенной к выходу этого преобразователя. В современной технике частоты коммутации ШИП лежат в пределах (2—50) кГц. Поэтому запаздывание в такой системе принимается равным нулю. Во многих приложениях ШИП представляется как безинерционный элемент с передаточной функцией 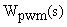 вида:
вида:
 ,
,
где  ,
, 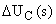 – величины приращений изображений выходного и входного сигнала ШИП соответственно.
– величины приращений изображений выходного и входного сигнала ШИП соответственно.
Более точное представление процессов в САУ, содержащей ШИП, может быть получено с использованием дискретного преобразования Лапласа.
2. Измерительные преобразователи и датчики.
2.1 Датчик тока
Датчик тока (измерительный трансформатор тока) с фильтром, как элемент САУ, описывается дифференциальным уравнением вида:
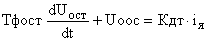 , ,
| (2) |
где  – передаточный коэффициент датчика тока;
– передаточный коэффициент датчика тока;
 – номинальный ток тиристорного преобразователя;
– номинальный ток тиристорного преобразователя;
 – постоянная времени фильтра в обратной связи по току.
– постоянная времени фильтра в обратной связи по току.
При изменении тока двигателя 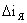 изменяется напряжение на выходе
изменяется напряжение на выходе  , тогда уравнение (2) в приращениях примет вид:
, тогда уравнение (2) в приращениях примет вид:
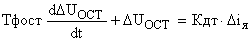 .
.
Это уравнение в операторной форме записи представляется как:
 .
.
Тогда передаточная функция датчика тока с фильтром примет вид:
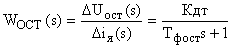 .
.
Для практических расчетов можно пренебречь постоянной времени фильтра ( 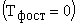 , тогда передаточная функция датчика тока примет вид безинерционного звена:
, тогда передаточная функция датчика тока примет вид безинерционного звена:
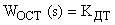 .
.
2.2. Датчики скорости
Наиболее широко применяемым в системах управления технологическим оборудованием датчиком скорости является тахогенератор, на выходе которого включается дополнительный фильтр. Эти элементы САУ, описываются следующим дифференциальным уравнением:
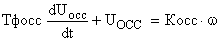 , ,
| (3) |
где 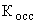 – коэффициент обратной связи по скорости;
– коэффициент обратной связи по скорости;
 – постоянная времени фильтра в обратной связи по скорости.
– постоянная времени фильтра в обратной связи по скорости.
Тахогенератор является безинерционным звеном  , а инерционность вносится за счет фильтра (
, а инерционность вносится за счет фильтра (  ). При изменении скорости тахогенератора на
). При изменении скорости тахогенератора на 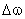 изменится и напряжение на выходе —
изменится и напряжение на выходе —  . Тогда уравнение (3) в приращениях примет вид:
. Тогда уравнение (3) в приращениях примет вид:
 ,
,
Переходя к операторной форме записи, получаем:
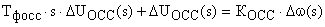 ,
,
Преобразовывая это уравнение, получаем передаточную функцию обратной связи по скорости:
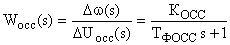 .
.
2.3. Датчики положения механизма.
В подавляющем большинстве станочного оборудования с числовым программным управлением используются измерительные преобразователи перемещения с импульсным или цифровым выходными сигналами. К ним относятся измерительные электромагнитные, электромашинные и фотоэлектрические преобразователи перемещения исполнительного механизма. В подавляющем своем большинстве точное математическое представление измерительных преобразователей перемещения требует использование дискретной математики. Однако для широкого класса систем автоматического управления возможно представление таких устройств как безинерционных элементов с передаточной функцией вида:
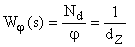 ;
;
где 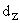 – разрешающая способность измерительного преобразователя перемещения,
– разрешающая способность измерительного преобразователя перемещения,
Дата добавления: 2015-12-29; просмотров: 1553;
