Замкнутой САУ называют систему, в которой процесс управления ОУ зависит от результата управления. 6 страница
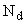 – выходной сигнал измерительного преобразователя;
– выходной сигнал измерительного преобразователя;
 — угол поворота вала измерительного преобразователя.
— угол поворота вала измерительного преобразователя.
Разрешающая способность измерительных преобразователей, связанных с валом исполнительного механизма, определяется как
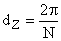 ,
,
где N – число меток измерительного преобразователя на один оборот его вала.
3. Электромеханические преобразователи
В САУ используются различные исполнительные устройства, предназначенные для выполнения необходимых технологических операций. В качестве исполнительных преобразователей могут использоваться устройства, такие как электрические машины, гидравлические и пневматические преобразователи, нагревательные и акустические приборы. В технологическом оборудовании, используемом в механообработке, наиболее часто используются электромеханические преобразователи, в качестве которых используются электрические машины. Наиболее часто применяются электродвигатели постоянного тока, асинхронные электродвигатели и синхронные электрические машины, работающие в режиме бесконтактного двигателя. Рассмотрим их основные характеристики, которые необходимы для их рассмотрения, как объектов теории автоматического управления.
3.1. Электродвигатель постоянного тока
Двигатель постоянного тока, как элемент САУ, описывается дифференциальными уравнениями якорной цепи и механической части двигателя:
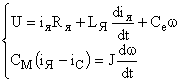 , ,
| (4) |
где 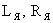 – соответственно индуктивность и активное сопротивление якорной цепи;
– соответственно индуктивность и активное сопротивление якорной цепи;
 — соответственно ток якорной цепи и ток нагрузки;
— соответственно ток якорной цепи и ток нагрузки;
 – конструктивные постоянные двигателя;
– конструктивные постоянные двигателя;
 – момент инерции двигателя.
– момент инерции двигателя.
При изменении напряжения на входе двигателя на некоторую величину  изменяются ток двигателя
изменяются ток двигателя 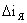 и частота вращения двигателя
и частота вращения двигателя 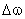 и, пренебрегая обратной связью по противоЭДС двигателя
и, пренебрегая обратной связью по противоЭДС двигателя 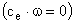 , получаем уравнения якорной цепи и механической части двигателя в приращениях:
, получаем уравнения якорной цепи и механической части двигателя в приращениях:
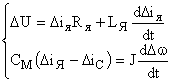
| (5) |
Преобразовывая уравнения (5) и, считая  , переходим к операторной форме записи данных уравнений:
, переходим к операторной форме записи данных уравнений:

| (6) |
Из уравнений (6) получаем выражения для передаточных функций якорной цепи и механической части двигателя:

где 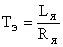 – электромагнитная постоянная двигателя,
– электромагнитная постоянная двигателя,
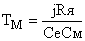 — электромеханическая постоянная двигателя.
— электромеханическая постоянная двигателя.
Согласно этой системе получаем, что развернутая структурная схема двигателя принимает вид, показанный на рис.1.

Рис. 1. Развернутая структурная схема двигателя
Свертывая развернутую схему, двигатель можно представить одним колебательным звеном (рис. 2):
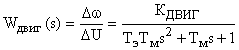 ,
,
где 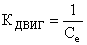 .
.

Рис. 2. Свернутая структурная схема двигателя
3.2. Асинхронный электродвигатель
Асинхронный электродвигатель является наиболее широко используемой электрической машиной. Это объясняется простотой его конструкции и достаточно жесткими механическими характеристиками. Механическая характеристика имеет вид, представленный на рис. 3.
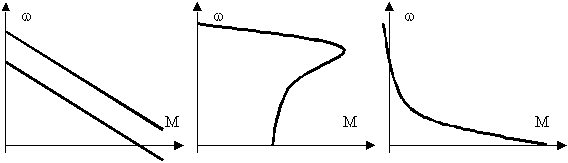
Рис. 3. Сравнительные механические характеристики электродвигателей.
Конструктивно асинхронный двигатель состоит из ротора, на котором расположена короткозамкнутая обмотка типа "беличья клетка", и статора. На статоре расположены обмотки управления, число которых определяется числом фаз питающего напряжения. Синхронная частота вращения вала двигателя определяется как
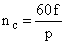 ,
,
где  – частота питающего напряжения
– частота питающего напряжения
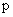 – число пар полюсов статорной обмотки.
– число пар полюсов статорной обмотки.
Для управления асинхронными двигателями используются частотные и амплитудные методы. В первом случае регулирование частоты вращения осуществляется путем изменения частоты питающего напряжения. Во втором случае для изменения частоты вращения вала асинхронного двигателя изменяется напряжение, подаваемое на статорные обмотки двигателя.
Точное математическое описание процессов, происходящих в асинхронном двигателе, представляется системой уравнений Парка-Горева. Оно используется при детальном рассмотрении систем автоматического управления с такими двигателями. Но так как, электромагнитные процессы, протекающие в асинхронных двигателях достаточно быстротечны, при их рассмотрении в большинстве приложений рассматривают только электромеханическую их составляющую. Поэтому передаточная функция асинхронного двигателя в большинстве приложений представляется как
 ,
,
где 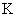 – коэффициент пропорциональности между угловой скоростью вала и управляющим сигналом,
– коэффициент пропорциональности между угловой скоростью вала и управляющим сигналом,
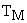 – электромеханическая постоянная времени двигателя и исполнительного механизма.
– электромеханическая постоянная времени двигателя и исполнительного механизма.
3.3. Бесконтактный электродвигатель
В приводах подачи металлообрабатывающих станков широкое применение находят бесконтактные (бесколлекторные) двигатели (БКД). Такие электромеханические преобразователи состоят из синхронного двигателя, с ротором которого связан датчик положения ротора. Этот датчик обеспечивает коммутацию обмоток управления, расположенный на статоре электрической машины. На ее роторе располагаются постоянные магниты. Функциональная схема такого электромеханического преобразователя представлена на рис. 4.
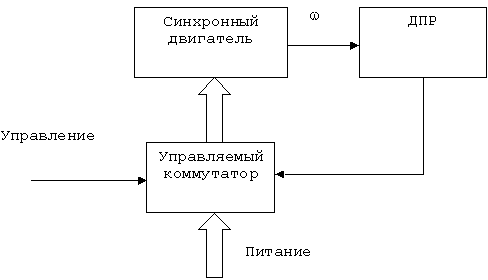
Рис. 4. Функциональная схема БКД.
Момент, развиваемый БКД определяется как:
 ,
,
где 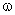 — угловая скорость вала,
— угловая скорость вала,
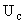 – напряжение управления двигателем,
– напряжение управления двигателем,
 – сопротивление и индуктивность фазной обмотки двигателя,
– сопротивление и индуктивность фазной обмотки двигателя,
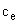 – коэффициент пропорциональности между напряжением на фазных обмотках двигателя и угловой скоростью его вала,
– коэффициент пропорциональности между напряжением на фазных обмотках двигателя и угловой скоростью его вала,
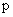 – число пар полюсов двигателя,
– число пар полюсов двигателя,
 – число фаз обмотки управления,
– число фаз обмотки управления,
 — угол сдвига между основной гармоникой ЭДС фазы и фазовым напряжением.
— угол сдвига между основной гармоникой ЭДС фазы и фазовым напряжением.
При малой индуктивности фазных обмоток двигателя и величине угла сдвига между основной гармоники ЭДС и фазовым напряжением, близким к 90 градусов, величина момента, развиваемого БКД, определяется как
 .
.
Таким образом, вид механической характеристики БКД достаточно близок к аналогичным характеристикам двигателя постоянного тока. Поэтому, для исследования САУ, содержащих бесконтактные двигатели, используются передаточные функции, полученные для двигателей постоянного тока.
4. Механические системы.
Механизмы передачи крутящих моментов широко используются для согласования скоростей рабочих машин или исполнительных механизмов и приводных двигателей. Среди них наибольшее распространение находят зубчатые передачи.

Рис. 5. Пример простейшей кинематической передачи.
Динамические процессы, происходящие в большинстве механизмов, неразрывно связаны со свойствами входящих в него механических систем. Особенности получения динамических моделей механизмов с линейными функциями положения и линейными характеристиками упругих звеньев можно рассмотреть на примере механической системы, представленной на рис. 5. Здесь ротор двигателя М и вращающееся исполнительное звено MM связаны передаточным механизмом, состоящим из зубчатых колес 1-4, образующих двухступенчатый редуктор. Пусть передаточное отношение первой пары —  , а
, а 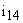 – общее передаточное число редуктора. Моменты инерции всех звеньев относительно их собственных осей –
– общее передаточное число редуктора. Моменты инерции всех звеньев относительно их собственных осей –  .
.
При составлении динамической модели механизма будем учитывать крутильные податливости соединительных валов и зубчатых передач. При этом под податливостью понимается величина, обратная жесткости вала с, которая определяется как
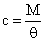 ,
,
где 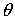 — угол закручивания элемента механизма.
— угол закручивания элемента механизма.
Вычисление податливости валов, связывающих элементы рассматриваемого механизма, подробно описано в литературе по теоретической и прикладной механике. Для вычисления жесткости зубчатой передачи со стальными зубьями можно пользоваться эмпирической зависимостью:
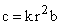 ,
,
где 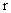 – радиус ведущего колеса, см;
– радиус ведущего колеса, см; 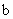 – ширина зубчатого венца, см;
– ширина зубчатого венца, см; 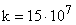 .
.
Обозначим жесткости зубчатых передач 1-2 и 3-4 как  и
и 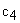 соответственно. Жесткости валов, связывающих элементы механизма, обозначим как
соответственно. Жесткости валов, связывающих элементы механизма, обозначим как 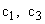 и
и 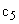 . В большинстве своем упругие элементы передаточного механизма обладают диссипативными свойствами, то есть способностью рассеивать механическую энергию. В общем случае зависимость силы сопротивления от скорости может быть достаточно сложной функцией. Коэффициент, характеризующий диссипативные свойства, может быть непостоянным, а показатель степени, в которую возводится величина скорости, отличен от единицы. Решение таких задач выходит за рамки настоящего пособия. Будем рассматривать механические системы, в которых присутствуют силы вязкого трения, пропорциональные скорости движения элементов механизма. Эти силы характеризуются коэффициентами демпфирования
. В большинстве своем упругие элементы передаточного механизма обладают диссипативными свойствами, то есть способностью рассеивать механическую энергию. В общем случае зависимость силы сопротивления от скорости может быть достаточно сложной функцией. Коэффициент, характеризующий диссипативные свойства, может быть непостоянным, а показатель степени, в которую возводится величина скорости, отличен от единицы. Решение таких задач выходит за рамки настоящего пособия. Будем рассматривать механические системы, в которых присутствуют силы вязкого трения, пропорциональные скорости движения элементов механизма. Эти силы характеризуются коэффициентами демпфирования 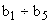 . Иными словами, полагаем, что при изменении деформации
. Иными словами, полагаем, что при изменении деформации  элемента механизма с номером r возникает момент, определяемый как
элемента механизма с номером r возникает момент, определяемый как
 .
.
Рассматриваемая система имеет шесть степеней свободы. В качестве обобщенных координат удобно принять углы поворота ротора двигателя и зубчатых колес, приведенные к ротору двигателя. То есть
 ,
, 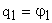 ,
, 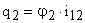 ,
,
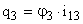 ,
, 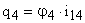 ,
, 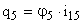 .
.
При этом деформации валов и зубчатых колес, приведенные к валу двигателя, определяются как


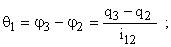
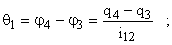

Из уравнения Лагранжа следует, что система дифференциальных уравнений, описывающая движение отдельных элементов механизма, может быть представлена в следующем виде
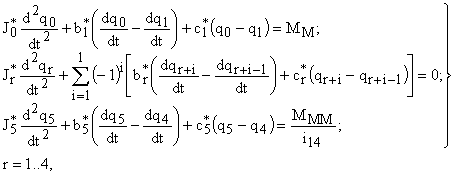
| (7) |
где 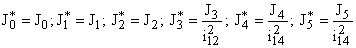 – моменты инерции звеньев, приведенные к валу двигателя,
– моменты инерции звеньев, приведенные к валу двигателя,
 — значения коэффициентов демпфирования, приведенные к валу двигателя,
— значения коэффициентов демпфирования, приведенные к валу двигателя,
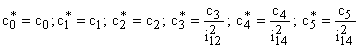 — значения жесткости элементов кинематической цепи, приведенные к валу двигателя,
— значения жесткости элементов кинематической цепи, приведенные к валу двигателя,  – момент, развиваемый приводным двигателем,
– момент, развиваемый приводным двигателем,
 – момент сопротивления рабочей машины.
– момент сопротивления рабочей машины.

Рис. 6. Цепная динамическая модель механизма.
На рис. 6 представлена цепная динамическая модель механизма, для которой уравнения вынужденных колебаний, вызываемых активными приложенными силами и моментами инерции, совпадают с движениями, возникающими в системе, представленной выражением (7).
На рисунке 6 принято, что величина динамического момента 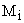 определяется как
определяется как
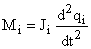 .
.
Таким образом, динамические ошибки, вызванные податливостью звеньев, могут рассматриваться как вынужденные крутильные колебания многомассовой системы вблизи траектории программного движения механизма с абсолютно жесткими звеньями.
Система уравнений (7) в операторной форме записывается как
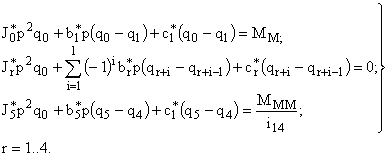
| (8) |
Из системы (8) определяются передаточные функции, связывающие законы изменения обобщенных координат с законами изменения обобщенных сил. Соответствующие им частотные характеристики имеют размерность податливости. Кроме того, возможно получение передаточных функций, связывающих величины обобщенных сил с моментами, прикладываемыми к редуктору со стороны двигателя и исполнительного механизма. Такие характеристики позволяют определить величины динамических моментов, возникающих в различных элементах механизма при разных режимах его работы.
Так как основные параметры зубчатых передач определяются исходя из требуемой нагрузочной способности, то в подавляющем большинстве случаев податливости спроектированных зубчатых колес значительно меньше податливостей элементов их соединения с рабочей машиной и приводным двигателем. Поэтому с достаточной степенью точности можно утверждать, что жесткости зубчатых колес общепромышленных механизмов бесконечно велики. Исходя из этого эвристического положения, двухступенчатый редуктор можно рассматривать как трехмассовую систему, параметры которой определяются следующим образом:
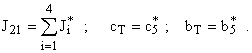
Структурная схема такого представления двухступенчатого редуктора показана на рис. 7.

Рис. 7. Структурная схема механизма с двухступенчатым редуктором
На рис.8 изображены логарифмическая (а) и амплитудно-фазовая (б) частотные характеристики такого механизма.

Рис. 8. Частотные характеристики двухступенчатого редуктора (а – логарифмическая, б — амплитудно-фазовая)
5. Процесс механообработки
При рассмотрении процесса обработки заготовки на токарном станке следует отметить, что при движении резца под действие сил. Возникающие в процессе резания силы, действующие в осевом направлении, вызывают деформацию резца. Величина этой силы может быть определена как
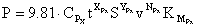 ,
,
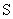 – продольная подача на оборот;
– продольная подача на оборот;
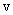 – скорость резания в мм/мин;
– скорость резания в мм/мин;
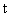 – глубина резания в мм;
– глубина резания в мм;
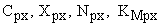 – коэффициенты, постоянные для выбранного режима обработки. Их значение можно принять постоянным и равным К. При
– коэффициенты, постоянные для выбранного режима обработки. Их значение можно принять постоянным и равным К. При 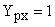 можно считать, что
можно считать, что
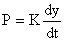 ,
,
где y – действительное перемещение режущей кромки резца.
При перемещении резцедержателя на некоторую величину xвеличина перемещения его режущей кромки y будет отличаться от этого значения на величину стрелы прогиба резца. Наличие этой деформации 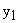 определяется жесткостью резца. Хотя конечной величиной жесткости характеризуются все элементы станка, для большинства расчетов их податливостью пренебрегают. Сила, вызванная упругой деформацией резца
определяется жесткостью резца. Хотя конечной величиной жесткости характеризуются все элементы станка, для большинства расчетов их податливостью пренебрегают. Сила, вызванная упругой деформацией резца 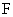 , определяется как:
, определяется как:
 ,
,
где 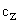 – приведенная жесткость режущего инструмента.
– приведенная жесткость режущего инструмента.
Условием равновесия точки резания является уравнение вида:
 ,
,
где  – приведенная масса системы "резец – резцедержатель".
– приведенная масса системы "резец – резцедержатель".
С учетом уравнения определения силы упругой деформации резца получаем, что
 .
.
Тогда уравнение движения режущей кромки инструмента определяется как
 ,
,
где  ,
,  .
.
Полученное дифференциальное уравнение указывает на то, что рассматривая часть технологического процесса представляет звено второго порядка. Это указывает на теоретическую возможность появления затухающего колебательного процесса. На практике вследствие малости приведенной массы  величиной компоненты, обусловленной ускорением режущей кромки можно пренебречь. Поэтому уравнение движения можно представить как:
величиной компоненты, обусловленной ускорением режущей кромки можно пренебречь. Поэтому уравнение движения можно представить как:
 .
.
Передаточная функция процесса резания определяется как
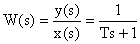 .
.
Вопросы.
1. Какие основные элементы используются в системах автоматического управления?
2. Для чего используются исполнительные двигатели?
3. Какая передаточная функция характеризует двигатель постоянного тока?
4. Что называется бесколлекторным двигателем? Какая передаточная функция используется для его представления?
5. Какая передаточная функция характеризует асинхронный двигатель?
6. Какая математическая модель используется при представлении динамических свойств силовых преобразователей?
7. Какая математическая модель используется при представлении динамических свойств исполнительных механизмов?
8. Что называется упругостью механизма? Какие его свойства характеризует упругость механизма?
9. Какие математические модели используются при представлении измерительных преобразователей?
10. Как получить математическое описание регулятора, построенного на базе операционного усилителя?
11. Как определить передаточную функцию многомассовой системы?
12. Как динамически представляется процесс резания.
13. Какой вид имеет структурная схема многомассовой системы?
14. Какой вид имеет структурная схема двигателя постоянного тока?
Тема 7. Устойчивость и наблюдаемость систем автоматического управления.
В статическом режиме работы все составляющие вектора состояния САУ не зависят от момента времени их рассмотрения и остаются постоянными, соответствующими условию равновесия системы. Это состояние в зависимости от структуры и параметров САУ может быть устойчивым или неустойчивым. Если после изменения вектора внешних воздействий система приходит в состояние, при котором все составляющие вектора ее состояния становятся постоянными, то есть система возвращается в положение равновесия, то это состояние равновесия является устойчивым. В случае, когда после изменение входного сигнала или возмущения, система не стремится в первоначальное состояние, а вектор выходных сигналов изменяется независимо от внешнего воздействия, то такое состояние является неустойчивым. В этом случае система автоматического управления является неустойчивой. Графическая интерпретация таких режимов работы САУ представлена на рис. 1.
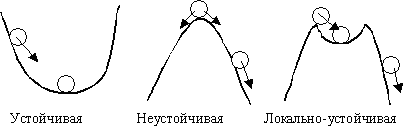
Рис. 1. Графическая интерпретация устойчивости.
Под устойчивостью понимается свойство САУ возвращаться в исходное состояние после вывода ее из этого состояния и прекращения влияния задающего или возмущающего воздействия.
Только устойчивая система автоматического управления может выполнять возложенные на нее функции. Поэтому одной из основных задач САУ является обеспечение ее устойчивости.
Основы теории устойчивости САУ были заложены А.М. Ляпуновым в его работе "Общая задача устойчивости движений", опубликованной в 1882 г.
Если САУ представляется системой линейных дифференциальных уравнений, то ее устойчивость не зависит от величины и точки приложения внешних возмущений.
Нелинейные системы могут быть устойчивы при малых возмущениях и неустойчивы при больших возмущениях. Теорема Ляпунова устанавливает, что об устойчивости нелинейных систем при малых возмущениях можно судить по их линеаризованным уравнениям, достаточно адекватно описывающих поведение САУ при малых отклонениях от положения равновесия. Поэтому будем рассматривать только вопросы устойчивости САУ, представляемых линейными или линеаризованными дифференциальными уравнениями.
7.1. Математический признак устойчивости.
При нарушении равновесия САУ, вызванного внешним воздействие, возникают переходные процессы. Вид переходного процесса зависит как от свойств системы, так и от вида возмущения. В переходном процессе присутствуют 2 составляющие: 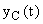 — свободные движения системы, определяемые начальными условиями и свойствами САУ;
— свободные движения системы, определяемые начальными условиями и свойствами САУ; 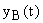 вынужденные движения, определяемые возмущением и свойствами системы. Вид переходного процесса определяется как
вынужденные движения, определяемые возмущением и свойствами системы. Вид переходного процесса определяется как
 .
.
Чтобы САУ могла достоверно отображать задаваемую информацию необходимо, чтобы в переходном процессе свободная составляющая с течением времени должна стремиться к нулю, то есть должно выполняться условие вида:
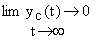 .
.
Характер свободного движения системы определяет ее устойчивость или неустойчивость. Возможные виды переходных процессов в САУ представлены на рис. 1.
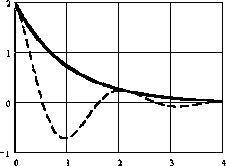

Рис. 2. Виды кривых переходных процессов.
Рассмотрим дифференциальное уравнение линейной САУ.
7.2. Критерии устойчивости линейных САУ.
Прямой анализ устойчивости САУ, основанный на вычислении корней характеристического уравнения, связан с необходимостью вычисления корней, что является непростой задачей. Поэтому в инженерной практике важное значение приобретают правила, позволяющие определять устойчивость системы без вычисления корней характеристического уравнения.
Способы определения устойчивости САУ без вычисления корней характеристического уравнения называются критериями устойчивости САУ. Различают две группы критериев устойчивости: алгебраические – основанные на анализе коэффициентов характеристического уравнения, и частотные – основанные на анализе частотных характеристик САУ.
7.2.1. Алгебраический критерий Гурвица
Этот критерий позволяет определить устойчивость САУ, если характеристическое уравнение замкнутой системы представлено в виде:

Для этого строится главный определитель Гурвица по следующему правилу: по главной диагонали выписываются все коэффициенты от  до
до 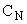 в порядке возрастания коэффициентов. Столбцы вверх от главной диагонали заполняются коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз – коэффициентами с последовательно убывающими индексами. На месте коэффициентов с индексами, большими порядка характеристического уравнения и меньшими нуля, проставляют нули.
в порядке возрастания коэффициентов. Столбцы вверх от главной диагонали заполняются коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз – коэффициентами с последовательно убывающими индексами. На месте коэффициентов с индексами, большими порядка характеристического уравнения и меньшими нуля, проставляют нули.

Выделяя в главном определителе Гурвица диагональные миноры, получаем определитель Гурвица низшего порядка. Номер определителя Гурвица определяется номером коэффициента по диагонали, до которого составляют данный определитель.
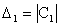 ,
, 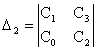 ,
,  .
.
Дата добавления: 2015-12-29; просмотров: 1719;
