Замкнутой САУ называют систему, в которой процесс управления ОУ зависит от результата управления. 3 страница

Если число последовательно соединенных элементов больше трех, то предварительно строится характеристики групп из трех элементов, а затем к полученным статическим характеристикам применяется описанная методика.

Рассмотрим методику определения статической характеристики САУ, охваченной обратной связью.

Пусть статические характеристики элементов определяются функциями вида:

, .

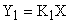Результирующая характеристика определяется функцией вида:

.

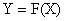Графическое представление этих характеристик представлено на рис. 6, где по оси абсцисс откладывается значение входного сигнала Х сигнала ошибки управления ( 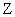) и выходного сигнала канала обратной связи , а по оси ординат – выходной сигнал САУ.

Рис. 5. Построение статической характеристики элемента, охваченного обратной связью.

Для построения результирующей характеристики выбираются значения выходного сигнала . абсциссы точек пересечения этой прямой с рассматриваемыми частотными характеристиками дают значения сигнала ошибки – 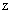и сигнала на выходе элемента, расположенного в цепи обратной связи- .

.

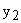Соединяя плавной линией множество полученных точек получаем результирующую характеристику САУ, включающую замкнутый контур управления. Если необходимо получить статическую характеристику САУ, содержащую в прямом и обратном канале комбинацию элементов с нелинейными характеристиками, то первоначально определяют статические характеристики прямого канала и обратной связи. Затем, по изложенной выше методике, строят характеристику САУ с обратной связью.

Хорошие результаты при определении результирующих статических характеристик САУ дает использование программных комплексов MathCAD и MathLAB.

3.3. Линеаризация статических характеристик САУ

Обычно статические характеристики элементов САУ существенно нелинейных, что затрудняет, а иногда делает невозможным, процесс их исследования и проектирования. Для упрощения решения этой задачи производят реализацию статических характеристик.

Линеаризацией называется замена реальных нелинейных уравнений статических характеристик САУ близкими к ним линейными уравнениями. Для линеаризации характеристик САУ используется метод малых отклонений.

Рассмотрим систему, статическая характеристика которой представляется нелинейным уравнением вида:

.

Графическое представление этой характеристики показано на рис. 7. В установившемся режиме работы САУ на входе и выходе рассматриваемого элемента устанавливаются определенные значения соответствующих сигналов, определяемые режимом работы системы. То есть для любого режима работы с САУ справедливо следующее равенство:

.

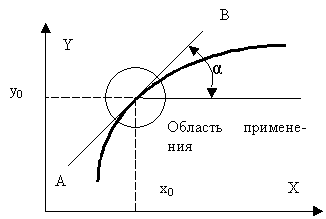
Рис. 6. Графическая интерпретация линеаризации статических характеристик.

Функцию, имеющую n непрерывных производных, можно разложить в ряд Тейлора. Эта операция дает следующий результат:

,

где 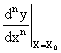— n-ая производная искомой функции в точке установившегося режима работы.

При малых отклонениях от положения равновесия величина . Поэтому все слагаемые разложения в ряд Тейлора будут много меньше, чем два первых. То есть можно считать, что

.

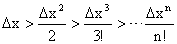Исходя из этого можно считать, что

.

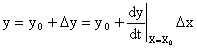Из этого выражения следует, что

.

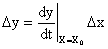Величина 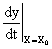равна тангенсу угла наклона касательной, проведенной к кривой статической характеристики 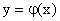в точке 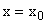. Это показано на рис. 7. То есть

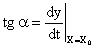
Следовательно, уравнение линеаризованной характеристики можно представить как:

,

где 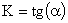— коэффициент передачи линеаризованного элемента или системы.

Отсюда следует, что при линеаризации нелинейное уравнение заменяется линейным уравнением в приращениях рассматриваемых переменных.

Аналогичный подход используется, если выходной сигнал устройства является функцией нескольких входных переменных. То есть

.

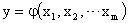Для линеаризации статических характеристик такого вида определяют частные производные по каждому входному воздействию.

После разложения в ряд Тейлора получаем, что

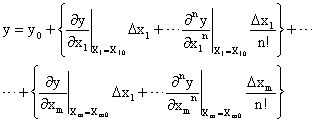
Пренебрегая всеми производными, кроме первых для каждой входной переменной, получаем, что с достаточной степенью точности выходной сигнал элемента определяется как:

Из этого уравнения следует, что приращение выходного сигнала определяется как

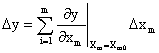
Следовательно, элемент САУ с несколькими входными сигналами может быть представлен как совокупность нескольких линейных элементов и сумматора, объединяющего выходные сигналы этих элементов.

Область применения такого подхода к линеаризации статических характеристик САУ ограничивается наличием непрерывных производных у исходной функции. При наличии разрывов в производных исходной функции, что характерно для элементов с существенно нелинейными характеристиками, такой способ, строго говоря, не применим к точкам, в которых непрерывность производных не обеспечивается.

Для примера рассмотрим линеаризацию статической характеристики вида:

.

Производная этой функции определяется как

.

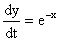Следовательно, линеаризованная характеристика рассматриваемого элемента определяется как:

.

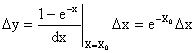Коэффициент передачи линеаризованного элемента 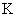определяется как

.

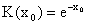Вопросы.

1. Что называется статической характеристикой САУ и ее элементов?

2. Какие виды статических характеристик САУ вам известны?

3. Что называется статическим линейным элементов?

4. Какие особенности присущи астатическим элементам?

5. Дайте определение статической САУ?

6. Дайте определение астатической САУ?

7. Чем отличаются статические и астатические системы автоматического управления?

8. Что называется добротностью элемента или системы?

9. Какие способы соединения элементов САУ вам известны?

10. Как определить статическую характеристику САУ, состоящей из последовательно соединенных элементов?

11. Как определить статическую характеристику САУ, состоящей из параллельно соединенных элементов?

12. Какие способы используются для построения статических характеристик САУ?

13. Как графически определяется статическая характеристика замкнутой САУ?

14. Для каких целей используется линеаризация статических характеристик САУ?

15. Опишите основные принципы линеаризации статических характеристик САУ?

16. Как проводится линеаризация многомерных САУ

Тема 4. Динамика линейных систем автоматического управления.

Свойства любой системы проявляются в процессе ее функционирования. Для определения этих свойств следует подавать на входы некоторые возмущающие воздействия и анализировать вектор выходного состояния САУ. При отработке различных внешних воздействий реакция системы автоматического управления зависит от ее структуры и параметров.

Рассмотрим возможную реакцию САУ на ступенчатое воздействие, подаваемое на один из ее входов. При этом выходной сигнал может меняться апериодически (рис 1а) или при наличии нескольких затухающих колебаний (рис. 1б). Такой характер изменения выходной координаты системы характерен для устойчивых САУ.

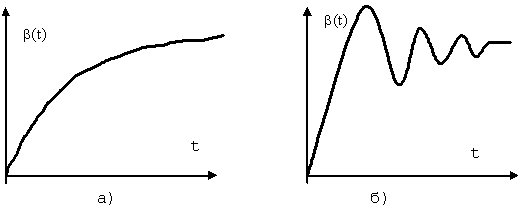
Рис. 1. Возможные переходные процессы для устойчивых САУ.

Возможен случай, когда в системе возникают незатухающие колебания. САУ, обладающие таким свойством, называются консервативными. Характер изменения выходной координаты в консервативной САУ представлен на рис. 2.

Рис. 2. Переходной процесс в консервативной САУ

Для ряда систем характерно отсутствие постоянного или периодического сигнала на выходе САУ в течение всего периода ее работы. Такие системы называются неустойчивыми. Характер изменения выходного сигнала САУ при выводе ее из положения равновесия показан на рис. 3.

Как рассматриваемая система автоматического управления будет отрабатывать внешние воздействия, каков характер переходного процесса и обеспечивается ли его устойчивость – вот основные вопросы, которые рассматриваются при исследовании динамики систем автоматического управления. Прямой путь решения этой задачи – это проведение натурных экспериментов с реальными системами автоматического управления. Однако проведение таких экспериментов с реальной системой экономически невыгодно, а с проектируемой – невозможно. Поэтому эксперименты для изучения свойств САУ проводят не с реальными системам, а их моделями.

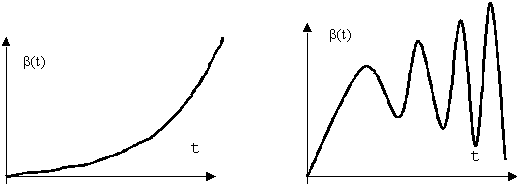
Рис. 3. Характер изменения выходной координаты неустойчивой САУ.

Модель – некоторая система, сохраняющая существенные черты оригинала и допускающая ее исследование физическими или математическими методами. Моделирование — это процесс проведения экспериментов на модели вместо прямых экспериментов на самой системе. В настоящее время моделирование наиболее широко применяемый способ научного познания реальной действительности. Очень часто моделирование – это единственное средство познания сложных систем.

Если поставлена задача составления исходных дифференциальных уравнений САУ, то возможны две ситуации. Либо детальная декомпозиция системы на модули и отдельные звенья возможна, либо нет.

Если декомпозиция возможна, то, опираясь на постулаты о сохранении материи и энергии (для соответствующего энергетического домена) и на закон Ома (в соответствующей формулировке), приступают к составлению исходных дифференциальных уравнений САУ, т.е. к созданию истинной модели системы. Истинной будем называть такую модель или такое математическое описание, о которых известно, что они детально соответствуют физической природе системы.

Если декомпозиция на модули и звенья для системы невозможна, то, не имея детальной информации о ее физической природе, можно получить лишь упрощенную модель или упрощенное математическое описание, которые, однако, позволят исследовать систему и получить адекватные результаты. В этом случае совокупность исходных дифференциальных уравнений САУ получают через частотный домен, путем экспериментального снятия частотных характеристик.

Для физической системы порядок системы дифференциальных уравнений ее истинной модели обычно в десять и более раз выше порядка системы дифференциальных уравнений ее ложной модели (например, для моделей операционных усилителей). Тем обусловлена широкая популярность ложных моделей, и типовых звеньев, как структурных элементов для их создания.

Дифференциальное уравнение САУ или уравнение динамики ее движения – это уравнение, определяющее зависимость выходного сигнала от входной переменной 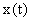. В общем виде оно может быть представлено как:

(1)

где 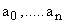и 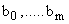– некоторые коэффициенты, значения которых в общем случае не являются постоянными.

Решение (1) определяет поведение системы автоматического управления в динамических режимах работы.

Вводя в рассмотрение алгебраический оператор дифференцирования вида

,

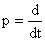получаем запись дифференциального уравнения (1) в операторной форме записи.

.

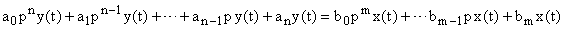Полученное алгебраическое уравнение позволяет определить связь между входной и выходной переменной САУ как

.

Связь между выходной и входной переменными можно определить как

.

(2)

Это выражение не является абсолютно строгим, так как используется оператор p, выполняющий операцию дифференцирования.

Составление основных уравнений систем автоматического управления (САУ) может быть облегчено, если рассматривать ее как комбинацию динамических звеньев с определенными передаточными функциями. Изображение САУ в виде совокупности динамических звеньев с указанием взаимосвязи между ними называется структурной схемой системы. Структурная схема может быть составлена на основе известных уравнений системы и, наоборот, дифференциальные уравнения могут быть получены из структурной схемы. При этом первая задача может иметь различные варианты решения, тогда как вторая всегда имеет единственное решение.

В целях формализации процесса составления исходных дифференциальных систем используют такие методы, как "Метод контурных токов", "Метод узловых потенциалов" и их аналоги, имеющиеся во всех энергетических доменах. В результате их применения получается единая система:

(3)

где:

— обобщенные координаты системы, в том числе (для САУ) ошибка — 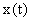и регулируемая величина — ;

– полиномы от оператора 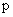, определяемые свойствами САУ. Они могут быть постоянными или зависящими от условий работы системы;

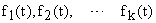— внешние координаты — задающие и возмущающие 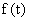воздействия;

— алгебраизированный оператор дифференцирования.

Совокупность уравнений (1) может быть решена относительно любой обобщенной координаты.

Для удобства и формализации решений систему уравнений (3) могут представить в одной из пяти стандартных форм:

· в форме Коши;

· в пространстве состояний;

· в виде передаточных функций — .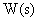

Рассмотрим форму Коши, как способ представления уравнение динамики движения системы. При этом используется матричная форма записи системы дифференциальных уравнений решенных исключительно относительно первой производной координат САУ.

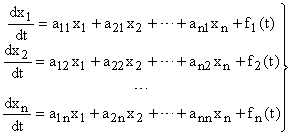
(4)

где:

— собственные координаты системы, в которые входят ошибка системы 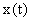, воздействие на объект 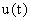, выходная координата — ,...;

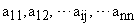_n — постоянные или переменные коэффициенты, определяемые структурой и параметрами системы автоматического управления;

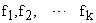— воздействия на систему — сигнал задания или помехи .

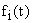Уравнения могут быть решены относительно любой из фазовых координат .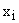

В виде (4) форма Коши применяется в теории управления не часто. Она удобна, если для расчетов использовать классические математические пакеты: MathCAD, MATLAB, Mathematica, Maple. Форма Коши используется при построении аналоговых вычислительных моделей матричного типа (например, моделей на операционных усилителях).

В общем случае система дифференциальных уравнений (4) является нелинейной. Поэтому ее использование для решения задач анализа и синтеза САУ в аналитической форме затруднено. Поэтому в теории автоматического управления широко используется методы линеаризации систем дифференциальных уравнений. Наиболее часто применяемым является метод малых отклонений, основанный на представлении нелинейных характеристик отрезками прямых и замене действительных значений переменных отклонениями от выбранного положения равновесия. Применение этого метода к дифференциальным уравнениям базируется на способах, используемых при линеаризации статических характеристик САУ, как это было показано ранее.

В последнее время для представления уравнения движения САУ широко используется метод пространства состояний, который представляет собой ничто иное, как представления системы (4) в матричной форме записи.

Уравнения движения произвольной системы автоматического управления можно записать в виде:

для I=1,..N

(5)

где – Х- координаты системы. Частью из них можно управлять с помощью M уравнений 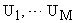-, характеризующих влияние функций управления, внешних возмущений или изменений параметров. 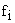— некоторая функция всех перечисленных аргументов. Эти уравнения записываются на основе физических законов Ньютона, Кирхгофа, математического или энергетического баланса и т.п. При этом выходные сигналы САУ Y определяется векторным уравнением вида:

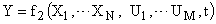
(6)

где 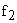– некоторая функция координат системы, а также внешних возмущений и управляющих воздействий.

Далее мы будем иметь дело с векторной формой записи уравнений (5) и (6) в виде:

,

.

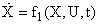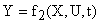где

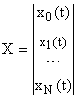— вектор состояния системы;

— вектор внешних воздействий на САУ, включающий в себя управляющие и возмущающие воздействия на САУ;

— вектор выходных сигналов САУ.

Из всего множества таких систем будем рассматривать только те разделы, которые представляют фундамент теории линейных систем автоматического управления, описываемых уравнениями:

(7)

где 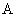— матрица размерности 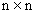с элементами ;

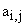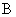— матрица размерности 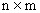с элементами ,

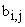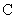— матрица размерности 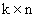с элементами ,

— матрица размерности 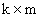с элементами ,

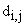Основное внимание будем уделять стационарным системам, в которых элементы матриц А, В, C и D являются постоянными. Если использовать символьную форму записи дифференциальных уравнений, которой применяется алгебраизированный оператор дифференцирования, то вышеприведенная система уравнений принимает вид:

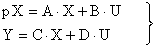
Вышеприведенная система уравнений может быть представлена в виде структурной схемы САУ, показанной на рис. 4

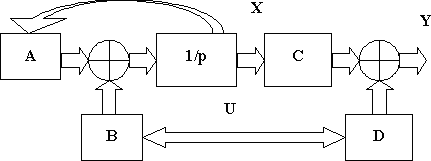
Рис. 4. Структурная схема САУ в пространстве состояний.

Прежде чем рассмотреть управленческие аспекты задачи управления, исследуем свободное и вынужденное движение системы управления. Для этого полагаем, что уравнение системы описывается системой линейных дифференциальных уравнений вида:

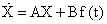
с начальными условиями ,

где

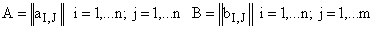
Напомним, что в случае уравнение (1) называется неоднородным дифференциальным уравнением. Его решение содержит, как известно, свободную и вынужденные составляющие.

Начнем исследования с изучения переходных процессов в системе (3) для случая, когда ее движение обусловлено лишь ненулевыми начальными условиями, то есть .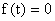

В этом случае поведение системы описывается однородным дифференциальным уравнением вида:

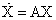
(8)

Найдем решения этого уравнения в виде:

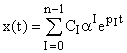
Дадим геометрическую интерпретацию решения линейного однородного уравнения (8) и определим особенности движения такой динамической системы.

Рис. 5. Геометрическая интерпретация понятия состояния САУ

Рассмотрим n-мерное пространство, по осям которой отложим координаты системы 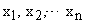. Такое пространство называется пространством состояний. Начальные условия задаются в этом пространстве (рис. 5). Так как все координаты — это функции времени, то точка будет описывать некоторую траекторию. В любой момент времени вектор можно по системе собственных векторов матрицы А с коэффициентами разложения, равными 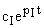. При таком разложении каждая из проекций определяется лишь одной экспонентой с показателем, равным соответствующему собственному числу 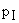. Величина определяется начальными условиями. Выберем начальные условия таким образом, чтобы . Тогда решение принимает вид:

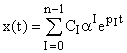
Разложим в любой момент времени вектор 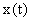по системе собственных векторов . Для n=3 и 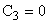это движение будет происходить в некоторой плоскости, образованной двумя собственными векторами и .

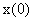Если при вектор лежит в этой плоскости, то и вектор 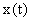лежит в этой плоскости при любом 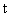. Таких плоскостей 3 в рассмотренном примере или n — в системе произвольного порядка.

Таким образом, произвольная траектория в пространстве состояний является пространственной кривой, если все . Но в тоже время в пространстве состояний существует n особых плоскостей, обладающих следующей особенностью: если в начальный момент вектор состояния находится в этой плоскости, то при дальнейшем движении вектор состояния из этой плоскости не выходит, или траектория движения целиком принадлежит этой плоскости. Такая плоскость называется инвариантным подпространством матрицы А.

Метод пространства состояний позволяет исследовать точность, устойчивость и качество процессов управления. Задача о качестве управления рассматривается в следующем смысле — необходимо выбрать такое корректирующее устройство или совокупность корректирующих устройств, чтобы система с обратной связью имела желаемое распределение корней, что практически однозначно определяет поведение системы в динамических режимах: время регулирования, колебательность, перерегулирование и т.д.