Приемы анализа вариационных рядов.

Закономерные изменения частот за счет изменения варьирующего признака в вариационных рядах называется закономерностями распределения.

Главной задачей анализа вариационных рядов является выявление закономерностей распределения и характера распределения.

Например, распределение рабочих по уровню заработной платы зависит от условий:

- квалификации;

- нормы выработки;

- расценок;

- условий труда – это общее условие.

Тип закономерности распределения – это отражение в вариационных рядах общих условий, определяющих распределение в однородной совокупности. Общие условия, определяющие тип закономерностей, познаются анализом сущности явления тех его свойств и условий, которые определяют изменчивость вариационного признака. Следовательно, должна быть построена кривая распределения. Кривая распределения – это графическое изображение частот варьирующего ряда в виде непрерывной линии, где частоты связаны с вариантами функционально. Существует теоретическая кривая распределения и фактическая.

Теоретическая кривая выражает общую закономерность данного распределения в чистом виде исключающую влияния случайных условий.

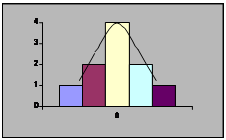Рис. 4. Полигон распределения

Полигон распределения – непрерывная линия, характеризующая фактическую кривую распределения, поскольку в нем отражаются как общие, так и случайные условия, определяющие распределение.

В статистике наиболее часто для сопоставления фактических и теоретических кривых используют нормальный тип распределения, который имеет следующее уравнение:

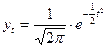
где 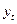- ордината кривой нормального распределения /частость/, 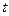- это нормированное распределение .

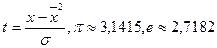В экономической статистике кривая нормального распределения (рис. 5) встречается достаточно редко, но нормальное распределение может служить моделью для выяснения степени и характера отклонения от нее фактического распределения.

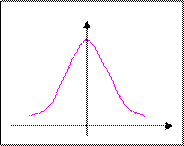Рис. 5. Кривая нормального распределения

Выравнивание фактического распределения по кривой нормального распределения.

Cостоит из нескольких этапов:

- сравнивают фактические и теоретические частоты. По фактическим данным определяют теоретические частоты кривой нормального распределения, которая является функцией нормированного отклонения;

- проверяют на сколько распределение признака соответствует нормальному.

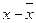
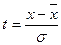
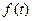
					Теоретическая частота	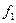Комулятивная частота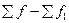
фактич.	теоретич.
		45,2	2,469	0,01888	1,2895		1,3	0,7
		35,2	1,240	0,06316	4,3138		5,6	1,4
		25,2	1,377	0,15395	10,5247		16,1	3,6
		15,2	0,830	0,28269	19,3077		35,4	1,6
		5,2	0,284	0,38361	26,2005		61,6	-6,6
		4,8	0,262	0,38568	26,3419		87,9	-1,9
		14,8	0,808	0,28737	19,627		107,5	0,5
		24,8	1,355	0,15822	10,806		118,3	1,7
		34,8	1,901	0,06562	4,4818		122,8	2,2

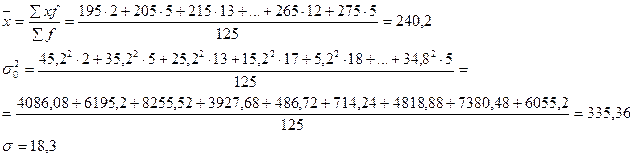
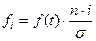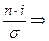; постоянное число 68,30

Рис. 6. Кривые фактического и нормального распределения

Критерии согласия.

Математическая статистика дает несколько показателей, по которым можно судить, на сколько фактическое распределение согласуется с нормальным. Эти показатели называются критериисогласия.

Критерий согласия Колмагорова (критерий 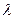) определяется путем деления max разности коммулятивных частот на корень квадратный из числа наблюдений:

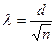, где d – максимальное отклонение фактической частоты от фактической частоты;

n – число наблюдений.

По приведенному примеру критерий =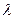

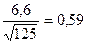
По специальной таблице вероятности для критерия согласия 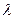определяют, что значение 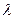=0,59 соответствует вероятности 0,88. Это значит, что с вероятностью 0,88 можно судить об отклонении фактических частот от теоретических, которые являются случайными.