ФІЗИЧНИЙ ЗМІСТ РІВНОСТІ ПАРСЕВАЛЯ

Рисунок 2.1

яке називається періодом цієї функції *, тобто

.

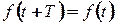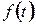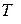Якщо періодична функція неперервна на деякому інтервалі і сonst на цьому інтервалі, то для неї існує найменший додатний період > 0. Тоді будь-який період цієї функції має вигляд .

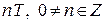Властивості періодичних функцій

1 Алгебраїчна сума, добуток і частка періодичних функцій зі спільним періодом є періодичними функціями з тим же (або меншим) періодом**.

2 Похідна періодичної функції періоду 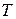є періодичною функцією з тим же періодом .

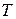3 Інтеграл від періодичної функції по періоду не залежить від місцезнаходження інтервалу інтегрування. Тобто, якщо 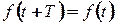, то (див. рисунок 2.2)

.

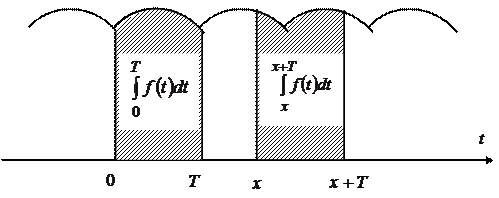
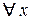
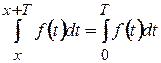Рисунок 2.2

Наслідок. Первісна періодичної функції періодична, коли середнє по періоду цієї функції дорівнює 0.

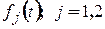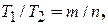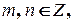4 Нехай функції є періодичними з періодами Тоді, якщо періоди спільномірні, тобто де то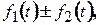

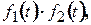
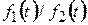є періодичними функціями^** з періодом 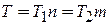(або меншим).

Зауваження. Якщо 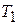і 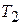неспільномірні, то 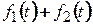вже не буде періодичною. Наприклад, функція 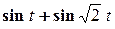неперіодична. Суми періодичних функцій з неспільномірними періодами належать більш широкому класу майже періодичних функцій.

ПРОСТА ГАРМОНІКА

Так називається дійсна періодична функція виду

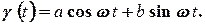(2.1)

Число 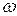називається її частотою; її період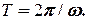

Перетворимо праву частину (2.1):

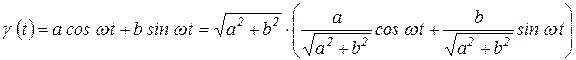. (2.2)

Позначаючи

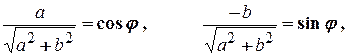(2.3)

одержуємо іншу форму запису простої гармоніки:

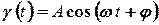, (2.4)

де число 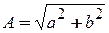> 0 називається амплітудою, а число 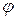- початковою фазою (при цьому *).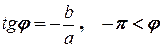

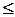
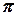Очевидно гармоніку виду (2.4) можна записати у формі (2.1). Наприклад,

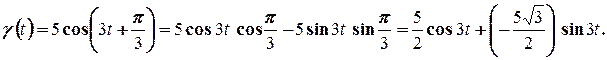
2.3 РОЗКЛАДАННЯ ПЕРІОДИЧНИХ ФУНКЦІЙ (СИГНАЛІВ) В СУМУ ПРОСТИХ ГАРМОНІК (ГАРМОНІЧНИЙ АНАЛІЗ ПЕРІОДИЧНИХ ФУНКЦІЙ (СИГНАЛІВ))

Скінченна сума простих гармонік із частотами, які кратні одній частоті, є періодичною функцією. Виникає питання: чи можна довільну періодичну функцію записати у вигляді суми гармонік?

Якщо обмежитись скінченними сумами, не можна, як показує

Приклад. Періодична функція 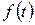на рисунку 2.3

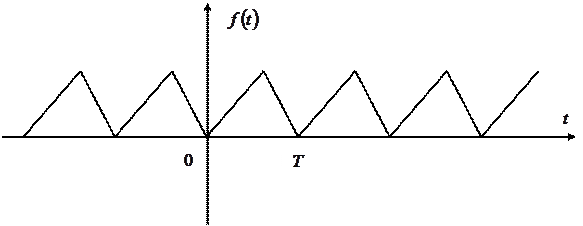Рисунок 2.3

недиференційована в точках і тому вона не дорівнює скінченній сумі гармонік, яка диференційована всюди.

Однак, якщо скінченну суму замінити нескінченною сумою (рядом), то позитивну відповідь на питання дає

Теорема 1. Нехай періодична функція 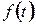періоду 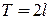є кусково гладкою на відрізку *.

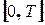Тоді 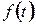в точках неперервності розкладається в ряд:

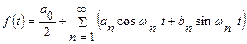, (2.5)

де 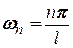, який називається її рядом Фур’є.

В точці розриву функції її ряд Фур’є збігається до 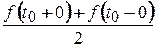(див. рисунок 2.4).

Рисунок 2.4

Числа 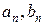називаються коефіцієнтами Фур’є функції 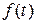і знаходяться за формулами:

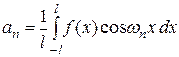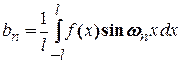
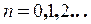, (2.6)

Зокрема 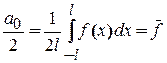– середнє значення сигналу по періоду.

Має місце рівність Парсеваля (Релея) :

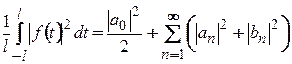. (2.7)

У випадку, коли функція 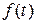дійсна, перетворимо кожний доданок в сумі (2.5) аналогічно (2.2) - (2.4) і перепишемо формулу (2.5) у вигляді

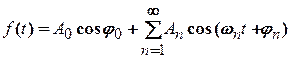, (2.8)

де

. (2.9)

Кожний доданок в сумі (2.8) описує гармонічне коливання з амплітудою 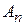, частотою 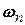, початковою фазою 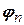. Сталий доданок 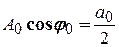називається сталою складовою сигналу , перший гармонічний доданок 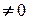- основною гармонікою або основним тоном, а наступні ненульові гармонічні доданки – верхніми гармоніками або обертонами.

Тому розкладання періодичного сигналу в ряд Фур’є , тобто в суму гармонік, називається його гармонічним аналізом.

ФІЗИЧНИЙ ЗМІСТ РІВНОСТІ ПАРСЕВАЛЯ

Враховуючи (2.9) і властивість 3 періодичних функцій, перепишемо рівність Парсеваля (2.7) у формі

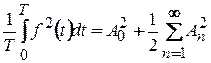. (2.10)

Нехай по провіднику з опором R тече періодичний струм i(t) з періодом Т. Розкладемо i(t) на гармоніки

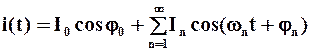. (2.11)

Рівність Парсеваля (2.10) для цього випадку після множення на R має вигляд

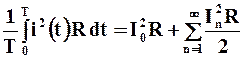. (2.12)

Ліва частина (2.12) дорівнює середній потужності струму i(t) на періоді. Перший доданок 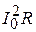в лівій частині дорівнює потужності сталої складової в розкладанні (2.11). Легко перевірити, що наступні доданки 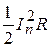дорівнюють 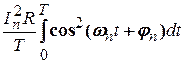- середній потужності гармонічних складових 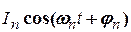на періоді.

Висновок. Формула (2.12) означає, що середня за період потужність періодичного електричного струму дорівнює сумі середніх за період потужностей його гармонічних складових плюс потужність його сталої складової.

СПЕКТРАЛЬНИЙ АНАЛІЗ ПЕРІОДИЧНОГО СИГНАЛУ

Сукупність величин 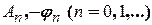з формул (2.8), (2.9) називають відповідно амплітудним та фазовим спектрами дійсного сигналу , а його частотним спектром – сукупність тих , для яких .

Графічно амплітудний та фазовий спектри зображуються стовпчиками відповідної довжини, як на рисунку 2.5.

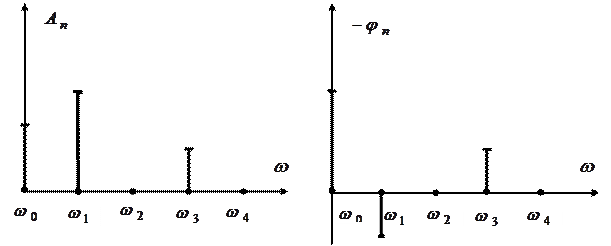Рисунок 2.5

Приклад. Який сигнал має амплітудний та фазовий спектри, що зображені на рисунку 2.6?

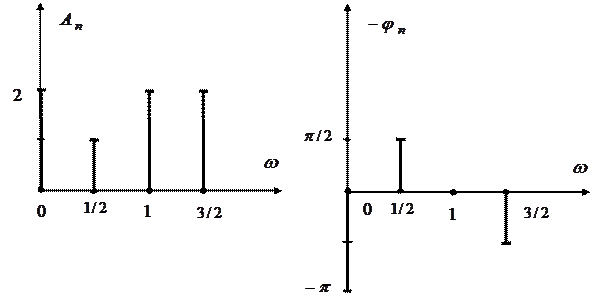
Рисунок 2.6

Розв’язок.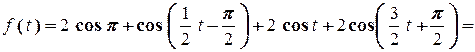

.

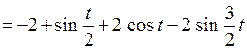РЯДИ ФУР’Є парних і непарних функцій

Коли періодична функція парна, то її коефіцієнти Фур’є 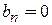і вона в точках неперервності розкладається в ряд Фур’є по косинусах

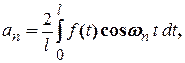
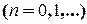, . (2.13)

Аналогічна непарна періодична функція 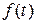розкладається в ряд Фур’є по синусах:

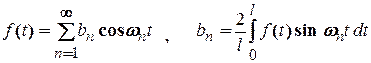. (2.14)