Статические и динамические модели

Классификация математических моделей систем

Этап построения математической модели (ММ) системы разбивается на две части: выбор структуры и выбор параметров. Структура сложной системы определяется типами моделей каждой ее подсистемы и характером связей (отношений) между ними. Все многообразие имеющихся типов ММ можно классифицировать по нескольким основным признакам (см. табл. 1): статические - динамические; дискретные - непрерывные; детерминированные - стохастические - нечеткие; с сосредоточенными параметрами - с распределенными; стационарные - нестационарные; линейные - нелинейные и т.д.

Кроме того, структура модели определяется также набором размерностей: количеством переменных (входа, выхода, состояния) и параметров.

Таблица 1

Математические модели систем

Статические	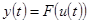Динамические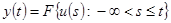
Дискретные (U, Y, Т - конечные (счетные) множества)	Непрерывные (U, Y, Т - континуумы)
Детерминированные	Стохастические, нечеткие
С сосредоточенными параметрами (конечные уравнения (т.е. алгебраические или трансцендентные), разностные уравнения, ОДУ)	С распределенными параметрами (уравнения с запаздыванием, в частных производных, интегральные уравнения)
Линейные	Нелинейные
Стационарные (параметры не меняются во времени)	Нестационарные (параметры изменяются во времени)

Остановимся на задаче выбора типа ММ. Прежде всего, следует дать краткую характеристику основным типам ММ.

Статические и динамические модели

Математическая модель системы называется статической, если значение выхода y(t) зависит от значения входа u(t) только в тот же момент времени t. Символически это свойство записывается так:

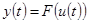, (1)

где F – символ некоторого преобразования (оператора).

Кроме явных функциональных зависимостей (1), статические модели могут задаваться неявно, в виде уравнения или системы:

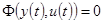. (2)

Так обычно записываются уравнения статических режимов радиоэлектронных схем, многих механических, энергетических систем и т.д. Уравнение (2) должно быть однозначно разрешимо относительно y(t).

Статическими моделями пользуются, когда в рамках поставленной задачи (с точки зрения достижения выбранной цели) инерционностью и «памятью» реальной системы можно пренебречь. Это возможно при выполнении ряда условий, в число которых входят следующие:

1) система устойчива, т.е. переходные процессы после скачкообразного изменения входов затухают. Конечное время затухания с заданной точностью обозначим через t_пер;

2) входы меняются медленно, т.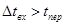е. где 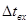- время между изменениями входных воздействий;

3) выходы измеряются редко, т.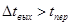е. где 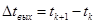- промежутки между измерениями входных величин.

В динамических моделях значение y(t) может зависеть от всего прошлого (предыстории) входного процесса:

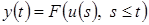(3)

Динамические модели позволяют учесть наличие «памяти», инерционности системы. Математическим аппаратом описания динамических систем являются дифференциальные, разностные уравнения, конечные автоматы, случайные процессы.