Степенное множество графа

Степенным множеством графа называется множество степеней его вершин. От степенной последовательности о множество отличается тем, что в нем не учитывается число вершин, имеющих заданную степень, тогда как в степенной последовательности каждое число фигурирует столько раз, степенью скольких вершин оно является.

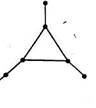Степенное множество графа G обозначим через S(G). Так, для графа G, изображенного на рис. 52.1, S(G) = = {1, 2, 3}.

Хотя степенная последовательность графа удовлетворяет определенным условиям, однако степенным множеством графа может быть произвольное множество. Об этом свидетельствует следующая

Теорема 52.1. Любое конечное множество S натуральных чисел является степенным множеством некоторого порогового графа. Минимальный порядок таких графов равен s +1, где s — максимальное число из множества S. Очевидно, что из этой теоремы вытекает

Следствие 52.2. Любое конечное множество целых, неотрицательных чисел является степенным множеством некоторого графа.

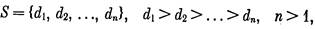Доказательство теоремы 52.1. Если S(G) = = S, то \G\ ≥ s+ 1, так что нужно только доказать существование подходящего графа G. Утверждение тривиально для одноэлементного множества S, поскольку S(K_n)={n — 1}. Пусть теперь

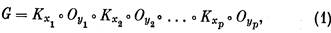и пусть, для определенности, п = 2р — четное число. Нужный граф будем искать в виде

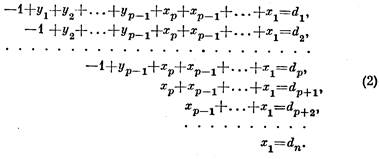
где К_Х°Н- граф, полученный из графа Н добавлением х доминирующих вершин, а О_У°Н — граф, полученный из графа Н добавлением у изолированных вершин. Любой граф вида (1) является пороговым. Попытаемся подобрать числа х_а и y_β в выражении (1) так, чтобы выполнялось - равенство S(G) = S. Для этого должно быть

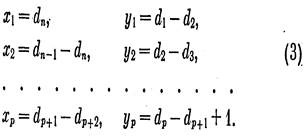Очевидно, что система уравнений (2) относительно неизвестных х_i, yj (i =1,p,j =1, р) имеет решение, все координаты которого положительны:

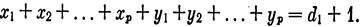Подставив в выражение (1) числа, определяемые равенствами (3), получим граф G, для которого S(G)=S. Число его вершин равно

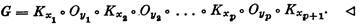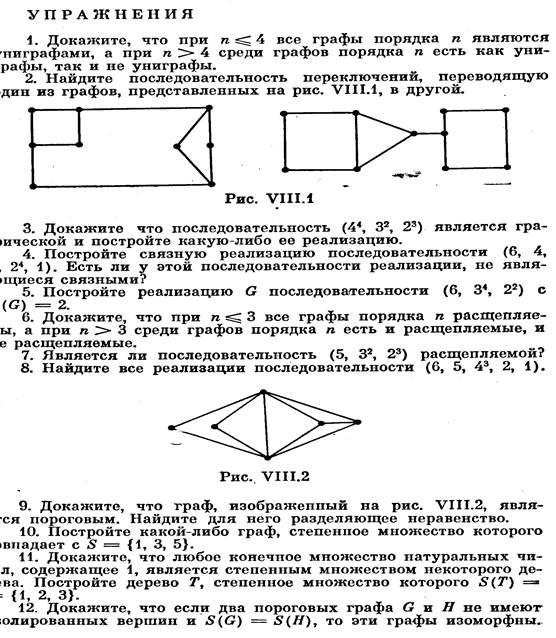
Для нечетного п = 2р + 1 построение аналогично, толь-to вместо формулы (1) используется формула

Дата добавления: 2019-07-26; просмотров: 924;