Числовые характеристики случайных величин
Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится пользоваться, так называемыми, числовыми характеристиками случайной величины. К ним относятся:
1.математическое ожидание M;
2.дисперсия D;
3.среднее квадратичное отклонение 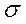 .
.
Математическое ожидание дискретной случайной величины X – это сумма произведений всех ее возможных значений 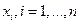 на их вероятности
на их вероятности 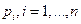 .
.
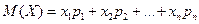
Математическое ожидание непрерывной случайной величины X, возможные значения которой принадлежат отрезку [a,b] – это определенный интеграл
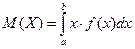
Математическое ожидание случайной величины (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина. Она характеризует среднее значение случайной величины.
Свойства математического ожидания:
1.M(C)=C – математическое ожидание константы равно самой константе
2. 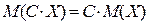
3. 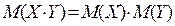
4.M(X+Y)=M(X)+M(Y)
Дисперсия и среднее квадратичное отклонение – это числовые характеристики случайной величины, которые позволяют оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания.
Отклонением называют разность между значением случайной величины и ее математическим ожиданием, т. е. 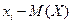
Пусть закон распределения дискретной случайной величины известен:
Так как одни возможные отклонения положительны, а другие отрицательны, то математическое ожидание отклонения обладает важным свойством:
M(X – M(X))=0, т.е. математическое ожидание отклонения всегда равно нулю.
Поэтому для оценки рассеяния случайной величины вокруг ее математического ожидания вычисляют квадрат отклонения случайной величины.
Дисперсией (рассеянием) случайной величины (как дискретной, так и непрерывной) называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Для дискретной случайной величины: D(X) = M(х – M(X))2
Для вычисления дисперсии часто бывает удобно пользоваться следующей формулой: D(X)=M(X2)–(M(X))2, т. е. дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.
Для непрерывной случайной величины:
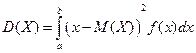
В последнем выражении все возможные значения случайной величины принадлежат отрезку (a, b).
Дисперсия случайной величины (как дискретной, так и случайной) есть неслучайная величина (постоянная величина).
Свойства дисперсии:
1. D (C) = 0
2. D (CX) = С2 D (X)
3. D (X+Y) = D (X) + D (Y),
4. D (C+X) = D (X),
5. D (X-Y) = D (X) – D (Y).
Пример:
Дискретная случайная величина задана законом распределения:
X 1 2 5
P 0,3 0,5 0,2
Математическое ожидание этой случайной величины равно:
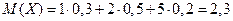
Закон распределения квадрата случайной величины, т. е. X2:
X2 1 4 25
P 0,3 0,5 0,2
Математическое ожидание X2 равно:
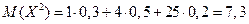
Тогда дисперсия приведенной случайной величины равна:
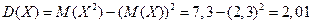
Среднее квадратичное отклонение:
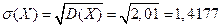 .
.
Свойство среднеквадратичного отклонения:
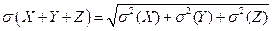
Рассмотрим пример, если задана непрерывная случайная величина.
Пусть непрерывная случайная величина задана интегральной функцией распределения:
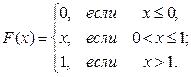
Найдем дифференциальную функцию распределения:
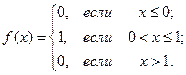
Математическое ожидание X и X2:
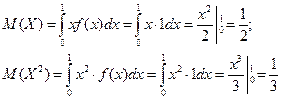
Тогда:
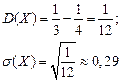
Если равномерно распределенная случайная величина задана в интервале [a,b], то ее математическое ожидание, дисперсия и среднее квадратичное отклонение равны:
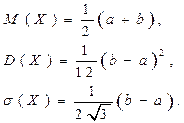
Дата добавления: 2017-02-20; просмотров: 891;
