ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
(ЗЛП)
ЗЛП – задача математического программирования с линейной целевой функцией и линейными ограничениями. Является наиболее изученной задачей мат. программирования. Обычно на практике возникает при решении задач, связанных с распределением ресурсов, планированием производства, организацией работы транспорта и т.п. ,т.к в этих случаях “расходы” и “доходы” ,как правило линейно(или близко к линейным) связаны с количеством затраченных средств (Напр. Стоимость партии товаров линейно зависит от их количества, оплата перевозок пропорциональна весу перевезенных грузов (или расстоянию и весу) и т.п.
__________________________________________________________________
Прим:
Предприятие производит выпуск изделий двух наименований U 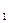 и U
и U 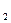 .
.
На изготовление изделий необходимо сырье 3-х видов - S 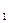 , S
, S 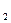 , S
, S 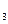 , причем
, причем
на изготовление единицы продукции 1-го вида необходимо соответственно
a 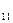 =1 ,a
=1 ,a 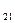 =2 , a
=2 , a 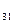 =2 единиц сырья, а на изготовление единицы продукции 2-го
=2 единиц сырья, а на изготовление единицы продукции 2-го
вида соответственно a 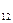 =1 , a
=1 , a 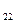 =5 , a
=5 , a 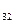 =2 единиц сырья.
=2 единиц сырья.
При реализации одного изделия 1-го вида приносит предприятию прибыль c 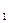 =3 ед. ,а 2-го вида - c
=3 ед. ,а 2-го вида - c 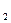 =4 ед.
=4 ед.
Необходимо так спланировать производство , т.е. определить объем выпуска изделий каждого вида, чтобы в рамках имеющихся ресурсов каждого вида
b 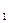 =8 ед. , b
=8 ед. , b 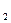 =30 ед. , b
=30 ед. , b 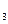 =14 ед. соответственно , обеспечить максимальную прибыль (доход).
=14 ед. соответственно , обеспечить максимальную прибыль (доход).
Формально задачу можно записать следующим образом:
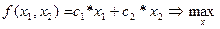 (
( 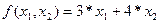 )
)
при ограничениях на ресурсы:
a 
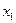 + a
+ a 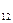
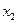
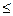 b
b 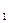 (
( 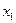 +
+ 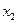
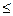 8)
8)
a 
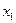 + a
+ a 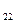
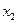
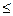 b
b 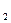 (2
(2 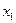 +5
+5 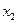
 30)
30)
a 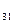
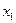 + a
+ a 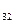
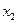
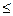 b
b 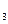 (2
(2 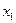 +
+ 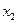
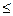 14)
14)
и на переменные 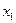
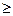 0 ,
0 , 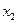
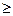 0;
0;
Кроме того могут быть ограничения на минимальные объем выпускной продукции каждого вида и т.д.
Как видим в нашем случае целевая функция и ограничения линейны, т.е. мы получим ЗЛП.
В общей постановке ЗЛП состоит в отыскании значений n переменных
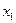 ,
, 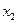 ,…,
,…, 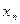 , доставляющих экстремум целевой функции
, доставляющих экстремум целевой функции
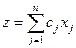
при ограничениях
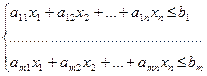
и 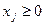
Система ограничений задает область допустимых решенийX. В общем случае она представляет собой выпуклый многогранник в n-мерном пространстве. Вершины его являются крайними точками и их число конечно.
В математике доказано, что решение ЗЛП ,если оно существует, всегда достигается хотя бы в одной крайней точке указанного многогранника.
На этом свойстве ЗЛП построены все методы её решения. Суть их заключается в организации перебора крайних точек таким образом, чтобы значение целевой функции при движении от точки к точке не уменьшалось.
Это обеспечивает поиск решения за ограниченное число шагов, исключая полный перебор всех крайних точек. (Напр. Симплекс-метод)
Существуют стандартные программы, реализующие методы решения ЗЛП.
Для того, чтобы ими воспользоваться, как правило, задачу необходимо привести т.н. и “стандартному” виду
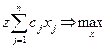
при ограничениях
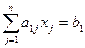
…………..
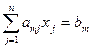
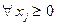
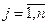
Переход от неравенств “ 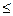 ” к равенству в ограничениях может быть осуществлен засчет введения дополнительных неотрицательных переменных, не входящих однако в целевую функцию. Напр.:
” к равенству в ограничениях может быть осуществлен засчет введения дополнительных неотрицательных переменных, не входящих однако в целевую функцию. Напр.:
для 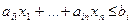 введем
введем 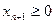 и получим
и получим
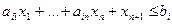
и так для каждого неравенства.
Это приводит к увеличению размерности задачи, но позволяет использовать стандартные методы её решения.
(Лит-ра Вагнер Г. ,Основы исследования операций ,М.Мир,197?,т.1
Тоха Х., Введение в исследование операций, М.Мир,1985 ,т.1 ).
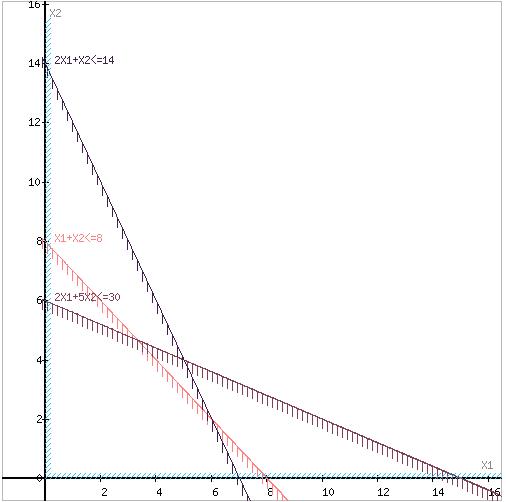
Для случаев 2-х переменных ЗЛП удобно решать графически. Так для рассмотренного выше примера при заданных значениях параметров получим:
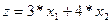
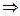 max
max
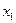 +
+ 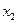
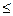 8 (1)
8 (1)
2 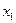 +5
+5 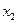
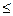 30 (2)
30 (2)
2 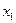 +
+ 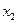
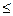 14 (3)
14 (3)
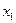 ,
, 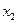
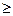 0
0
c 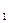 =3 ; c
=3 ; c 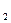 =4
=4
a 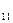 =1 ;a
=1 ;a 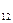 =1 ; b
=1 ; b 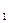 =8
=8
a 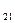 =2 ;a
=2 ;a 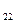 =5 ; b
=5 ; b 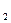 =30
=30
a 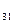 =2 ; a
=2 ; a 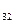 =2 ; b
=2 ; b 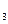 =14
=14
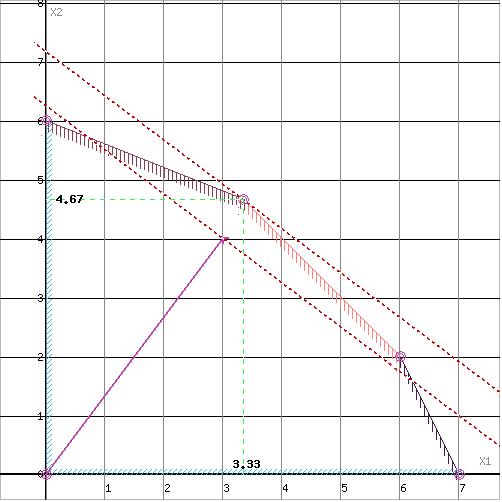
Решение: 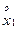 =
= 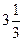
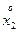 =
= 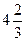
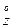 =
= 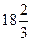
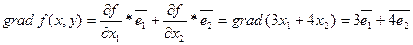
Найденное оптимальное решение ( 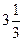 ;
; 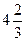 ) в общем случае может быть нецелочисленным. Однако в ряде задач это может быть неприемлемым из-за физической нереализуемости.
) в общем случае может быть нецелочисленным. Однако в ряде задач это может быть неприемлемым из-за физической нереализуемости.
В этом случае наряду с ограничениями неотрицательности переменных вводятся требования по их целочисленности, что значительно повышает сложность решения задачи, т.к. простое округление полученного решения до ближайших целых, как правило, не позволяет получить оптимального решения и, кроме того, может вывести его из области допустимых.(Округление допустимо лишь в тех случаях, когда не выводит из области допустимых и изменение целевой функции при отклонении решения от строго оптимального – не значительно ).
Существуют специальные методы решения целочисленных задач Л.П.
Напр. алгоритм Гомори, которые заключается с след-м:
На первом шаге отбрасывается требование целочисленности переменных и ищется оптимальное решение одним из общих методов. Найденное оптимальное решение проверяется на целочисленность и если оно удовлетворено, то задача решена.
В противном случае по определенному правилу, вводится дополнительное линейное ограничение, отсекающее найденное нецелочисленное из допустимой области и снова решается обычная ЗЛП. Новое оптимальное решение снова проверяется на целочисленность и т.д. до тех пор пока задача не будет решена.
Методы решения целочисленных задач линейного программирования как правило достаточно громоздки и требуют значительных затрат ?????тельных ресурсов.
Строго говоря, они относятся к классу нелинейных, хотя внешне очень схожи с линейными задачами.
Дата добавления: 2018-03-01; просмотров: 758;
